Декартово произведение множеств

 

Одним из важных понятий теории множеств является понятие декартова произведения множеств.

Декартовым произведением А×В множеств А и В называется множество М вида

М={(a_i,b_j):a_iÎA, b_jÎB}.

Здесь круглыми скобками () обозначается последовательность, т.е. множество, в котором зафиксирован порядок элементов (упорядоченное множество). Другое название такой последовательности – вектор (кортеж). Элементы, образующие вектор, называются координатами или компонентами, нумеруемыми слева направо. Векторы длины 2 часто называют упорядоченными парами, длины 3 – тройками и т.д. Вектор U длины n иногда называют n-кой («энкой»). Проекцией пр_iU вектора U называется его i-я компонента. Таким образом, М=А×В это множество пар.

В частности, если А=В, то обе координаты принадлежат одному множеству А² (В²).

Аналогично понятию декартова произведения двух множеств определяется декартово произведение n множеств:

 

 

Соответствия и функции

 

Соответствием между множествами А и В называется подмножество их декартова произведения GÍА·В.

Если (а,b)ÎG, то b соответствует а при соответствии G. Множество проекций пр₁G называется областью определения соответствия, множество пр₂G – областью значений соответствия. Если пр₂G=А, то соответствие полностью определенное (в противном случае – частичное). Если пр₂G=В, то соответствие сюрьективно.

Множество всех bÎВ, соответствующих элементу а, в А называется образом а в В при соответствии G. Множество всех а, которым соответствует b, называется прообразом b в А при соответствии G.

Всюду определенное соответствие называют отображением и иногда записывают как Г:ХaY, где a – знак отображения.

Подмножество FÌX·Y называется функцией, если для каждого элемента х, хÎХ найдется не более одного элемента yÎY в парах вида (х,y)ÎF. При этом, если для каждого элемента х имеется один элемент y, то функция полностью определена, в противном случае – частично определена (недоопределена). Множество Х – область определения функции F, множество Y – область значений функции. Часто вместо записи (х,y)ÎF используют запись y=F(х), при этом элемент х называют аргументом или переменной, а y – значением функции F. Количество аргументов определяет местность функции.

Сопоставим с декартовым произведением двух множеств прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения [9-10].

На рис. 7а изображено подмножество декартова произведения множеств Х={х₁,х₂,х₃,х₄} и Y={y₁,y₂,y₃}, не являющееся функцией, на рис. 7б – являющееся полностью определенной функцией; на рис. 7в – являющееся частично определенной функцией.

 

 

а) F1ÍX×Y, не являющееся функцией, т.к. одному значению х может соответствовать два значения y.

б) F2ÍX×Y, являющееся полностью определенной функцией.

в) F3ÍX×Y, являющееся недоопределенной функцией, не определенной на значении аргумента х3.

Рис.7. Подмножества декартова произведения X×Y

 

Соответствие G между множествами Х и Y называется взаимно однозначным, если каждому элементу хÎХ соответствует определенный элемент yÎY, и, наоборот, каждый элемент yÎY оказывается поставленным в соответствие одному элементу хÎХ.

Соответствие между множеством функций и множеством чисел называется функционалом [19]. Часто говорят «функционал качества».

Например, функционалом может быть определенный интеграл, ставящий в соответствие некоторой функции число.

Соответствие между двумя множествами функций называется оператором. Например, имеется оператордифференцирования.

Множество А называется эквивалентным множеству В, если существует взаимнооднозначное соответствие множеств А и В, это обозначается как

А=В или А~В.

Этот факт позволяет определять неизвестную мощность одних множеств по известной мощности других, им эквивалентным. Множества, эквивалентные (равномощные) множеству натуральных чисел, называются счетными. В счетных множествах возможна нумерация элементов. Пример множества, не являющегося счетным – множество всех действительных чисел отрезка [0,1]. Это доказывается теоремой Кантора [19]. Попробуем пронумеровать это множество. Расположим все числа, изображенные бесконечными десятичными дробями в порядке нумерации:

0, а₁₁ а₁₂ а₁₃...

0, а₂₁ а₂₂ а₂₃...

0, а₃₁ а₃₂ а₃₃...

......,

где первая цифра индекса – номер бесконечной десятичной дроби. Рассмотрим теперь любую бесконечную десятичную дробь 0, b₁ b₂ b₃... такую, что b₁¹а₁₁, b₂¹а₂₂, b₃¹а₃₃ и т.д. Такая дробь не входит в указанную последовательность, так как отличается от первого числа первой цифрой, от второго числа – второй цифрой и т.д. Следовательно, все числа из отрезка [0,1] не могут быть пронумерованы, т.е. это множество несчетно. Его мощность называется континуум и все эквивалентные ему множества называются континуальными. Так, множество всех подмножеств счетного множества континуально.

 

Отношения

 

Подмножество RÍMⁿ называется n местным отношением на множестве М. Говорят, что а₁,...,а_n находятся в отношении n, если (а₁,...а_n)ÎR. Одноместное отношение (свойство, признак) – это просто подмножество М. Наиболее часто встречающиеся и хорошо изученные – бинарные отношения, для них RÍM². Если а,b находятся в отношении R, то это часто записывают в виде аRb.

Примеры бинарных отношений на множестве людей «быть сыном», «служить в одном полку», «любить», «дружить».

Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде или отношение «ставить оценку», определяемое следующим образом: «преподаватель х ставит студенту y оценку z».

Можно определить обратное отношение R^-1. Например, для отношения £ обратным является отношение ³.

Рассмотрим свойства отношений.

Отношение R называется рефлексивным, если для любого аÎМ имеет место аRа. Отношение антирефлексивно, если ни для какого аÎМ не выполняется аRа.

Отношение £ рефлексивно, а отношение «быть сыном» антирефлексивно.

Таким образом, рефлексивность – свойство выполнимости отношения для каждого элемента подмножества R относительно самого себя.

Отношение R симметрично, если из aRb следует bRa (это может быть записано с использованием стрелки следования aRb®bRa). В противном случае отношение R несимметрично, то есть, если aRb истинно, то bRa ложно. Отношение R антисимметрично, если из a_iRa_j и a_jRa_i следует, что a_i=a_j.

Отношение дружбы симметрично. Отношение любви, как правило, несимметрично. Отношение £ антисимметрично, действительно, если а£b и b£а, то а=b. Отношение R симметрично тогда и только тогда, когда R=R^-1.

Отношение R транзитивно, если для любых а,b,с из аRb и bRс следует аRс. Это можно записать с использованием знака конъюнкции & (союз «И») и символа ® «следует»:

(аRb)&(bRс)®аRс

Например, отношение «являться начальником» транзитивно. Отношение дружбы нетранзитивно. Для любого отношения R отношение 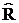, называемое транзитивным замыканием R, определяется следующим образом: а b, если существует цепочка из n элементов а=а₁,а₂,...,а_n-1,а_n=b, в которой между соседними элементами выполнено R:а₁Ra₂,a₂Ra₃,...,a_n-1Rb.

Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком», являющееся объединением отношений «быть сыном», «быть внуком», «быть правнуком» и т.д.

Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно.

Таково отношение равенства.

Отношение нестрогого порядка рефлексивно, антисимметрично и транзитивно.

Отношение строгого порядка антирефлексивно, антисимметрично и транзитивно.

Отношения £ и ³ для чисел – отношения нестрогого порядка, отношения <, > – отношения строгого порядка.

Пример лексико-графического упорядочения слов в словарях: лесáлето, где á – символ упорядочения.

Отношение доминирования (например, на множестве спортсменов или спортивных команд) обозначается >>. Это отношение антирефлексивно, несимметрично и нетранзитивно.

Отношения (relations) являются основным объектом современных систем управления реляционными базами данных (СУБД), в которых отношения задаются, как правило, на произведении различных множеств. В теории СУБД, в отличие от «академической» записи отношений, принятой в математике используется содержательные записи, например:

<Иван, Мария, цветы, восьмое марта> – четырехместное отношение «Дарить», <Профессор Иванов, студент Петров, отлично> – тернарное отношение «Ставить оценку».

Чаще всего отношения в СУБД задаются таблицами, столбцы которых называют также атрибутами, полями, а строки – кортежами, записями.

Реляционная база данных, то есть база данных, основанных на отношениях, представляет собой совокупность таблиц. Таблица состоит из строк и столбцов. Столбец, то есть поле, задается так называемыми реквизитами: именем, типом (числовой, признаковый и т.д.), длиной, точностью для числовых данных.

Запись, таким образом – это совокупность связанных полей. Таблица – совокупность записей одной структуры. Одно из полей является так называемым первичным ключём, значения которого однозначно указывает на соответствующие ему записи (отношения).