Изменение радиуса шаров и параметра g

В анимацию для корневого объекта добавлены заливка цветом пространства движения шаров, краткая информация о модели, слайдеры для изменения радиуса шаров и ускорения свободного падения, а также кнопки для изме­нения числа шаров. Рассмотрим возможность изменения радиуса шаров r во время работы модели. Если бы этот параметр был определен в классе Ball как Простой, то нам нужно было бы обращаться к нему из (анимации) класса Root только со ссылкой на конкретный экземпляр класса Ball. Для того чтобы сделать возможным изменение радиуса сразу всех шаров из вклю­чающего их объекта Root, можно применять разные способы. Один из са­мых простых использован здесь. Этот параметр у шара сделан глобальным (что в терминах языка Java называется статическим, то есть относящимся ко всему классу, а не к экземпляру класса). Это можно сделать, поскольку ра­диус шара в нашей модели не изменяется в каждом конкретном экземпляре класса Ball: он связан лишь с самим классом Ball. Для этого в окне свойств параметра r в активном объекте Ball установлен тип этого параметра

Глобальный (Global). Из активного объекта Root обращаться к этому пара­метру можно так: Ball.r. Именно это сделано в слайдере, изменяющем этот параметр. Полностью аналогично определен общий для всех шаров пара­метр д.

Динамическое изменение числа шаров

Работа с динамически изменяющимися массивами активных объектов описана в разд. 7.6. Там же определены операторы, которые нужно ис­пользовать для порождения нового объекта и для выбрасывания одного из существующих. Для исключения произвольного шара (элемента массива balls) из данной модели при ее функционировании мы можем использо­вать оператор:

if(balls.size()>0) dispose_balls(balls.random());

который сначала проверяет, есть ли в модели хотя бы один шар. Для вклю­чения в этот массив дополнительного шара (элемента класса Ball) при функционировании модели используется оператор:

setup_balls(new Ball(), 0);

Эти операторы введены в поле Реакция на событие окон свойств соответст­вующих кнопок анимации (—шар и +шар). Нажатие этих кнопок во время работы модели приведет к нужному эффекту (рис. 23.5).

Модель плоской кинематики

Это классическая задача кинематики: построить траекторию некоторой точ­ки системы из четырех стержней, в которой один стержень двигается вокруг своей неподвижной опоры.

Постановка задачи

Постановка задачи полностью определяется рис. 23.6. Необходимо постро­ить траекторию точки т жесткой системы, в которой стержень r2 двигается вокруг неподвижной опоры с постоянной угловой скоростью.

Исходные данные (параметры) задачи: r1=180, r2=90, rЗ=210, r4=120.

Одна из проблем, возникающих при исследовании этого механизма — при каких условиях (например, при какой длине стержня r4) стержень r2 может вращаться вокруг точки а без ограничений. Подобные проблемы именно для этой системы рассматриваются в курсе "Кинематика и динамика ма­шин" Университета Notre Dame в США: www.nd.edu/~stanisic/ME339/ grashoff. criterion. pdf.

Модель данной механической системы, разработанная в среде AnyLogic, представлена в проекте FourBarKinematics1. Она находится в папке Model Examples\Part V.

Уравнения

Координаты точек А, в, с, d и т легко выражаются через длины стержней и углы. Длины стержней в модели обозначаются rl, r2,... r4. Расположим точку а в начале координат. Тогда координаты точки в, очевидно, (r4,0), а остальные координаты:

xB=r2 *cos(phi2);            yB=r2*sin(phi2);

xC=rl+r4*cos(phi4);         yC=r4*sin(phi4);

xT=(xB+xC)/2;               yT=(yB+yC)/2.

Угол phi2 пусть растет с угловой скоростью 1 рад/с, т. е его можно опреде­лить так:

phi2=t.

Два других угла определятся из неявных уравнений:

xB+r3*cos(phi3) = xC; yB+r3*sin(phi3) = r4*sin(phi4).

Описание модели

Модель имеет только один активный объект, представляющий модель трех движущихся стержней, поэтому корневой объект Model является единствен­ным активным объектом нашей модели. В поле параметры окна свойств объекта Model определены четыре вещественных параметра r1=180, r2=90, rЗ=210, r4=120. В окне редактора структуры определены семь переменных с плавающей запятой: хв, ув, хс, ус, хт, ут, phi2, phi3, рhi4.

Угол phi2 определен формулой phi2=t, поскольку в нашей модели он изме­няется с угловой скоростью 1 рад/сек. Текущее время в формулах в AnyLogic задается переменной с предопределенным именем t. Поэтому в поле фор­мул для phi2 записано просто t.

Для того чтобы описать в AnyLogic ту переменную, которая задается уравне­нием неявным образом, следует записать в поле Уравнения окна Код актив­ного объекта Model это уравнение в приведенном виде так, чтобы в левой части его стоял 0, и записать ту переменную, которая этим уравнением оп­ределяется, в скобках после имени функции find. Например, для перемен­ной phi3, которая определяется из уравнения

xB+r3*cos(phi3)=xC

в две строки без точек с запятой записано следующее:

О = xB+r3*cos(phi3) - хС

find (phi3)

Аналогично определена переменная phi4.

В AnyLogic все неявные уравнения, определяющие группу переменных, со­бираются в одну систему, и перечисление тех переменных, которые должны определяться из этой системы, может быть задано либо несколькими стро­ками

find(x) find(у) find(z)

либо одной строкой

find(x,y,z)

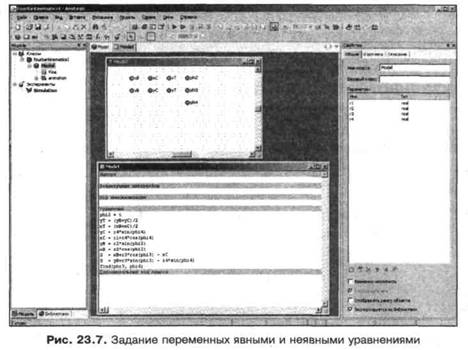
Именно так сделано при построении этой модели (рис. 23.7).

 

Запустив модель FourBarKinematics1 на выполнение, вы увидите следую­щую траекторию точки т — рис. 23.8.

23.4.3. Анимация работы трехзвенного механизма

Анимация по возможности должна представлять реальное поведение моде­лируемой системы. Анимированные модели выигрывают именно потому, что ожившее динамическое изображение способствует более глубокому по­ниманию сути моделируемых явлений. В данном проекте анимация состоит в оживлении рис. 23.6.

Отображение траектории точки при анимации. Ломаная линия

Отличие анимационной картинки от графика состоит в том, что движущие­ся объекты анимации не оставляют следов при движении. Если требуется отобразить траекторию движущегося объекта, это следует сделать явно при спецификации анимации. Это можно сделать, например, построив ломаную из нескольких точек, причем при каждом шаге перерисовывания выводимо­го изображения в окне анимации данная ломаная должна перерисовываться. Один конец введенной ломаной должен в каждый момент перерисовки изо­бражения принимать значения координат точки т с продвижением значений координат всех других точек.

В модели эта ломаная названа рь. Динамическое число точек ломаной рь задано параметром N. Точки ломаной определены так, что координаты X, У последней точки (ее номер равен N-1) принимают значения текущих коор­динат точки т на этом шаге (т. е. хт и ут), а каждая предыдущая (i-я) точка ломаной pL при каждом перерисовывании картинки продвигается на место последующей ((i+1)-й).

В AnyLogic значение координаты X точки с номером к у объекта рь можно получить, вызвав функцию pL.getPointx(k). Поэтому пересчет координат X ломаной pL в поле х[index] определяется следующим выражением языка Java:

index == N-1? xT: pL.getPointX(index +1)

а в поле Y[index] — выражением:

index == N-1? yT: pL.getPointY(index+1)

С моделью можно выполнить несколько экспериментов. Во-первых, можно изменять параметр r4 и наблюдать, как при этом меняется траектория точки T (рис. 23.9). Далее, можно изменять число точек ломаной рь, установив дру­гие значения параметра N.

Эту модель можно улучшить следующим образом. В тот момент модельного времени, когда с помощью слайдера значение параметра r4 изменится, со­берите все точки траектории, нарисованной в поле анимации, в точку T для того, чтобы старая траектория исчезла из поля анимации. Эта модель FourBarKinematics2 находится в папке Model Examples.

Точки траектории — это точки ломаной с именем рь, определенной в ани­мации. Ломаная является экземпляром класса shapePoly. В этом классе оп­ределено несколько методов. Все методы классов, которые используются в AnyLogic, перечислены в Справочнике классов, доступном при нажатии кнопки Справка главного меню. Один из методов этого класса, который можно найти в справочнике — метод setPoint, устанавливающий коорди­наты i-й точки ломаной.

У ломаной рь ровно N точек, которые нумеруются от о до n-1. Для того что­бы присвоить всем точкам ломаной рь значения координат точки т, в поле анимации в модели FourBarKinematics2 введена дополнительная кноп­ка с именем Сброс траектории, и в поле Реакция на событие окна свойств этой кнопки помещен код:

for(int i=0; i<N; i++) pL.setPoint(i, xT, yT);

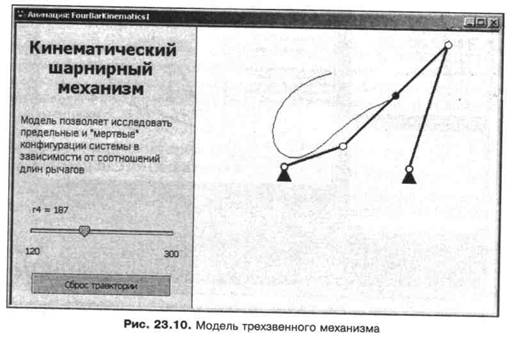
Любое нажатие кнопки Сброс траектории вызывает выполнение указанного цикла, что выражается в исчезновении нарисованной ранее траектории — все точки ломаной будут проецироваться в этот момент в точку т (рис. 23.10).

Заключение

Имитационные модели физических явлений, визуализирующие основные физические законы, позволяют обучаемому "играть" с моделью, изменяя ее параметры и наблюдая эффект. Это в сочетании с традиционными формами обучения может способствовать более эффективному изучению физики школьниками и студентами младших курсов.

Заключение

Имитационное моделирование существует, фактически, с момента появле­ния компьютеров. Вскоре после этого знаменательного события стали ясны огромные перспективы использования компьютера для проигрывания уп­рощенных описаний реальных процессов с целью изучения их поведения в различных возможных ситуациях. В настоящее время существует огромное число примеров успешного применения данного подхода. Уже сейчас в не­которых областях решения принимаются только после анализа их последст­вий на имитационных компьютерных моделях.

Однако широкому распространению имитационного моделирования до сих пор препятствует несколько причин. Во-первых, системы, для которых не­обходима разработка моделей, обычно сложны, что затрудняет построение для них моделей даже с использованием специализированных пакетов, под­держивающих процесс разработки моделей. Во-вторых, разработка сложных моделей часто требует от пользователя написания программного кода и зна­ния языка программирования, с которым совместима среда разработки. Традиционный подход в этой области основную проблему имитационного моделирования видел именно в разработке компьютерной програмы, реали­зующей модель, программ генерации и анализа случайных величин, про­грамм вывода и анализа результатов, а не в разработке и анализе модели как таковой. В результате разработка полезных моделей в традиционной техно­логии может тянуться годами. Например, в соответствии с [ЮР04] трудоем-, кость разработки сложных моделей составляет десятки человеко-лет. Оче­видно, что с течением десятилетий может умереть сама необходимость использования результатов анализа такой модели. Потому сроки разработки модели являются критическим фактором. Среда разработки имитационных моделей, скрывающая от разработчика все эти проблемы, может качествен­но ускорить построение и анализ имитационных моделей.

Удивительно, что революция, которая произошла за последние годы в об­ласти информационных технологий, почти не коснулась области имитаци­онного моделирования. Например, до сих пор студентов учат моделирова­нию на основе языка GPSS, изобретенного еще в 1962 году. В то же время

только аппаратная мощность современного ноутбука на несколько порядков превосходит мощность всей вычислительной техники, которая существовала в те годы в мире. Но главное даже не в ресурсных возможностях современ­ных компьютеров. В последние годы в области информационных техноло­гий разработаны мощные методы управления сложностью представления информации с помощью иерархии абстракций, появились новые идеи ин­теллектуализации интерфейса пользователя, новые методы задания систем как иерархии параллельно взаимодействующих процессов, представление информации с помощью анимации и динамической графики.

Не обязательно знать, как работает телевизор, чтобы его смотреть. Не нужно быть механиком, чтобы водить машину, не нужно знать структуру протоко­лов передачи данных, чтобы пользоваться Интернетом. В то же время мно­жество комментариев и советов в современных учебниках по теории и прак­тике имитационного моделирования посвящено таким проблемам, как управление памятью, манипуляциям с указателями, преобразованиям кален­даря событий модели. Но моделирование вовсе не требует умения организо­вать квазипараллелизм в имитационных системах, программно строить свя­занные списки, работать с календарем событий и многого другого, что ранее являлось обязательным в традиционной технике разработки моделей. Лозунг революции, которая уже происходит в имитационном моделировании, сле­дующий: "Не нужно быть ни профессиональным программистом, ни профессио­нальным математиком, чтобы разрабатывать имитационные модели". Это совсем не значит, что строить модели могут ничего не понимающие в про­граммировании и математике люди: создание полезных моделей требует подготовки в обеих этих областях.

Многочисленные примеры, приведенные в книге, показывают, что при разра­ботке модели с помощью AnyLogic от пользователя, фактически, не требуется знаний, не относящихся непосредственно к моделированию. Ему достаточно иметь только первоначальные знания о программировании. Для реализации и анализа стохастических имитационных моделей разработчик должен иметь лишь общие познания в статистике, но, например, ему не нужно самому реа-лизовывать генераторы случайных чисел — они уже реализованы в инстру­менте моделирования. Проведение эксперимента с моделью легко выполняет­ся на основе визуализации ее поведения и удобной интерпретации результатов. Поэтому автор надеется, что внедрение в практику разработки имитационных моделей программного инструмента AnyLogic положит начало революционным изменениям в этой области, к изменению понимания самого процесса моделирования. Эти изменения заключаются в переносе основной тяжести при разработке моделей с программирования на создание моделей, предоставляя разработчику модели удобный графический визуальный язык для выражения нужных абстракций и анализа модели, для управления про­цессом разработки модели. Все это, в конечном счете, должно привессти к существенному уменьшению трудоемкости создания моделей.

-

Литература

[АБ04] Борщев А. В. Практическое агентное моделирование и его место в ар­сенале аналитика //Exponenta Pro, N 3-4, 2004. (См. также http://www.gpss.ru/ index - h. html.)

[ЛК04] Лоу А. М., Кельтон В.Д. Имитационное моделирование. 3-е издание // СПб.: Питер, Киев: BHV, 2004. - 847 с.

[ЛК79] Клейнрок Л. Теория массового обслуживания // М.: Машинострое­ние. 1979. - 432 с.

[РП05] Пенроуз Р. Новый ум короля: О компьютерах, мышлении и законах физики // Пер. с англ. М.: Едиториал УРСС, 2005. — 400 с.

[РШ71] Шеннон Р. Имитационное моделирование систем — искусство и наука // М.: Мир, 1971. - 418 с.

[ЮР04] Рыжиков Ю. И. Имитационное моделирование. Теория и техноло­гия // СПб.: КОРОНА принт, 2004. - 384 с.

[ЮТ02] Толуев Ю. Записки симуляциониста, любящего и уважающего GPSS // http://www.gpss.ru/index-h.html, 2002.

[CS99] Standridge С. R. A Tutorial on Simulation in Health Care: Applications and Issues // Proceedings of the 1999 Winter Simulation Conference, 1999, http://www.wiiitersim.org/prog99.htm.

[EL63] Lorenz E. N. Deterministic nonperiodic flow. //J. Atmosf. Sci., 1963. — 20, 130-131 p.

[EM62] Moore E. F. Sequential Machines. Selected Papers //Reading, MA: Addison-Wesley, 1962.

[EX05] http://www.exponenta.ru/educat/class/courses/ode/themel7/theory.asp

[GB02] Buckner G. D. Simulink: A Graphical Tool for Dynamic System Simula­tion // Technical Report Dept of Mechanical and Aerospace Engineering North Carolina State University, 2002.

[GG62] Gordon G. A general purpose systems simulator // IBM Syst. J. 1962.

[JB98] Banks J., ed. Handbook of Simulation, Principles, Methodology, Advances, Applications, and Practice // J. Wiley & Sons, Inc., 1998. — 849 p.

[JF58] Forrester Jay W. Industrial Dynamics: a Major Breakthrough for Decision Makers // Harvard Business Rev., 1958.

[JF69] Forrester J. Urban Dynamics // Productivity Press, 1969.

[SR02] Sheldon M. Ross. Simulation // Academic Press, 3d edition, 2002. — 274 p.

[JS00] Sterman John D. Bysiness Dynamics. System Thinking and Modeling for a Complex World // Mc. Graw Hill, 2000. - 982 p.

[LM03] Laguna M., Marti R. The OptQuest Callable Library, in: Optimization Software Class Libraries, Voss S. and Woodruff D., eds. Kluwer Academic Publisher, Boston, 2003.

[MD71] Meadows, Donella, Dennis Meadows, Jorgen Randers, and William Behrens. The Limits to Growth. New York, NY: Universe Books, 1971. [MM71] Минский М. Вычисления и автоматы // M., Мир, 1971.

[PS93] Paich M., Sterman D. Boom, Bust, and Failures to Learn in Experimental Markets. // Management Science 39 (12) 1993, 1439—1458 p.

[RM00] Ritchie-Dunham J., Membrillo A. Breaking Down Functional Blinders: a Systematic View of the Organizational Map // Pegasus Communication. Systems Thinker, vol.10 No 10, Jan 2000.

[SM00] Schieritz N., Milling P. M. Modeling the Forest or Modeling the Trees. A Comparison of System Dynamics and Agent-Based Simulation.// Mannheim University, 2000.

[GL97] Glover F., Laguna M. Tabu Search. // Kluver Academic Publishers, Boston, 1997.

[JW54] Williams J. D. The Complete Strategist // McGraw Hill Book Co., 1954 (Русский перевод: Вильямс Дж. Д. Совершенный стратег или букварь по теории игр // М., Советское Радио, 1960).