Имитационная модель ограниченного маятника

Ограниченный маятник — это гибридная система, в которой происходят как непрерывное движение динамической системы, так и дискретные события, изменяющие сам характер движения. Поэтому модель системы включает описание как непрерывного движения (уравнения) так и дискретных собы­тий (стейтчарты).

Модель включает четыре переменные: х, у, alpha и omega, а также шесть параметров: L, 1, mu, alphaPin, g и alpha0. Смысл их всех очевиден (см. рис. 23.2), alphao — это начальное значение угла отклонения маятника. Основным компонентом модели для задания поведения ограниченного ма­ятника является стейтчарт с именем main. В этом стейтчарте два состояния, в одном состоянии описывается движение маятника на длинной нити (со­стояние long), в другом (состояние short) — движение с наличием ограни­чения. В этих состояниях различны определения угловой скорости и коор­динат центра маятника. Именно эти соотношения для угловой скорости и координат записываются в поле Уравнения окна свойств каждого из этих состояний. Уравнение

d(alpha)/dt = omega,

которое остается тем же самым в обоих случаях, определено для переменной alpha непосредственно в корневом объекте Model.

Условия перехода от одной модели поведения к другой определяются оче­видным образом. Пусть начальное положение маятника определяется его углом альфа0, который может принять значение от — до +альфа Pin. Маятник встре­чает препятствие (гвоздь), если он свободно движется против часовой стрелки (омега>о) и его отклонение от вертикали совпадает с углом альфа Pin или если он свободно движется по часовой стрелке и его отклонение меньше, чем -(2 — альфа Pin). Именно это и записано в условии перехода из состояния long в состояние short: (alpha >= alphaPin) && omega>0 || (alpha <= -(2*Math.PI-alphaPin) && omega <0)

Аналогично определяется условие перехода от движения с ограничением к свободному движению маятника.

При изменении длины нити маятника сохраняется его линейная скорость, значит, угловая скорость должна изменяться обратно пропорционально

изменению длины нити. Это записано в поле Действие окна свойств пере­ходов стейтчарта.

Анимация

Анимация в этой модели построена так же, как и в модели Pendulum. Коор­динаты (x,Y) шпильки определены так:

X: L*Math.sin(alphaPin) У: L*Math.cos(alphaPin)

Использование вместо sin и cos при вызове этих функций Math.sin и Math.cos объясняется тем, что sin и cos — в действительности, функции библиотеки Math компилятора Java, и написание их без указания имени библиотеки возможно только в поле Уравнения окна свойств переменной редактора AnyLogic. При компиляции программы на Java по построенной модели к именам математических функций, встретившимся в выражениях в поле Уравнения, имя Math добавляется компилятором автоматически.

23.3. Броуновское движение (Billiard _ Ba! ls)

Эта простая динамическая система имитирует столкновения биллиардных шаров, падающих и сталкивающихся мячей, воздушных шаров или частиц при хаотичном броуновском движении. Модель имитирует очевидное явле­ние, и она интересна не этим, а тем, как логика взаимодействия объектов модели может быть выражена с помощью языка Java. Модель с именем Billiard_Balls находится в папке Model Examples\Part V.

Постановка проблемы

Одинаковые по размеру и массе шары двигаются в ограниченном двумер­ном пространстве (камере) без потери энергии с упругим соударением.

Рисунок 23.3 показывает примеры столкновений шара с препятствием. Если препятствие — горизонтальная либо вертикальная стенка, то новое значение скорости шара получить легко: соответствующая составляющая скорости шара изменяет свое направление. Если препятствием является другой шар, то при центральном упругом столкновении таких шаров они просто обме­ниваются скоростями. Мы предполагаем в нашей модели, что силы трения очень малы по сравнению с упругими силами. Поэтому при нецентральном столкновении действием сил трения можно пренебречь. Соединим центры масс сталкивающихся шаров прямой и разложим скорость каждого шара на нормальную составляющую, направленную вдоль линии центров двух ша­ров, и составляющую, перпендикулярную к ней. Поскольку силы трения отсутствуют, изменяться будут только нормальные составляющие скорости шаров (vr) так же, как при центральном столкновении, т. е. при упругом столкновении шары с одной массой обмениваются нормальными состав­ляющими скоростей (рис. 23.3).

Модель

Модель содержит два активных объекта. Один активный объект — шар, дви­гающийся в ограниченном двумерном пространстве и сталкивающийся с другими шарами. Другой — это корневой активный объект Root, вклю­чающий массив таких шаров.

Модель шара

Шар моделируется активным объектом Ball, который имеет семь парамет­ров, Xmах и Ymax — это максимальные координаты двумерной прямоуголь­ной области, в которой двигаются шары, v — начальная скорость шара, r — радиус шара. Параметры r иgу шара определены как глобальные (в терми­нах языка Java статические), то есть относящиеся ко всему классу шаров, а не к каждому шару (экземпляру класса). Эти параметры мы будем изме­нять в экспериментах с моделью из корневого объекта.

Кроме того, для активного объекта Ball определен дополнительный дина­мический параметр целого типа с, принимающий в качестве значения ре­зультат вычисления функции uniform_discr(255). Если параметр динами­ческий, то при каждом его использовании он перевычисляется. Таким образом, каждый раз при использовании с этот параметр будет принимать случайное целое значение, распределенное равномерно между 0 и 255. К динамическому параметру с нужно обращаться так: с (). Еще один пара­метр color типа color имеет значение: new Color(с(), с(), с())

Каждый раз при его использовании конструктор

new Color(с(), с(), с())

будет порождать значение случайного цвета.

Модель шара имеет четыре вещественных переменных: положение его цен­тра х и у в координатах X и У, и составляющие скорости vx и vy по этим координатам (см. рис. 23.3). Координаты являются интегралами от соответ­ствующих скоростей:

d(x)/dt = vx d(y)/dt = vy

Производная от вертикальной скорости определена как ускорение свобод­ного падения g, направленное вниз:

d(vy)/dt = -g

В активном объекте Ball определена также еще одна переменная owner типа Root. Присваивание ей начального значения

(Root)getOwner()

даст указатель на корневой объект. Это означает, что в активном объекте Ball мы можем обращаться к любым объектам корневого класса Root.

Поведение шара

Поведение шара — это свободное движение, определяемое скоростями vx и vy. Шар свободно движется до тех пор, пока не столкнется с препятствием. Препятствия могут быть трех видов: вертикальная граница области, в кото­рой движутся шары, горизонтальная граница и, наконец, другой шар. При столкновениях скорости шаров меняются в соответствии с рис. 23.3. Столк­новение с препятствием — это событие, которое может отслеживаться с по­мощью стейтчарта. Стейтчарт (рис. 23.4) имеет одно состояние, которое от­ражает свободное движение шара, и три перехода, по одному на каждый из типов событий.

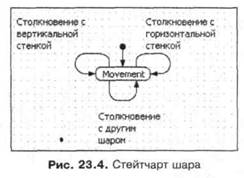
Переходы, моделирующие столкновение с границами области, очевидны. Столкновение с границей произойдет, если центр шара (с координатами х, у) приблизился к ней на расстояние радиуса r и шар движется в направлении этой границы. Изменение знака соответствующей составляющей скорости

при наступлении события столкновения с границей моделирует результат упругого отталкивания от нее.

Условие столкновения данного шара с другим шаром проверяется функцией checkHit (), которая возвращает указатель на тот шар, с которым столкнулся данный шар. Если столкновения не было, функция возвратит пустой указа­тель null. Эта функция определена в окне Код активного объекта Ball. Ес­ли столкновение произошло, то скорости vx и vy данного шара и того шара, с которым произошло столкновение, пересчитываются в поле Действие окна свойств соответствующего перехода стейтчарта.

Дополнительный код

Окно Код активного объекта Ball содержит фрагменты программного кода на языке Java, которые необходимы для описания алгоритмической части модели. Поле Уравнения этого окна содержит те соотношения, которые описаны при определении связей переменных модели. Поле Дополнительный код класса содержит определение дополнительных переменных и функций (методов в терминах языка Java) для данного класса. Здесь определены две переменные, m и color, а также функция checkHit о, возвращающая указа­тель на тот шар, с которым сталкивается данный. Поэтому эта функция имеет тип Ball.

У функции checkHit () есть единственный оператор

return (owner.Check (this));

являющийся просто вызовом функции check о в классе Root, возвращаю­щей нам тот шар, с которым при движении данный шар может столкнуться. В качестве параметра функции check о передается указатель this на дан­ный шар. В данном шаре ссылка на него же хранится в переменной this (см. разд. 7.7). Очевидно, что в рамках определения класса Ball мы не мо­жем определить функцию check (), поскольку она должна иметь информа­цию о положении и скоростях всего множества шаров, а это множество оп­ределено не в классе Ball, описывающем шар, а в активном объекте Root.

Поле Код инициализации окна Код активного объекта Ball содержит опера­ции, которые необходимо выполнить при порождении каждого экземпляра шара. Это задание случайного направления движения любого порождаемого шара (новый шар будет двигаться со скоростью v в случайно выбранном направлении), а также случайные значения координат его центра (распреде­ленные равномерно в заданном пространстве так, чтобы не попасть на уже имеющиеся в этом поле шары): do {

x=uniform(r, Xmax-r);

y=uniform(r, Ymax-r); } while (CheckHit()!= null);

Модель корневого объекта

Эта модель очень проста. Она включает массив объектов типа Ball (их чис­ло установлено 10) и не имеет ни своих переменных, ни параметров. В окне Код в поле Дополнительный код класса определена только функция check () типа Ball, возвращающая указатель на тот шар, с которым сталкивается шар b, переданный ей как параметр. В случае если столкновения нет, функция воз­вращает пустой указатель.

Анимация

Для каждого шара анимация определена следующим образом. Шар пред­ставляется кругом с динамическим значением r радиуса (и, следовательно, радиус шара будет изменяться в процессе работы модели, если будет ме­няться r). Значения динамических координат круга определено переменны­ми х и у (т. е. положение шаров в анимации определено их координатами), а динамическое значение цвета заливки круга и линии заданы параметром color, который при порождении шара принимает случайное значение цвета.

Анимация корневого объекта автоматически включает анимацию всех ша­ров, что означает, что порожденные экземпляры кругов (их начальное число 10) радиуса r со случайными начальными координатами, случайным направле­нием движения и случайно выбранным цветом будут двигаться, сталкиваясь, в прямоугольном пространстве, ограниченном размерами по оси X от 0 до Xmах и по оси Y от 0 до Ymах, имитируя движения соответствующих ша­ров в модели.