У проецирующих прямых одна из проекций вырождается в точку, а вторая проекция видна в натуральную величину (Н.В.) в виде прямой, перпендикулярной оси чертежа.
Прямые перпендикулярные горизонтальной плоскости проекций называются горизонтально проецирующими прямыми (рис.2.3, а).
Прямые перпендикулярные фронтальной плоскости проекций называются фронтально проецирующими прямыми (рис.2.3, б).
Точки, лежащие на одном проецирующем луче, называются конкурирующими относительно соответствующей плоскости проекций:
- точки А и В конкурируют относительно пл. P 1 (рис.2.3, а);
- точки C и D конкурируют относительно P 2 (рис.2.3, б) .
У проецирующих плоскостей одна проекция вырождается в прямую (след плоскости).
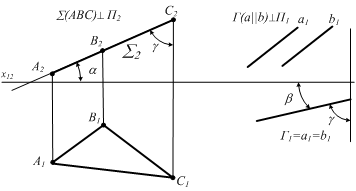
Плоскости перпендикулярные горизонтальной плоскости проекций называются горизонтально проецирующими плоскостями (рис.2.4, б).
Плоскости перпендикулярные фронтальной плоскости проекций называются фронтально проецирующими плоскостями (рис.2.4, а).

а) б) а) б)
Рисунок 2.3 Рисунок 2.4
Прямые, лежащие в одной проецирующей плоскости, называются конкурирующими прямыми, например, прямые АВ и ВС (на рисунке 2.4,а) или прямые а и в (на рисунке 2.4,б).
На комплексном чертеже у проецирующих плоскостей сразу определяются углы наклона к плоскостям проекций a, b, g (рис.2.4).
Прямые и плоскости параллельные плоскостям проекций - прямые и плоскости уровня (рис. 2.5 и рис.2.6).
| h – горизонталь h2 || x12 | A1B1 | = | AB | | f – фронталь f 1 || x12 | C2D2 | = | CD | |
|
| |
а) б)
Рисунок 2.5 Прямые уровня
Прямая параллельная горизонтальной плоскости проекций называется горизонтальной прямой или горизонталью h (рис. 2.5, а).
Прямая параллельная фронтальной плоскости проекций называется фронтальной прямой или фронталью f (рис. 2.5, б).
У прямых уровня на комплексном чертеже одна проекция параллельна оси чертежа, другая проецируется в Н.В., при этом сразу определяются углы наклона к плоскостям проекций a, b, g (рис.2.5).
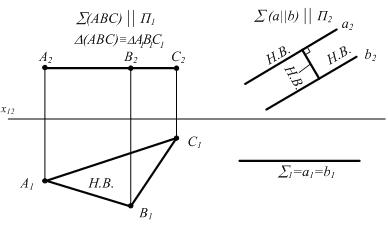
Плоскость параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью (рис. 2.6, а).
Плоскость параллельная фронтальной плоскости проекций, называется фронтальной плоскостью (рис. 2.6, б).
а) б)
Рисунок 2.6 Плоскости уровня
У плоскостей уровня одна проекция вырождается в линию, параллельную оси чертежа, другая проецируется в Н.В. Геометрические фигуры, лежащие в плоскостях уровня (параллельных плоскостям проекций), проецируются без искажения на плоскость проекций, которой они параллельны (рис.2.6).
Прямая или плоскость параллельная профильной плоскости проекций называется профильной прямой или плоскостью.
Для построения чертежа профильной прямой необходимо использовать трехкартинный эпюр (рис.2.7).

Рисунок 2.7







