Напомним, что фазово-модулированный сигнал (ФМ) определяется как
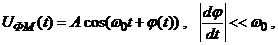
(3.47)
где последнее неравенство означает, что фаза ФМ сигнала меняется медленно.
Рассмотрим простейший пример ФМ сигнала:
(3.48)
Здесь m – коэффициент фазовой модуляции.
Покажем, что спектр ФМ сигнала (3.48) шире аналогичного АМ сигнала (3.45) и содержит не только составляющие ω 0 ± Ω, но и комбинации ω 0 ± 2 Ω, ω 0 ± 3 Ω, ω 0 ± 4 Ω... Для этого запишем ФМ сигнал (3.48) в комплексной форме и воспользуемся формулой из теории Бесселевых функций:
(3.49)
Из последнего равенства видно, что в спектре ФМ сигнала присутствует бесконечное число спектральных составляющих с частотами ω 0 ± k Ω (k – целое).
Рассмотрим случай малого коэффициента модуляции: m << 1. Тогда косинус и синус малого угла в (3.48) (m sin Ωt) можно разложить в ряд и удержать только члены, пропорциональные m и m 2.
см. справочный лист в конце.
Это в комплексной форме, см. рис. 3.29Б. Формула пригодится чуть позже.
(3.50)
Рис. 3.29.
А – спектр ФМ сигнала при m << 1.
Б – векторная диаграмма этого сигнала.
Если пренебречь малыми членами порядка m 2, то мы увидим, что в линейном по m приближении ФМ сигнал представляет собой сумму трёх спектральных составляющих.
На рис. 3.29 представлен спектр сигнала (3.50), состоящий из трёх составляющих. Там же представлена векторная диаграмма (справа): вектор 
основного колебания вращается с частотой ω 0 и две спектральные составляющие, вращающиеся с частотами ω 0 ± Ω. Относительно вектора основного колебания гармоники вращаются с частотами ± Ω так, что вектор их суммы всегда перпендикулярен вектору 
, так как несущая ~ + Re, а сумма боковых ~ – Im!
Из (3.50) также следует, что в приближении (m << 1), учитывающем члены ~ m2, в спектре фазово-модулированного сигнала появляются слабые гармоники ω 0 ± 2 Ω. Можно показать, что учёт членов ~ m3 приведёт к появлению гармоник ω 0 ± 3 Ω и т.д. Таким образом, мы приходим к выводу, что спектр ФМ сигнала шире спектра АМ сигнала, поскольку он дополнительно содержит гармоники ω 0 ± 2 Ω, ω 0 ± 3 Ω и так далее.
Рис. 3.30А.
Амплитуды гармоник фазово-модулированного сигнала с большими коэффициентами модуляции. При m = 1 появляется небольшая вторая боковая гармоника, при m = 2 появляется третья гармоника, а при m = 3 вторая гармоника становится больше первой. Ширина спектра растёт с ростом m.
Рис. 3.30Б.
Графики функций Бесселя
J0(z), J1(z), и J2(z).
Программа:
clc; AA = axes; set(AA, 'FontSize',18);
FigureColor=[1,1,1]; hFigure=gcf;
set(hFigure, 'Color', FigureColor)
z=[0:.01:20]; grid on; hold on;
y=besselj(0, z); plot(z, y,'r-', 'LineWidth',2);
y=besselj(1, z); plot(z, y,'b-', 'LineWidth',2);
y=besselj(2, z); plot(z, y,'k-', 'LineWidth',2);
