Свободные колебания в последовательном контуре

Рассмотрим свободные колебания в последовательном контуре, изображённом на рис. 2.19. Первоначально конденсатор заряжен до напряжения U₀. При замыкании цепи конденсатор начнёт разряжаться, при этом возникает переменный ток I(t). Напряжения на индуктивности L, конденсаторе C и сопротивлении r будут:

 

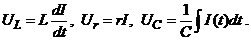
Рис. 2.19.

Последовательный колебательный контур. Первоначально конденсатор заряжен до напряжения U₀. После замыкания ключа в контуре возникают свободные колебания. Возможные типы колебаний будут показаны на рис. 2.20.

 

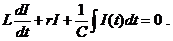По правилу Кирхгофа сумма напряжений равна нулю.

 

Продифференцировав по времени, получим:

                                   или                                                                                          (2.34)

 

где                 δ – коэффициент затухания, а                  – круговая частота колебаний в

контуре без потерь, то есть при  = 0.

Будем искать решение в виде I (t) = A e ^iωt. Подставив это решение в (2.34), получим характеристический многочлен:

                                                           

 

 

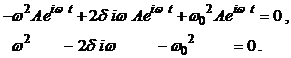
Вот здесь нам и пригодилась экспоненциальная форма записи переменного тока. Если бы ток (заряд, напряжение) были синусоидальными, то во втором члене был бы косинус, и он бы не сократился! Кстати, если в показателе экспоненты не ставить i, то частота всё равно может получиться комплексной.

Решая это квадратное уравнение и используя начальные условия, получим:

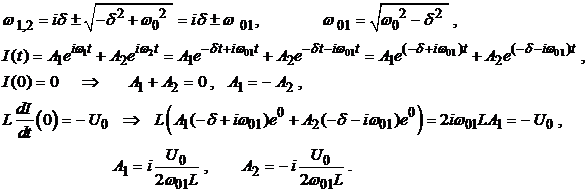
                                                            где

 

то есть  

 

 

При наших начальных условиях, ток в контуре будет:

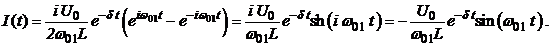
                                                                                                                                           (2.35)

 

Характер колебаний определяется величиной 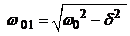. При отсутствии потерь δ = 0 и в контуре возникают незатухающие синусоидальные колебания вида:

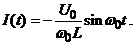
Напряжения на конденсаторе и индуктивности будут противофазны и равны по амплитуде. Их сумма в контуре без затухания будет всегда равна нулю!

 

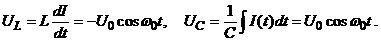
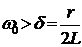Напряжения на конденсаторе и на индуктивности сдвинуты относительно тока на  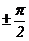, поэтому, когда ток через индуктивность максимален, напряжение на конденсаторе равно нулю. Максимум энергии магнитного поля катушки совпадает с нулём энергии электрического поля конденсатора и наоборот.

Если сопротивление всё же есть, но                   или                         ,                     , то:

 

 

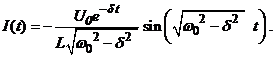
                                                                                                                                           (2.36)

 

Если δ > ω ₀, то: 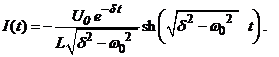                                             (2.37)

Существует решение и при ω₀ = δ.  Это решение есть предел, к которому стремятся (2.36) и (2.37) при 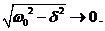 По правилу Лопиталя производные от числителя и знаменателя в (2.36) дадут 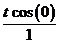, и в этом критическом случае ток будет  

 

 

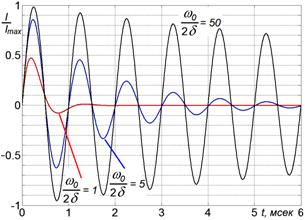
Рис. 2.20.Собственные колебания в последовательном контуре при разных значениях затухания.  , f = 1 кГц, ω ₀ = 6280 рад/сек.

 

В этом конспекте все графики сосчитаны (кроме экспериментальных!) и почти все начерчены в MATLABe. Кроме рис. 3.21-3.22, для которых применяли программу Cool Edit и рис. 4.12 и далее, для которых использовали виртуальные схемы и измерительные приборы из программы TINA.