Похожая на предыдущую схема (рис. 4.11) может быть использована и для детектирования АМ сигнала.
НЧ фильтр
Рис. 4.11. Схема детектирования АМ сигнала (слева) и спектры входного и выходного сигнала (справа).
Пусть входное напряжение есть амплитудно-модулированный сигнал:
(4.4)
Нашей задачей является выделение сигнала модуляции на частоте Ω. Обычно Ω << ω 0. Пусть опять ВАХ нелинейного сопротивления описывается формулой I = S1 U + S2 U 2 . Это приблизительно соответствует ВАХ германиевого диода для малых токов. Для упрощения выкладок примем также, что RНАГР << RНЕЛИН, а m << 1.
Тогда для выходного напряжения получаем:
 | |||
 | |||
мал по сравнению
с предыдущими
Оставим только члены с низкой частотой: (4.5)
Мы видим, что в спектре выходного сигнала присутствует нужная нам частота Ω, сигнал на которой нужно затем отфильтровать. После фильтра мы получим:
после фильтра (4.6)
Полезно сравнить спектры входного и выходного сигналов, приведённые на рис. 4.11 справа. Мы видим, что три частоты (ω 0, ω 0 ± Ω) во входном напряжении превращаются в три “набора”: (0, Ω, 2 Ω), (ω 0, ω 0 ± Ω), (2 ω 0, 2 ω 0 ± Ω, 2 ω 0 ± 2 Ω). Если ВАХ диода описывается более сложной функцией, содержащей и другие члены типа S3U3 + S4U4 +..., то добавятся и “наборы” вида: (3 ω 0, 3 ω 0 ± Ω, 3 ω 0 ± 2 Ω, 3 ω 0 ± 3 Ω).
Подчеркнём, что именно наличие нелинейного элемента приводит к такому умножению частот.
Фазовое детектирование
Пусть входное ФМ напряжение имеет вид UВХ (t) = U0 cos (ω 0 t + sin φ(t)), где в величине φ(t) записана информация. Будем считать, что φ(t) << 1 и sin φ(t) ≈ φ(t).
Тогда UBX (t) = U0 ( cos φ cos ω 0 t – sin φ sin ω 0 t).
Принцип детектирования ФМ сигнала заключается в том, чтобы до детектирования сначала превратить ФМ сигнал в АМ сигнал, который потом детектировать уже известным нам способом. Для превращения ФМ в АМ к ФМ сигналу добавляют опорное напряжение на частоте несущей. Фаза опорного напряжения должна быть выбрана оптимальным образом – это показано на фазовой диаграмме на рис. 4.12.
Главное, чтобы UОП = – 
. Здесь U1 – довольно произвольное напряжение. Важно только, чтобы оно было сдвинуто по фазе относительно U0 cos ω 0 t на ± π/2, то есть была синусоидой, а не косинусоидой. Модулирующее напряжение, в отличие от амплитудной модуляции, перпендикулярно вектору несущей (см. рис. 4.12, а также запись в комплексной форме в (3.50)). Вектор не стоит на месте, а крутится с частотой ω0, при этом он медленно и гармонически замедляет и ускоряет скорость вращения как d φ/ dt.
Принципиальная схема фазового детектора приведена на том же рисунке.
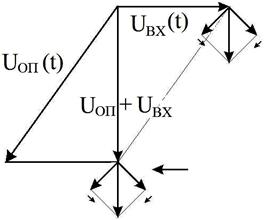
Рис. 4.12.
Фазовая диаграмма, показывающая, что сумма ФМ сигнала и опорного напряжения может быть АМ сигналом (при правильно подобранной фазе опорного напряжения). Входной сигнал состоит из суммы несущей и двух маленьких векторов, вращающихся в противоположных направлениях с низкой модулирующей частотой.
+
Это – амплитудная модуляция.
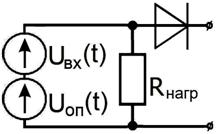
Рис. 4.13.
Принципиальная схема простейшего фазового детектора.
Опишем эту ситуацию подробнее:
входное опорное
Это – амплитудная модуляция! (4.7)
Мы видим, что эта сумма напряжений имеет вид АМ сигнала, который для детектирования можно подать на вход детектора. Фаза опорного напряжения определяется соотношением между U0 и U1.
Рис. 4.14.
Принципиальная схема балансного фазового детектора.
Иногда применяют схему балансного фазового детектора, изображённую на рис. 4.14. Важно, чтобы оба плеча балансного детектора были идентичны друг другу. В этой схеме на вход каждого детектора подаются напряжения U BX .
UА0 = UОП – UВХ , UB0 = UОП + UВХ,
UОП = U1 cos(ω 0 t + θ), UВХ (t) = U0 cos (ω 0 t + φ(t)).
Здесь θ – фаза опорного колебания. Пусть детекторы квадратичные, т.е. токи в детекторах пропорциональны квадрату напряжения. Тогда на выходе мы получим напряжение пропорциональное разности квадратов напряжений (UB0 2 – UA0 2):
(4.8)
НЧ вторая гармоника несущей
Если то после фильтрации низкочастотного сигнала:
Частотное детектирование
Представим частотно-модулированный сигнал в виде
U(t) = U0 sin {( 1 + m sin Ω t) ω 0 t}. (4.9)
Он может быть преобразован в АМ сигнал пропусканием через линейную цепь, коэффициент передачи которой имеет частотную зависимость. Например, для этого можно использовать резонансный контур, настраивая несущую частоту ω 0 на склон резонансной кривой контура (см. рис. 4.15). В тот момент, когда частота модулированного сигнала низкая, мы попадаем в точку А резонансной кривой (рис. 4.15), и амплитуда выходного сигнала минимальная. В точке, где частота большая (В, рис. 4.15), амплитуда выходного сигнала максимальная. Если этот сигнал продетектировать, то мы получим низкочастотный сигнал, пропорциональный sin Ω t (рис. 4.15).
Рис. 4.15. Детектирование частотно-модулированного сигнала.
Синхронное детектирование
Для детектирования не обязательно использовать пассивные нелинейные элементы. Вместо этого может быть использовано сопротивление, величина которого модулируется с частотой несущей. В качестве примера рассмотрим схему на рис. 4.16.
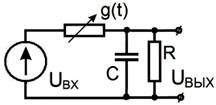
Рис. 4.16. Синхронное детектирование.
Пусть UBX (t) = Um (t) cos (ω t + φ(t)).
Проводимость g(t) = g0 + g1 cos(ω t+ γ). Потребуем, чтобы R и , то есть
проводимость достаточно мала, и большая часть входного напряжения падает на ней. Тогда ток определяется формулой:
(4.10)
несущая вторая гармоника НЧ составляющая
при
Мы видим, что ток содержит медленную составляющую, что и означает детектирование. Эта медленная составляющая отделяется от высокочастотных составляющих с помощью простейшего RC-фильтра.
Синхронный детектор может применяться для детектирования как ЧМ, так и АМ сигналов.
