9.1 Проектирование систем вентиляции
. Неотъемлемой частью всякого здания, предназначенного для трудовой деятельности и отдыха человека, являются устройства, создающие благоприятный внутренний климат. К таким устройствам относятся системы отопления (охлаждения) и вентиляции с соответствующим тепло – и холодоснабжением. Системой вентиляции называется совокупность устройств, обеспечивающих необходимое состояние воздушной среды в помещении или здании и исключающих загрязнение наружного воздуха выбросами из зданий. Воздух внутри помещения не должен иметь загрязнения пылью, вредными газами и парами, их содержание не должно превышать допустимых концентраций. Для достижения указанных условий воздушной среды в помещении устраивается вентиляция для удаления загрязненного воздуха и замены его чистым.
В зависимости от способа движения воздуха в вентилируемых помещениях вентиляция может быть естественной – за счет разности температур наружного и внутреннего воздуха и действия ветра и механическая – с искусственным побуждением движения воздуха за счет работы вентиляторов.
Рис. 2.1.5. Устройство вентиляции жилого дома
а) схема устройства вентиляции: I – с вертикальным сборным каналом, II – с горизонтальным сборным каналом; б) устройство вентиляционного канала приставного из шлакогипсовых плит; в) дефлектор.
Естественная вентиляция помещений может быть неорганизованной (инфильтрация через неплотности ограждающих конструкций) и организованной – с движением воздуха по каналам. Естественное движение воздуха по каналам происходит за счет гравитационных (весовых) сил, возникающих при разности объемных весов наружного и внутреннего воздуха помещений. На этом принципе основана вытяжная канальная вентиляция жилых помещений. При этом вытяжные каналы устраивают во внутренних кирпичных стенах или в виде приставных коробок (рис. 2.1.5б). На рис. 2.1.5а показана схема устройства вентиляции в девятиэтажном жилом доме. Согласно этой схеме, устраиваются сборные каналы, куда подключаются вертикальные каналы из каждого этажа (с перепуском через два этажа) или объединяются вентиляционные каналы из каждых 4-6 этажей в один сборный магистральный канал, выведенный до верха здания. Для увеличения напора верхняя часть магистрального канала снабжается дефлектором (рис. 2.1.5в), что позволяет дополнительно к гравитационному напору использовать напор, создаваемый дефлектором за счет силы ветра.
9.2 Проектирование систем теплоснабжения и водоснабжения
Системами теплоснабжения называется комплекс инженерных сооружений и устройств, служащих для выработки и его транспортирования к потребителям. Источниками теплоснабжения (особенно для крупных городов) являются теплоэлектроцентрали (ТЭЦ), на которых вырабатывается электрическая энергия, а отработанный пар используется для нужд теплоснабжения. Способ одновременной выработки электрической энергии и тепла носит название комбинированного, а система централизованного теплоснабжения в этом случае называется теплофикацией. По виду теплоносителя системы центрального теплоснабжения разделяются на водяные и паровые. В нашей стране широкое распространение получили водяные двухтрубные системы теплоснабжения. На рис. 2.1.4.-1 показана принципиальная схема системы теплоснабжения. Согласно этой схеме, теплоноситель подготавливается на ТЭЦ (1) и затем по трубопроводу прямой магистрали с помощью насосной станции подается в системы отопления, вентиляции и горячего водоснабжения зданий. В нагревательных приборах, расположенных внутри зданий, теплоноситель отдает часть аккумулированного в нем тепла и отводится по обратной магистрали (4) к источнику тепла. Для обеспечения циркуляции теплоносителя необходимо в источнике (или на насосных подкачивающих станциях) создать такой напор, чтобы с учетом потерь давления в наиболее удаленных от источника тепла узлах он был бы в следующих пределах:
НВС £ НП £ НПР;
для обратной магистрали:
НЗД + 5 £ НО £ НДОП,
где НВС – давление, при котором происходит вскипание теплоносителя; НПР – допустимый по давлению предел прочности труб; НЗД – высота здания; НДОП – давление, назначаемое, исходя из прочностных характеристик отопительных приборов или теплообменных аппаратов.
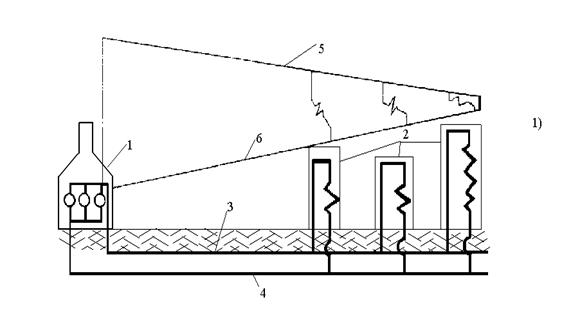
Рис. 2.1.4. Устройство двухтрубных тепловых сетей
1)принципиальная схема системы теплоснабжения: 1 – источник (ТЭЦ, районная котельная), 2 – система отопления и вентиляции здания, 3 – прямая магистраль, 4 – обратная магистраль, 5 – линия напора в прямой магистрали, 6 – то же в обратной.
2)схема системы водоснабжения города: 1 – котельная, 2 – магистральная кольцевая сеть, 3 – контрольно-распределительный пункт (КРП), 4 – распределительные тепловые сети,
5 – центральный тепловой пункт (ЦТП), 6- то же индивидуальные, 7 – электрокотельная.
3) схема подключения абонентов к тепловым сетям: 1 – система центрального отопления, 2 – калориферы вентиляции, 3 – система центрального горячего водоснабжения, 4 –технологические потребители тепла, 5 – бак горячей воды, 6 – элеватор или инжектор, 7 – насос центробежный, 8 – поверхностный водоподогреватель, 9 –терморегулятор, 10 – регулятор давления, 11 – обратный клапан, 12 – конденсатоотводчик, 13 – задвижки, 14 – регулятор уровня, 15 – холодный водопровод, 16 – сместительный водонагреватель, 17 – падающая магистраль, 18 – обратная, 19 – источник теплоснабжения.
На рис. 2.1.4.-2 представлена схема современной централизованной системы теплоснабжения города. Согласно этой схеме, тепло от нескольких источников (ТЭЦ, районных котельных и электробойлерных, работающих в пиковом режиме), подается в кольцевую сеть. От кольцевой сети тепло поступает в контрольно-распределительные пункты и далее через распределительную разветвленную сеть к центральным тепловым пунктам (ЦТП). На ЦТП производится подготовка теплоносителя и разделение его на отопительную нагрузку горячего водоснабжения. От ЦТП вода поступает через абонентские вводы в жилые и общественные здания.
На рис. 2.1.4.-3 представлены возможные схемы подключения абонентов к тепловой сети:
а,д,ж – непосредственное присоединение;
б – через элеваторный узел;
в – с помощью насосных установок;
г,е,и – через теплообменные аппараты.
9.3 Проектирование технологических процессов.
Объектом регулирования называется такой объект (агрегат, аппарат, установка, машина, помещение), в котором автоматический регулятор поддерживает заданное значение регулируемой величины или изменяет ее по заданному закону. В САР объект регулирования представляется как звено в цепи, свойство и характеристики которого имеют существенное значение для процесса регулирования. Объекты регулирования изучаются в автоматике с точки зрения их свойств на процессы поддержания заданных параметров при изменениях нагрузок. Важно иметь в виду, что интерес представляют не стационарные процессы и состояния равновесия, а именно переходные процессы из одного равновесного состояния в другое. Поэтому необходимо изучать и оценивать объекты регулирования в тот момент, когда регулируемый параметр изменяет свое значение, т.е. изучаются динамические свойства объектов регулирования. К ним относятся такие свойства, как емкость объекта, запаздывание, скорость разгона или чувствительность объекта к возмущениям, самовыравнивание и степень самовыравнивания, постоянная времени объекта, а также характер возмущающих воздействий.
При изменении регулируемого параметра в объекте регулирования проявляются такие свойства его, как аккумуляционная способность, т.е. способность накапливать вещество или энергию. Для характеристики этого свойства пользуются понятием коэффициент емкости объекта, под которым понимается величина, равная количеству вещества или энергии, необходимая для изменения регулируемого параметра на единицу измерения.
При регулировании уровня воды в баке коэффициент емкости есть количество воды, которое нужно подать в бак с тем, чтобы изменить уровень на 1 см или другую линейную величину, т.е.
,
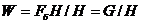где W – коэффициент емкости объекта, м3/см;
Fб – поверхность бака, м2;
H – высота уровня, м;
G – объем воды в баке, м3.
Коэффициент емкости объекта для краткости принято называть просто емкостью объекта регулирования. Это свойство объекта регулирования важно иметь в виду, так как оно оказывает непосредственное влияние на скорость изменения регулируемого параметра (3.3.1). Если объект регулирования обладает малой емкостью, то регулируемый параметр изменяется быстро, и наоборот. С точки зрения регулирования ясно, что при более быстром изменении регулируемого параметра удержать его в пределах труднее. Таким образом, объект, обладающий большим коэффициентом емкости, имеет преимущество перед объектом с малой емкостью, так как на объект с большой емкостью можно ставить более простой регулятор при прочих равных условиях.
Для помещения, в котором регулируется температура внутреннего воздуха, коэффициент емкости – это количество тепла, необходимое для изменения температуры в объекте на 1 °. Тепло расходуется в этом объекте на нагрев находящихся предметов и окружающих поверхностей. В некоторых случаях рекомендуется определять коэффициент емкости для помещения по следующей формуле:
,
где Wn – коэффициент емкости помещения при регулировании температуры;
См – удельная теплоемкость материалов предметов, находящихся в помещении;
Gм – масса материалов предметов, находящихся в помещении;
F – площадь ограждающих помещение поверхностей;
a¢ - количество тепла, воспринимаемое или отдаваемое единицей поверхности огражде-
ний при изменении температуры в объекте на 1 °.
Указанное выше выражение для определения коэффициента емкости помещения как объекта регулирования будет справедливо только при очень медленных изменениях температуры, когда все предметы, находящиеся в помещении, успеют прогреться. Сам коэффициент емкости будет изменяться в зависимости от скорости изменения температуры. Зависимость эта весьма сложная, связанная с нестационарными тепловыми процессами и аналитическое решение ее на сегодня еще не представляется возможным. В связи с этим первостепенное значение приобретают экспериментальные данные. Строго говоря, для получения коэффициента емкости помещения необходимы измерения непосредственно в этом помещении. А так как помещения очень часто могут быть однотипными, то для получения сравнительных данных по коэффициентам емкости не потребуется большого количества экспериментов. Помещения, как объекты регулирования, обладают еще способностью накапливать и влагу за счет гигроскопических свойств материалов, находящихся в помещении, и ограждающих частей здания. Известно, что процессы влагообмена взаимосвязаны с процессами теплообмена и протекают всегда совместно. Все это еще больше усложняет задачу определения коэффициента емкости помещения, как в случае регулирования температуры, так и при регулировании относительной влажности воздуха в помещении. Коэффициент емкости помещения при регулировании влажности также может быть определен только на основе опытных данных, тем более, что процессы влагообмена в настоящее время изучены еще очень мало.
Из практики, например, известно, что при регулировании относительной влажности в помещениях последняя изменяется значительно быстрее, чем температура. Это означает, что помещения обладают существенно меньшим коэффициентом емкости при регулировании влажности, чем при регулировании температуры. Отсюда следует, что поддерживать относительную влажность в помещениях более сложно, чем температуру.
Запаздывание или отставание во времени начала изменения регулируемого параметра от начала появления возмущения как свойство объектов регулирования – явление нежелательное, так как с увеличением запаздывания обычно ухудшается процесс регулирования, т.е. увеличиваются отклонения регулируемого параметра при возмущениях. Поэтому необходимо стремиться к снижению запаздывания. С этой точки зрения нужно иметь в виду, что объекты регулирования могут быть одноемкостными, двухъемкостными и многоемкостными.
В одноемкостных объектах регулируемая величина при возмущающих воздействиях изменяется сразу же после достижения регулирующей средой объекта. Пример такого одноемкостного объекта приведен на рис. 3.3.2.-а. На рис. 3.3.2.-б приведен пример двухъемкостного объекта, для которого вода подается вначале в промежуточную емкость (бак 1) и поступает в объект регулирования (бак 2) через гидравлическое сопротивление Rг. Таким образом, в двухъемкостном объекте регулирования имеются две последовательно включенные емкости: одна на стороне подачи (бак 1) и другая на стороне потребления (бак 2). Обе емкости разделены сопротивлением, от величины которого зависит как разность уровней в баках 1 и 2, так и количество воды, перетекающей из одного сосуда в другой.
Если приток жидкости в бак 1 внезапно увеличится, то уровень в нем начнет сразу же меняться. В начальный после возмущения период из-за наличия гидравлического сопротивления перетеканию жидкости из одного сосуда в другой уровень в баке 2 (регулируемая величина) будет изменяться незначительно. По мере увеличения уровня в баке 1 отклонение нарастает более интенсивно. Таким образом, в двухъемкостном объекте имеет место отставание регулируемого параметра от изменения величины притока, т.е. объект обладает запаздыванием. Если же возмущение произойдет за счет изменения расхода воды из бака 2, то уровень в нем (регулируемый параметр) изменится сразу же, без отставания или запаздывания, т.е. так же, как в одноемкостном объекте. Таким образом, следует иметь в виду, что в двухъемкостных объектах характер изменения регулируемого параметра может быть различен в зависимости от того, где и за счет чего возникает возмущение, нарушающее равновесие.
В нашем примере возмущающее воздействие происходит за счет изменения величины Qст при истечении из бака 2, а регулирующее воздействие – соответствующее изменение Q пр при притоке в сосуд 1. Это регулирующее воздействие в двухъемкостном объекте осуществляется с запаздыванием на стороне подачи (бак 1) и за счет преодоления гидравлического сопротивления Rr.. Величина этого запаздывания будет тем больше, чем больше коэффициент емкости на стороне подачи W1 (коэффициент емкости сосуда 1) и чем больше гидравлическое сопротивление между баком 1 и 2 (межъемкостное сопротивление).
На рис. 3.3.2-б показано, что при увеличении поверхности бака 1 его коэффициент емкости W¢1 будет больше, следовательно, запаздывание также будет больше.
Итак, двухъемкостные объекты регулирования, а также, очевидно, и многоемкостные обладают запаздыванием, которое характеризуется отставанием регулирующего воздействия на регулируемый параметр после изменения поступления вещества или энергии в емкость на стороне подачи. Этот вид запаздывания называют емкостным, или переходным. Оно, по сути дела, есть время, которое связано с замедлением изменения регулируемого параметра в двухъемкостных или многоемкостных объектах по сравнению с одноемкостными.
Примером двухъемкостного объекта регулирования может служить любой теплообменный аппарат. Если рассмотреть водо-водяной подогреватель, то в нем емкостью на стороне подачи является тепло, заключенное в массе теплоносителя, а емкостью на стороне потребления – тепло, заключенное в массе нагреваемой воды. Межъемкостным сопротивлением является термическое сопротивление трубок (стенок) теплообменника. Переходное запаздывание в теплообменных аппаратах зависит от термического сопротивления между емкостями и емкости на стороне подачи, т.е. от количества тепла, содержащегося в теплоносителе в этой емкости. Вследствие емкостного запаздывания после пуска горячей воды (теплоносителя), например, в водяной подогреватель, температура подогреваемой воды изменяется не сразу: сначала нагревается металл теплообменника, и между теплоносителем и подогреваемой водой возникает разность температур, соответствующая тепловой нагрузке аппарата. Только через некоторое время температура подогреваемой воды начнет повышаться. Следовательно, регулирующее воздействие на двухъемкостный объект передается не сразу, а с отставанием на величину переходного запаздывания.
Преимущество имеют те объекты регулирования, которые обладают минимумом емкостного запаздывания. Поэтому в теплообменных аппаратах необходимо предусматривать минимально возможную толщину стенок и изготовлять их из малотеплоемких металлов, имеющих значительные коэффициенты теплопроводности. Кроме того, необходимо, чтобы количество греющей воды в емкости на стороне подачи было также минимальным.
Запаздывание может происходить не только в объектах многоемкостных или передаточное запаздывание наблюдается и в одноемкостных объектах. Этот вид запаздывания связан со временем, необходимым для доставки (транспорта) вещества или энергии к объекту регулирования. Причина чистого запаздывания заключается в том, что регулирующему сигналу (в виде измененного значения Qпр или Qст) требуется известное время для перехода от регулирующего органа к объекту.
В вентиляционных установках этот вид запаздывания весьма существенен и зависит от кратности воздухообмена, способа раздачи приточного воздуха и от относительных размеров помещения.
В качестве примера рассмотрим опорожнение призматического резервуара, имеющего постоянную площадь поперечного сечения W. Предположим, что в дне резервуара устроено отверстие площадью w, начальный напор над центром тяжести которого равен Н1, а конечный – Н2 (рис. 3.3.3). Предположим, что во время опорожнения резервуара жидкость в него поступать не будет.
Расчет опорожнения резервуара заключается в определении времени этого процесса. Когда отверстие открыто, то за время dt из резервуара вытекает объем жидкости dW:
,
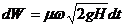где Н – напор над центром тяжести отверстия в момент времени t.
Одновременно уровень в резервуаре опустится на величину
.
Следовательно,
,
знак минус взят здесь потому, что напор уменьшается. Как видно,
.
Проинтегрируем это уравнение в пределах от Н1 до Н2:
;
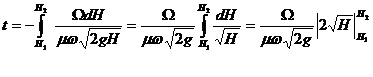окончательно будем иметь:
.
Полагая в формуле Н2 = 0, получим формулу для времени полного опорожнения резервуара:
,
или
,
где W – объем жидкости в резервуаре;
Q – расход жидкости при начальном напоре Н1.
Пусть m = 1.1; 
; d = 0.1;
w = 0.00785; д = 9.81 м2/ сек;
W - площадь резервуара = 25 м2;
Н1 = 10 м; W – объем резервуара = 250 м3;
Q = 1.1×0.00785× 
= 0.12 м3/сек.
tопорожнения - 2×250 / 0.12 = 4166.7 сек или t = 1.16 час.
Для различных объектов регулирования характерны разные скорости изменения регулируемого параметра, которые во многом определяют процесс регулирования. Действительно, при быстрых изменениях регулируемого параметра следует также быстро осуществлять регулирующее воздействие, так как в противном случае регулируемый параметр успеет отклониться на существенную величину. Если же в объекте регулирования скорость изменения регулируемого параметра невелика, то за время передачи сигнала регулируемый параметр отклонится сравнительно меньше.
Таким образом, можно сказать, что если в объекте регулирования регулируемый параметр будет меняться медленно, то такой объект обладает лучшими свойствами, чем объект, в котором изменение регулируемого параметра происходит значительно быстрее.
На быстроту изменения регулируемого параметра оказывает существенное влияние коэффициент емкости объекта регулирования, как это видно из рис. 3.3.1. Для более точной сравнительной характеристики объектов регулирования вводят понятие «чувствительность объекта к возмущению» или «скорость разгона», имея в виду именно сравнительную оценку объектов по скорости изменения регулируемого параметра. Чувствительность объекта к возмущению определяется на основе следующих условий.
Представим себе такой объект регулирования, как бак с водой, в котором регулируемым параметром Р является уровень Н. Вода в сосуд подается и откачивается с помощью насоса. Схематически это представлено на рис. 3.3.4. Регулируемый параметр – уровень будет неизменным до тех пор, пока Qпр = Qст. При нарушении этого равновесия он будет непрерывно изменяться. В данном примере Qпр и Qст зависят только от числа оборотов насоса, потому нарушение равенства Qпр = Qст приводит к беспрерывному изменению уровня до тех пор, пока вода не будет переливаться или полностью не опорожнится сосуд. Такие объекты регулирования называются объектами регулирования без самовыравнивания.
Нетрудно предположить, что скорость изменения регулируемого параметра для объекта прямо пропорциональна разности между Qпр - Qст и обратно пропорциональна коэффициенту емкости объекта. Для бесконечно малого промежутка времени dt можно считать, что эта зависимость линейная, т.е.
,
где dP – бесконечно малое изменение регулируемого параметра за бесконечно малый отрезок времени dt;
Qпр – текущее значение притока;
Qст – текущее значение стока;
W - коэффициент емкости объекта;
DQ – разность между притоком и стоком, определяющая скорость изменения регулируемого параметра и называемая возмущающим воздействием или возмущением.
Последняя формула часто записывается в виде безразмерного выражения, так как это оказывается более удобным для математического решения уравнений. Для этого отнесем все текущие величины к их номинальному заданному значению. Получим соответственно:
nпр = Qпр / Qном - относительный приток, nст = Qст / Qном – относительный сток. Принимаем также, что абсолютные значения номинального притока и стока равны. Обозначим текущее значение регулируемого параметра через Р. Тогда безразмерное значение величины регулируемого параметра s получим, разделив текущее значение регулируемого параметра на номинальное заданное его значение, т.е. s = Р / Рном. Тогда бесконечно малое относительное приращение параметра
ds = dP / Pном.
Теперь заменим в формуле 3.3.1 абсолютные величины на их относительные значения. В этом случае после соответствующих подстановок формула (3.3.1) будет иметь следующий вид:
ds / dt = (1 / W) (Q ном / Рном) (nпр - nст) = eDn, (3.3.2)
где e - коэффициент пропорциональности, называемый чувствительностью объекта к возмущению, или скоростью разгона, 1/с.
e = (1 / W) / (Qном / Р ном).
Величина, обратная чувствительности объекта к возмущению, т.е.
Ta = 1 /e = WP ном / Qном ,
называется временем разгона Та и имеет размерность времени. Произведение WРном представляет собой количество вещества или энергии, накопленное в объекте при достижении номинального, т.е. заданного, значения регулируемого параметра от его нулевого значения. Для нашего примера – это количество воды в сосуде, которое содержится при заданном уровне. Если WРном разделить на номинальное значение либо стока, либо притока вещества или энергии, то частное от деления Та есть время, необходимое для достижения величины регулируемого параметра Р от 0 до Рном при условии, что процесс осуществляется с постоянной скоростью, когда Qст = 0, а Qпр = Qном.
Таким образом, Та – время наполнения или опорожнения бака при постоянной скорости, когда возмущение максимально заданное.
Теперь нетрудно представить физически и величину e. Чувствительность объекта к возмущению представляет собой скорость изменения регулируемого параметра в относительных величинах при максимальных возмущающих воздействиях, т.е. при Dn = 1, что соответствует Qст = 0, а Qпр = Q ном. В нашем примере скорость изменения параметра представлена в отношении к максимальному заданному значению Qпр при Qст = 0. Тогда в общем случае относительная скорость изменения регулируемого параметра представлена в долях от полной емкости объекта регулирования (при изменении Р от 0 до Рном ) при достижении заданного значения регулируемого параметра.
Итак, если Та показывает время наполнения бака, то e - какую часть бака можно заполнить за единицу времени. Если Та выражается обычно в секундах, то e - часть бака, которая заполнится за 1 с в результате максимального возмущающего воздействия. Или e есть скорость изменения регулируемого параметра в долях от единицы, когда за единицу принято изменение от Р = 0 до Р = Рном.
Если заменить e на Та, то выражение 3.3.2 можно представить в следующем виде:
Та (ds / dt) = Dn. (3.3.3)
Из 3.3.2 и 3.3.3 при Dn = 1 видно, что e максимально и меняется пропорционально Dn. Таким образом, скорость разгона объекта регулирования пропорциональна величине возмущающего воздействия на объект. При малых возмущениях имеют место небольшие скорости изменения регулируемого параметра. Для объектов систем ОВК как раз характерны незначительные возмущения, что свидетельствует об их положительных, с точки зрения регулирования, свойствах.
Свойство объекта регулирования – самостоятельно (без регулятора) выравнивать значения Q ст и Q пр, т.е. с течением времени приходить к новому равновесному состоянию после однократного скачкообразного (Dt = 0) возмущения, называется самовыравниванием объекта регулирования. При достижении нового равновесного состояния в объекте устанавливается равенство между притоком и стоком вещества. Регулируемый параметр стабилизируется на новом значении. Объект, обладающий самовыравниванием, с течением времени уменьшает полученное возмущение, доводя это возмущающее воздействие до нуля. Если возмущение произошло за счет изменения притока, а новое равновесное состояние достигается объектом за счет уменьшения или увеличения стока вещества или энергии, то такой объект обладает самовыравниванием на стороне стока. В таком объекте величина стока зависит от значения регулируемого параметра. Если в объекте регулирования сток изменяется однократно и скачкообразно, а равновесие достигается за счет увеличения и уменьшения притока, то такой объект обладает самовыравниванием на стороне притока. На рис. 3.3.5 изображен объект, не обладающий самовыравниванием, так как в нем величина притока и стока не зависит от регулируемого параметра уровня. В таком объекте малейшие нарушения равенства между притоком и стоком приводят к беспрерывному изменению регулируемого параметра уровня. Естественно, что в объектах, не обладающих самовыравниванием, труднее поддерживать постоянное значение регулируемого параметра, т.е. осуществлять автоматическое регулирование.
Для установок и устройств систем ОВК характерным будет наличие самовыравнивания в объектах регулирования. В целом ряде случаев встречаются объекты регулирования, которые обладают самовыравниванием одновременно на притоке и стоке. Рассмотрим объекты, обладающие самовыравниванием. На рис. 3.3.5 изображен бак, в который подается вода из водопровода. Сток осуществляется под действием гидростатического давления, т.н. в зависимости от величины уровня. В таком объекте Q ст = f (H), а в общем случае Q ст = f (P).
На рис. 3.3.5 показан бак, в котором приток определяется уровнем воды в нем. Сток осуществляется при помощи насоса, и величина его не зависит от уровня. Такой объект обладает самовыравниванием на стороне притока.
Отапливаемое помещение (рис. 3.3.5), в котором поддерживается постоянная температура за счет отдачи тепла нагревательным прибором, в качестве объекта регулирования, обладает самовыравниванием как на стороне стока, так и на стороне притока. Действительно, если увеличится отдача тепла нагревательным прибором, т.е. увеличится Qпр, то за счет увеличения температуры внутри этого помещения возрастут и потери тепла, т.е. Qст. В этом случае Qст = f (P).
При уменьшении потерь тепла, которые происходят за счет увеличения наружной температуры, возрастает температура внутри помещения. А если повышается температура, то непременно изменяется и отдача тепла нагревательным прибором, т.е. Qпр = f (P). Таким образом, при изменениях регулируемого параметра – температура внутри отапливаемого помещения – изменяются одновременно потери тепла и теплоотдача нагревательным прибором, т.е. в этом объекте приток и сток зависят от величины регулируемого параметра. Такие –объекты обладают самовыравниванием на стороне стока и притока, а следовательно, автоматическое регулирование в них осуществляется проще.
Наличие или отсутствие самовыравнивания в объектах регулирования характеризует их только с качественной стороны. Необходимо иметь и количественную оценку объектов регулирования с точки зрения самовыравнивания. Действительно, одни объекты регулирования могут обладать большой степенью самовыравнивания, а другие весьма незначительной. Для суждения об этом и служит понятие о степени самовыравнивания.
Представим себе объект, обладающий самовыравниванием на стороне стока (рис. 3.3.5). В нем, в отличие от объекта без самовыравнивание, уравнение 3.3.1 будет иметь вид:
W (dP / dt) + aP = Qпр, (3.3.4)
где a - коэффициент пропорциональности, показывающий зависимость Qст = aP.
Уравнение (3.3.4) после умножения и деления левой части уравнения на номинальное значение параметра, а правой – на номинальное значение Qпр = Qном, в безразмерной форме примет следующий вид:
или
.
Обозначим
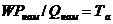; aРном / Qном = 
r;
Qпр /Qном = n.
Тогда
Та ds / dt + rs = n. (3.3.5)
Уравнение (3.3.5) является уравнением объекта с самовыравниванием, записанное в безразмерном виде. Коэффициент пропорциональности r называют степенью самовыравнивания. Величину степени самовыравнивания r объекта регулирования только в первом приближении можно принять постоянной, так как она в процессе самовыравнивания объекта меняется. Степень самовыравнивания r характеризует объект с точки зрения способности его к самовыравниванию и показывает величину ослабления относительного возмущения на единицу отклонения регулируемого параметра в относительных величинах. Чем больше r, тем большая величина возмущения «гасится» за счет свойств самого объекта регулирования. В таком объекте легче поддерживать заданное значение регулируемого параметра.
Величину r приближенно можно определить как отношение относительного возмущения к величине отклонения регулируемого параметра в относительных единицах.
Если все члены выражения (3.3.5) поделить на r, то его можно преобразовать к следующему виду:
(Та / r) (ds / dt) +s = (1 / r) n. (3.3.6)
Обозначив 1 / r = k и Та / r = Т, подставив их в уравнение (3.3.6); получим
Т (d s / dt) +s = k n, (3.3.7)
где Т – постоянная времени объекта, с;
k – коэффициент усиления, характеризующий эффективность регулирующего воздействия, величина, обратная степени самовыравнивания.
Выражения (3.3.5) - (3.3.7) являются уравнениями динамики процесса изменения регулируемого параметра после однократного скачкообразного возмущения в объектах с самовыравниванием. Решение уравнения (3.3.7) дает экспоненциальную зависимость s от t:
s = k n (1-е-t/T). (3.3.8)
Выражение (3.3.8) в осях s - Т представляет собой кривую изменения во времени относительной величины регулируемого параметра с момента начала изменения s после приложения к регулируемому объекту некоторого скачкообразного относительного возмущения. Эта кривая является динамической характеристикой объекта и называется кривой самовыравнивания. Она представляет собой выраженную графически зависимость, характеризующую изменение регулируемого параметра во времени после внесения однократного скачкообразного возмущения, после которого процесс изменения параметра считается протекающим самостоятельно, без влияния внешних воздействий.
В выражении (3.3.8) видно, что отношение Та / r = Т является величиной постоянной. Это отношение называют постоянной времени экспоненты. На кривой самовыравнивания она численно равна длине отрезка асимптоты экспоненты, заключенного между ординатой, проходящей через начальную точку этой кривой, и точкой пересечения асимптоты с касательной к экспоненте, проведенной в той же точке.
Величина Т называется постоянной времени объекта и показывает время, которое потребовалось бы для достижения нового предельного значения параметра при сохранении начальной скорости его изменения.
Время полного самовыравнивания с достаточной для практических целей точностью можно определить из приближенного выражения.
tп.с = 3Т.
Через промежуток времени t п.с, определенный из последнего выражения, s достигнет значения, отличающегося от sк на величину, равную примерно 5 % от разности sк - sн.
Величина степени самовыравнивания объектов регулирования во многом определяет их динамические характеристики. Объекты имеют устойчивую динамическую характеристику, если r>0, нейтральную, если r=0 и неустойчивую, если r<0. Вид этих характеристик изображен на рис. 3.3.7.
Практика показывает, что при значениях степени самовыравнивания, близких к единице, и чувствительности к возмущениям, не превышающей 0,0005 1/с, объект можно считать обладающим хорошими в отношении регулирования динамическими свойствами, которые позволяют применить простейшие типы регуляторов.
Отметим, что динамические характеристики объектов регулирования теоретически, расчетным путем получить пока в целом ряде случаев не удается. Поэтому кривую самовыравнивания объектов регулирования получают на основе экспериментальных данных. Для этого объекту регулирования во время установившегося равновесного состояния сообщается возмущающее воздействие, величина которого измеряется. Затем снимают с помощью самопишущих приборов картину изменения регулируемого параметра во времени. Изменение регулируемого параметра целесообразно проследить до тех пор, пока он не станет постоянным.
Кроме того, следует следить за тем, чтобы во время опыта не возникли другие неучтенные возмущения.
Полученная таким образом кривая самовыравнивания объекта регулирования дает основания для установления величин r, e и Т.
Степень самовыравнивания можно получить, разделив начальное возмущающее воздействие Dn0, которое было измерено в относительных величинах, на полученное из эксперимента отклонение параметра, также выраженное в относительных величинах, т.е.
r = Dn0 / (sк -sн). (3.3.9)
Постоянная времени объекта может быть определена как частное от деления приращения регулируемого параметра в относительных величинах на тангенс угла a наклона касательной в начальной точке кривой экспоненты. Возможно установление постоянной времени после графического построения
Т = (sк - sн) / tg a. (3.3.10)
Для получения чувствительности к возмущению нужно иметь в виду, что
Т = Та / r и Та = 1 / e.
Тогда имеем Тr = Та = 1 / e или e = 1 / (Тr).
Последние Т и r нами уже были определены. Отсюда
. (3.3.11)
Для полной оценки объектов регулирования представляется весьма важным учесть характер изменения нагрузок. Действительно, если исходить из теоретических рассуждений, то характер изменения нагрузок может быть принят только скачкообразный. Иначе математическое решение уравнений окажется невыполнимым. С точки зрения инженерного подхода принятие характера изменения нагрузок скачкообразным правильно, так как в этом случае объект ставится в самые невыгодные условия. Однако на практике не встречается скачкообразный характер изменения нагрузок, если говорить о системах отопления и вентиляции. можно и нужно говорить в абсолютном большинстве случаев о плавном характере изменения нагрузок, т.е. о таком изменении нагрузок в объекте, когда они происходят за довольно-таки большой промежуток времени. а это существенно меняет процесс регулирования и, как правило, в лучшую сторону. Поэтому, сравнивая два объекта регулирования, всегда нужно иметь в виду, что тот объект, в котором нагрузки изменяются более плавно, имеет лучшие динамические свойства и для него потребуется более простой автоматический регулятор при всех остальных одинаковых характеристиках.
Не менее важно для оценки объектов регулирования знание частоты изменения нагрузок. Действительно, при частых изменениях нагрузок регулятор срабатывает более часто и, следовательно, быстрее изнашивается. Помимо этого может случиться и так, что вторичное изменение нагрузки наступит ранее, чем объект придет к равновесию после полученного первичного возмущения. В таком случае отклонения регулируемого параметра, как правило, выходят за пределы предполагаемых. Объект, в котором более часто изменяются нагрузки при прочих равных условиях, имеет худшие динамические характеристики. В практике это обстоятельство, очевидно, следует учитывать, ориентируясь, главным образом, на данные, полученные из опыта.
При рассмотрении характера изменения нагрузок в объекте регулирования не менее существенно знать о возможных предельных колебаниях возмущающих воздействий. Самым невыгодным случаем здесь являются колебания нагрузок от 0 до максимума.
В качестве примера рассмотрим случай выравнивания уровней в сообщающихся сосудах.
