Остаточные напряжения сжатия, возникающие при сварке, могут вызвать потерю местной устойчивости тонких пластин. Чтобы пластина не потеряла устойчивости, должно быть выполнено следующее условие:
sсв + sвн £ sкр, (4.8)
где sсв – напряжения сжатия, вызванные сваркой;
sвн – напряжения сжатия от внешних нагрузок;
sкр – критические напряжения, зависящие от соотношения размеров пластины и характера закрепления ее кромок.
Критические напряжения выражаются формулой
(4.9)
где k – коэффициент, учитывающий соотношение размеров пластины и характер закрепления ее кромок;
n – коэффициент Пуассона, принятый равным 0,3;
d и b – соответственно толщина и ширина пластины.
Значения коэффициентов k и А для различных условий закрепления приведены в табл. 4.1 и 4.2.
Таблица 4.1 –Коэффициенты k и А для определения σ кр пластины, сжатой в одном (продольном) направлении
| Граничные условия | Коэффициенты | Значения k и А при отношении сторон пластины | |||||||||
| 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 3.0 | ∞ | ||
| Все края шарнирно оперты (рис. 4.6а) | k A | 5,14 4,63 | 4,20 3,78 | 4,00 3,60 | 4,13 3,72 | 4,47 4,02 | 4,20 3,78 | 4,05 3,64 | 4,00 3,60 | − − | 4,00 3,60 |
| Все края защемлены | k A | − − | − − | 9,40 8,46 | 9,30 8,37 | 8,80 7,92 | 8,50 7,65 | 8,50 7,65 | 8,20 7,38 | 7,80 7,02 | 7,0 6,30 |
| Края х = 0, х =а шарнирно оперты; края у = 0, у =b защемлены | k A | 7,05 6,35 | 7,29 6,56 | 7,69 6,92 | 7,15 6,44 | 7,04 6,34 | 7,20 6,48 | 7,05 6,35 | 7,0 6,30 | 7,15 6,44 | 7,0 6,30 |
| Края х = 0, х = а защемлены, края у = 0, у =b шарнирно оперты | k A | 13,38 12,04 | 8,73 7,86 | 6,74 6,07 | 5,14 5,26 | 5,45 4,90 | 5,34 4,81 | 5,18 4,66 | 4,85 4,36 | 4,41 3,96 | 4,0 3,60 |
| Края х = 0, х = а шарнирно оперты; край у = b защемлен; край у = 0 свободен (рис. 4.6в) | k A | − − | 2,70 2,43 | 1,70 1,53 | 1,47 1,32 | 1,36 1,?2 | 1,33 1,20 | 1,34 1,21 | 1,38 1,24 | 1,36 1,22 | 1,33 1,20 |
| Края х = 0, х = а и y=b шарнирно оперты, край у = 0 свободен (рис. 4.6б) | k A | 3,65 3,10 | 2,15 1,93 | 1,44 1,30 | 1,14 1,03 | 0,95 0,85 | 0,84 0,76 | 0,76 0,68 | 0,70 0,63 | 0,56 0,50 | 0,46 0,41 |
Таблица 4.2 –Коэффициенты k и А для определения sкр пластины, сжатой в двух направлениях (рис. 4.6г )
| Отношение сторон пластины а/ b | Коэффициенты | Значения k и A при | |||||
| 0,2 | 0,4 | 0,6 | 0,8 | 1.0 | 2,0 | ||
| 1 | k | 3,36 | 2,85 | 2,50 | 2,22 | 2,0 | 1,33 |
| А | 3,03 | 2,56 | 2,25 | 2,00 | 1,80 | 1,20 | |
| 2 | k | 3,36 | 2,40 | 1,84 | 1,49 | 1,25 | 0,69 |
| А | 3,03 | 2,16 | 1,66 | 1,34 | 1,12 | 0,62 | |
| 3 | k | 3,24 | 2,42 | 1,74 | 1,36 | 1.11 | 0,58 |
| А | 2,90 | 2,17 | 1,56 | 1,22 | 1,00 | 0,52 | |
| ∞ | k | 3,20 | 2,40 | 1,67 | 1,25 | 1,00 | 0,50 |
| А | 2,88 | 2,16 | 1,50 | 1,12 | 0,90 | 0,45 | |
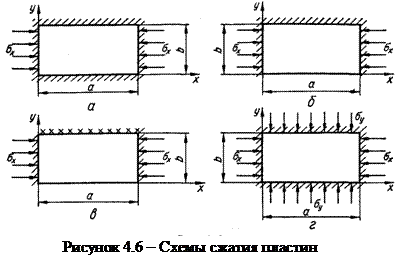
Схемы сжатия пластин приведены на рис. 4.6. Если условие по формуле (4.8) не удовлетворяется и sсв + sвн > sкр, то пластина потеряет устойчивость и появится выпучина, стрелка прогиба которой
, (4.10)
где a = l – длина пластины.
При сварке полотнищ в результате образования напряжений сжатия s2 = sсв (рис. 4.7 а) возможно проявление общей потери устойчивости (рис. 4.7б).
Критические напряжения в этом случае
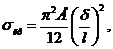(4.11)
где d и l – соответственно толщина и длина полотнища.
Стрелка прогиба полотнища в случае общей потери устойчивости может быть определена по формуле:
(4.12)
Формула (4.12) справедлива при 
.
Пример.
Две пластины из стали Ст3 размером 16×400×1000 мм (рис. 315а) свариваются встык двусторонним швом автоматической сваркой под флюсом на таком режиме:
I = 700 A; U == 30 В; v = 43 м/ч, h = 0,80. Определить: 1) величину угловых деформаций и стрелку поперечного прогиба пластины после выполнения швов 1 и 2 (рис. 4.8б, в);
2) произойдет ли общая потеря устойчивости полотнища после сварки;
3) величину предельной внешней сжимающей нагрузки, действующей вдоль продольной оси полотнища, исходя из условия, чтобы стрелка продольного прогиба полотнища была не более 0,8 см.
Решение.
1. Остаточные угловые деформации пластины после выполнения двустороннего шва будут определяться по формуле (4.1)
b = b1 + b2.
Из условия задачи следует, что выбранный режим сварки одинаковый для обоих проходов и обеспечивает глубину проплавления
h1 = h2 = 0,6d = 0,6 × 16 == 9,6 мм.
Угловая деформация b1 от шва 1 зависит от расчетной толщины dр = h 1 которая вызывает сопротивление угловым деформациям. Погонная энергия сварки
Рисунок 4.8 - Пластина, свариваемая стыковым швом
 |
Удельная погонная энергия (см. рис. 4.2)
кал/см.
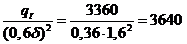кал/см3.
По графику рис. 4.2 определяем, что при v = 1,2 см/с и 
кал/см3 остаточная угловая деформация b1 = + 0,02 рад. При выполнении второго прохода (рис. 4.8 а) расчетное значение dр = d, а удельная погонная энергия
кал/см3.
Угловая деформация (обратного знака)
b2 = -0,017 рад
и суммарная угловая деформация
b = + 0,003 рад.
Стрелку поперечного прогиба f n определим по формуле (4.2)
см.
2. Для ответа на вопрос, произойдет ли общая потеря устойчивости пластины после сварки, необходимо определить остаточные напряжения сжатия s2 = sсв и сравнить их с критическими напряжениями по формуле (4.11).
По формуле (4.5)
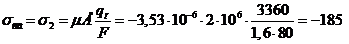кгс/см2.
Критические напряжения, приводящие к общей потере устойчивости пластины, найдем по формуле (4.11)
кгс/см2.
Расчеты показывают, что sсв < sкр, поэтому общая потеря устойчивости пластины после сварки не произойдет.
3. При приложении внешней осевой сжимающей нагрузки Р вн (рис. 4.8 а)в пластине возникнут напряжения сжатия величиной
Из формулы (4.10) определим величину 
при условии, что f = 0,8 см:
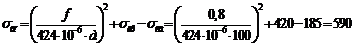кгс/см2.
Тогда
Р вн= s вн F = 590∙1,6∙80 = 75500 кгс =7,4∙105 Н.
Контрольные вопросы
1. Назовите причины образования угловой деформации при сварке.
2. Какова зависимость угловой деформация от относительной глубины провара и скорости сварки?
3. Как определить возможность потери устойчивости листового элемента от остаточных напряжений?
4. От чего зависит жесткость закрепления кромок листового элемента и как она учитывается при определении критического значения напряжения.
Лекция 5.
Расчет вторичных деформаций сварных элементов
План
5.1 Влияние внешних нагрузок на возникновение вторичных деформаций
5.2 Возникновение вторичных деформаций при механической обработке сварных конструкций
5.3 Классификация сварочных деформаций и напряжений
Под вторичными деформациями сварных конструкций подразумевают остаточную деформацию, возникающую в результате перераспределения внутренних остаточных напряжений. Это перераспределение может произойти при первом нагружении сварной конструкции, при механической, термической и газопламенной обработке сварных изделий.
