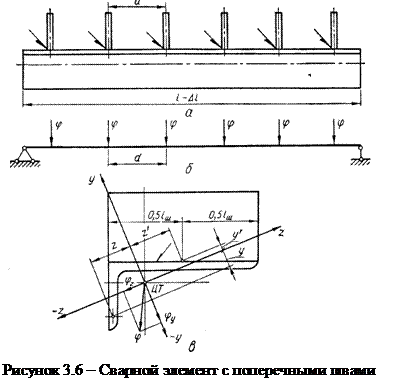
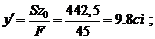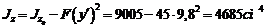При выполнении нескольких поперечных швов в элементе он будет испытывать деформации изгиба и укорочения. Так, например, приварка ребер к уголку (рис. 3.6 а) вызовет укорочение всего элемента и введет его в косой изгиб. Углы поворота элемента в обеих главных плоскостях (рис. 3.6б, в) и его абсолютное укорочение в продольном направлении по линии ЦТ от выполнения одного поперечного шва можно найти по зависимостям:
 |
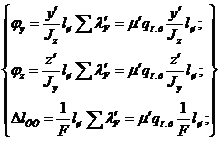(3.22)
где у', z' – координаты центра шва, см;
Jy, Jz – моменты инерции поперечного сечения элемента (уголка) относительно своих главных осей, см4;
l ш – длина шва, см;
qп.у – погонная энергия, приходящаяся на полку уголка, при приварке к нему ребра, кал/см;
F – площадь поперечного сечения элемента (уголка), см2;
Коэффициент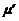 
рассчитывается по зависимости:
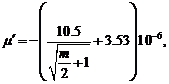(3.23)
где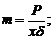 
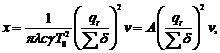
δ – толщина детали, которая при остывании получает поперечную деформацию, см;
v – скорость сварки в см/сек;
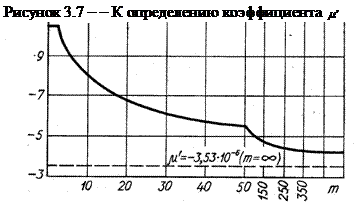
Значения вспомогательного коэффициента А для некоторых материалов даны в табл. 2.1. Последовательность вычислений деформации следующая: сначала вычисляют коэффициент х, затем – коэффициент т, потом по графику на рис. 3.7 определяют μ' и далее по формулам (3.22).
Стрелка прогиба элемента от выполнения п поперечных швов посредине пролета, считая пролет l = nd (рис. 3.6 а), и общая деформация элемента в продольном направлении составляют:
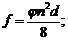(3.24)
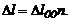
Иногда погонную энергию qп (кал/см) можно определять приближенно по катету углового шва исходя из соотношений:
при автоматической и полуавтоматической сварке
qп = 7250 К 2 (3.25)
при ручной сварке
qп = 9500 К 2 (3.26)
где К – катет шва, см.
Пример
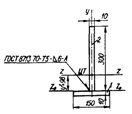
Определить общие деформации сварного тавра после выполнения автоматической сваркой одностороннего углового шва с катетом 6 мм. Длина шва равна длине тавра и составляет 10000 мм. Размеры поперечного сечения тавра указаны в табл. 3.2. Материал – углеродистая сталь Ст3.
Таблица 3.2 –Геометрические характеристики поперечного сечения тавра
| Эскиз | Номер детали | Площадь поперечного сечения детали F, см2 | Расстояние от центра тяжести детали до шва у', см | Статический момент относительно оси z 0 z 0 Sz 0 = Fy '. см | Момент инерции относительно оси z0z0 Jz0 |
|
| 1 2 | 15 30 | -0,5 -15 | -7,5 450 | 5 9000 |
| 1 и 2 | 45 | - | 442,5 | 9005 | |
|
| |||||
Решение.
1. По заданному катету шва находим qп по формуле (3.25)
qп = 7250 × 0,62 = 2610 кал/см.
2. Геометрические характеристики поперечного сечения тавра, необходимые для расчета, приведены в табл. 3.2.
3. Отношение погонной энергии к площади поперечного сечения тавра составляет
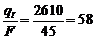кал/см3 <150 кал/см3
что, согласно таблице 2.1, позволяет применить расчетные формулы, приведенные выше.
Кривизну С и относительную продольную деформацию тавра по линии ЦТ D ЦТ определяем по формулам (3.4) и (3.8):
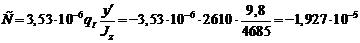1/см;
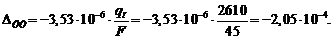
4. Абсолютное укорочение тавра определим по формуле (3.7)
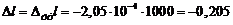см ≈ 2 мм.
5. Стрелку прогиба сварного тавра найдем по формуле (3.8)
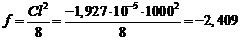см ≈ 24,1 мм
При этом тавр получит вогнутость со стороны полки (рис. 3.8).
Примеры для других вариантов сварных элементов и способов их сварки приводится в [1].
Контрольные вопросы
1. Что представляет собой деформация продольного укорочения и каковы причины ее образования? Дайте определение продольной усадочной силы.
2. Зависит ли величина продольной усадочной силы от режима сварки и размеров сварного соединения?
3. Что представляет собой деформация изгиба и каковы причины ее образования?
4. Какова методика определения деформации изгиба сварного соединения с несколькими швами?
5. В каких случаях образуется деформация изгиба сварного соединения в двух плоскостях?
6. Почему поперечные швы вызывают образование общих деформаций конструкций?
Лекция 4.
Расчет местных деформаций и остаточных напряжений
План
4.1 Классификация местных деформаций
4.2 Продольные остаточные напряжения и построение эпюр.Реактивные напряжения
4.3 Потеря местной устойчивости тонких пластин
