Задача Коши для дифференциального уравнения n -го порядка
 , (7.21)
, (7.21)
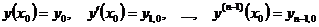 (7.22)
(7.22)
легко сводится к задаче Коши для системы дифференциальных уравнений с помощью замены переменных
 (7.23)
(7.23)
Учитывая (7.23) из уравнения (7.21) получим систему дифференциальных уравнений
 (7.24)
(7.24)
Начальные условия (7.22) для функций zl переписываются в виде
 . (7.25)
. (7.25)
Запишем для полученной системы метод Рунге-Кутта
 . (7.26)
. (7.26)
Для вычисления коэффициентов Kl ,1, Kl ,2, Kl ,3 и Kl ,4 имеем следующие формулы:


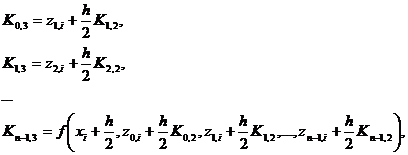

Пример 7.5. Решить задачу Коши для дифференциального уравнения третьего порядка
 ,
,

Решение в Excel. Точное решение данной задачи известно  . Преобразуем эту задачу с помощью замены
. Преобразуем эту задачу с помощью замены  к задаче для системы уравнений:
к задаче для системы уравнений:
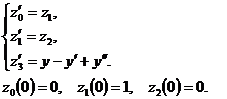
Точным решением системы теперь будут функции
 .
.
Выберем шаг h = 0,1. В программе Excel мы используем функции и алгоритм решения, созданные для решения примера 7.4.
Откроем файл примера 7.4 и внесем необходимые изменения. Результаты расчетов представлены в таблице 7.10.
1) Заменить функции f_1(), f_2() и f_3() на следующие:
Function f_1(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)
f_1 = 2 * x * y_1 / y_2
End Function
Function f_2(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)
f_2 = 8 * y_3 / (3 * y_2)
End Function
Function f_3(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)
f_3 = 3 * y_3 / y_1
End Function
Функции для вычисления коэффициентов Kl , I не изменяем.
2) Изменим начальные условия в ячейках B 3, C 3, D 3 на 0, 1, 0.
В столбце значений переменной xi вводим числа 0; 0,1; 0,2; …; 1.
В ячейках E 3, F 3, G 3 вводим соответственно формулы =SIN(A3), =COS(A3) и =-SIN(A3).
Таблица 7.10
| A | B | C | D | E | F | G | |
| 1 | h= | 0,1 |
|
| Точные решения | ||
| 2 | xi | y1i | y2i | y3i | y1=sinx | y2=cosx | y3=-sinx |
| 3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0,1 | 0,099833 | 0,995004 | -0,09983 | 0,09983 | 0,995 | -0,099833 |
| 5 | 0,2 | 0,198669 | 0,980067 | -0,19867 | 0,19867 | 0,98007 | -0,198669 |
| 6 | 0,3 | 0,29552 | 0,955337 | -0,29552 | 0,29552 | 0,95534 | -0,29552 |
| 7 | 0,4 | 0,389418 | 0,921061 | -0,38942 | 0,38942 | 0,92106 | -0,389418 |
| 8 | 0,5 | 0,479425 | 0,877583 | -0,47943 | 0,47943 | 0,87758 | -0,479426 |
| 9 | 0,6 | 0,564642 | 0,825336 | -0,56464 | 0,56464 | 0,82534 | -0,564642 |
| 10 | 0,7 | 0,644217 | 0,764843 | -0,64422 | 0,64422 | 0,76484 | -0,644218 |
| 11 | 0,8 | 0,717356 | 0,696707 | -0,71736 | 0,71736 | 0,69671 | -0,717356 |
| 12 | 0,9 | 0,783326 | 0,621611 | -0,78333 | 0,78333 | 0,62161 | -0,783327 |
| 13 | 1 | 0,84147 | 0,540303 | -0,84147 | 0,84147 | 0,5403 | -0,841471 |
Сравнивая столбцы B и E, видим, что метод Рунге-Кутта дает хорошие приближения к значениям точного решения y1=sinx.
Краевые задачи для обыкновенных дифференциальных уравнений
Примерами краевых задач для обыкновенных дифференциальных уравнений являются следующие задачи:
1) Найти функцию u (x), которая удовлетворяет на отрезке [ a, b ] уравнению
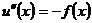 , (7.27)
, (7.27)
а на концах отрезка условиям
u (a) = u (b) = 0. (7.28)
Задача (7.27), (7.28) имеет следующее содержание. Между точками
x = a и x = b натянута упругая струна, находящаяся под действием внешней изгибающей нагрузки. f (x) — величина нагрузки, а u (x) — прогиб струны в безразмерных единицах.
2) Двухточечная краевая задача для линейного дифференциального уравнения второго порядка
 (7.29)
(7.29)
 (7.30)
(7.30)
Метод прогонки
Рассмотрим частный случай задачи (7.29), (7.30)
 (7.31)
(7.31)
 (7.32)
(7.32)
Введем сетку:  . Обозначим через ui приближенные значения u (x) в узлах сетки. Рассмотрим уравнение (7.31) во внутренних узлах
. Обозначим через ui приближенные значения u (x) в узлах сетки. Рассмотрим уравнение (7.31) во внутренних узлах  и заменим производную второго порядка разностной формулой (5.11):
и заменим производную второго порядка разностной формулой (5.11):
 . (7.33)
. (7.33)
Тогда из (7.31), (7.32) получим для определения ui систему линейных уравнений
 (7.34)
(7.34)
Система (7.34) при p (x) ≥ 0 имеет решение. Доказательство этого утверждения можно найти в [1].
Система (7.34) представляет собой систему линейных уравнений с трехдиагональной матрицей
 (7.35)
(7.35)
и для её решения применим метод прогонки, который фактически является методом исключения неизвестных Гаусса.
1. Прямой ход прогонки. Запишем первое уравнение (7.35) в виде
 (7.36)
(7.36)
Подставив (7.36) во второе уравнение (7.35) и упростив выражения, увидим, что можно для ui получить формулы
 (7.37)
(7.37)
Из последнего уравнения (7.35), учитывая (7.37) при  , получим
, получим
 (7.38)
(7.38)
2. Обратный ход прогонки. После вычисления прогоночных коэффициентов можно найти значения решения задачи. Формула (7.38) дает значение  :
:
 (7.39)
(7.39)
Остальные значения вычисляем в обратном порядке
 (7.40)
(7.40)
Пример 7. 6. Решить краевую задачу методом прогонки
 .
.
Решение в программе Excel. Выберем N = 10, т.е. шаг h = π/10 ≈ 0,31415926.
Составим таблицу значений аргумента x, функций p (x) и f (x), вычислим прогоночные коэффициенты и приближенные значения искомого решения по формулам (7.36) — (7.40). В таблице 7.11 приведен фрагмент листа Excel с результатами вычислений.
1) Заполним столбцы A 1: A 15, B 1: B 15 и строку A 4: H 4 как в таблице 7.11. При заполнении столбца значений переменной x можно ввести 0 в ячейку B 5, 3,1415926 в ячейку B 6, затем выделить B 5: B 6 и маркером заполнения протянуть до ячейки B 15.
2) Присвоим имена a, b и h ячейкам B 1, B 2, B 3 соответственно с помощью команды «Вставка — Имя — Присвоить».
Приведем содержимое для остальных ячеек, которые содержат формулы.
3) В столбце для значений p (x), т.е. в ячейках C 5: C 16 записываем единицы, так как p (x) = 1.
4) В диапазоне D 5: D 16 вводим формулу =-2*SIN(x), так как
f (x) = – 2sin x. Для этого достаточно ввести эту формулу в ячейку D 5 и протянуть D 5 маркером заполнения до D 15.
5) В ячейку E 5 введем число 0, а в ячейку E 6 — формулу
=1/(2+C6*h^2-E5) и протянем ячейку E 6 маркером заполнения до E 13. В ячейку E 14 запишем число 0.
6) В ячейку F 5 введем число 0, в ячейку F 6 вводим формулу
=(a-D6*h^2)/(2+C6*h^2-E5), и в ячейку F 7 введём =(F6-D7*h^2)/(2+C7*h^2-E6) и протянем ячейку F7 маркером заполнения до F 14.
7) Вычислим решение. В ячейку G 14 введем =F14, в ячейку G 13 введем формулу =E13*G14+F13 и протянем G 13 вверх до ячейки G 6.
8) Для проверки правильности вычислений вычислим в столбце H 5: H 15 значения точного решения задачи  . В ячейку H 5 введем формулу =sin(x) и протянем ячейку H 5 до H 15.
. В ячейку H 5 введем формулу =sin(x) и протянем ячейку H 5 до H 15.
Как видим из таблицы, полученные приближенные значения имеют абсолютную погрешность не более 0,01.
Таблица 7.11
| A | B | C | D | E | F | G | H | |
| 1 | a= | 0 |
|
|
|
|
|
|
| 2 | b= | 0 |
|
|
|
|
|
|
| 3 | h= | 0,31415926 |
|
|
|
|
|
|
| 4 | i | x | p(x) | f(x) | alfa | beta | ui | sin(x) |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 |
| 6 | 1 | 0,31415926 | 1 | -0,61803 | 0,476486 | 0,029064 | 0,310289 | 0,309017 |
| 7 | 2 | 0,62831852 | 1 | -1,17557 | 0,616443 | 0,089439 | 0,590204 | 0,587785 |
| 8 | 3 | 0,94247778 | 1 | -1,61803 | 0,674649 | 0,168077 | 0,812347 | 0,809017 |
| 9 | 4 | 1,25663704 | 1 | -1,90211 | 0,702224 | 0,249857 | 0,954971 | 0,951057 |
| 10 | 5 | 1,5707963 | 1 | -2 | 0,71609 | 0,320271 | 1,004116 | 1 |
| 11 | 6 | 1,88495556 | 1 | -1,90211 | 0,723272 | 0,367423 | 0,954971 | 0,951057 |
| 12 | 7 | 2,19911482 | 1 | -1,61803 | 0,727048 | 0,383239 | 0,812347 | 0,809017 |
| 13 | 8 | 2,51327408 | 1 | -1,17557 | 0,72905 | 0,363988 | 0,590204 | 0,587785 |
| 14 | 9 | 2,82743334 | 1 | -0,61803 | 0 | 0,310289 | 0,310289 | 0,309017 |
| 15 | 10 | 3,1415926 | 1 | -1,1E-07 |
|
|
| 5,36E-08 |
Рассмотрим ещё один пример простой краевой задачи, решение которой получим с помощью той же таблицы Excel.
Пример 7. 7. Решить краевую задачу методом прогонки

Решение в программе Excel. Выберем шаг h = 0,1, т.е. разделим отрезок [1, 2] на N = 10 частей. Откроем файл с решением примера 7.4 и внесем в таблицу изменения. Эти изменения не касаются столбцов E, F и G, в которых записаны формулы (7.27) — (7.31) метода прогонки.
Так как a = 2, b = 12 и h = 0,1, в ячейки B 1: B 3 вводим числа 2, 12 и 0,1.
Отметим те изменения, которые не видны явно в таблице 7.12.
В столбце для значений p (x), т.е. в ячейках C 5: C 16 записываем нули, так как p (x) = 0.
В ячейку D 5 вводим формулу =6*x+2, так как f (x) = 6 x + 2, и протянем ячейку D 5 до D 15.
В ячейку H 5 введем формулу =x^3+x^2 и протянем ячейку H 5 до H 15.
Результаты приведены в таблице 7.12.
Таблица 7.12
| A | B | C | D | E | F | G | H | |
| 1 | a= | 2 |
|
|
|
|
|
|
| 2 | b= | 12 |
|
|
|
|
|
|
| 3 | h= | 0,1 |
|
|
|
|
|
|
| 4 | i | x | p(x) | f(x) | alfa | beta | ui | x^3+x^2 |
| 5 | 0 | 1 | 0 | 8 | 0 | 0 |
| 2 |
| 6 | 1 | 1,1 | 0 | 8,6 | 0,5 | 0,957 | 2,54100000 | 2,54100000 |
| 7 | 2 | 1,2 | 0 | 9,2 | 0,666667 | 0,576667 | 3,16800000 | 3,16800000 |
| 8 | 3 | 1,3 | 0 | 9,8 | 0,75 | 0,359 | 3,88700000 | 3,88700000 |
| 9 | 4 | 1,4 | 0 | 10,4 | 0,8 | 0,204 | 4,70400000 | 4,70400000 |
| 10 | 5 | 1,5 | 0 | 11 | 0,833333 | 0,078333 | 5,62500000 | 5,62500000 |
| 11 | 6 | 1,6 | 0 | 11,6 | 0,857143 | -0,03229 | 6,65600000 | 6,65600000 |
| 12 | 7 | 1,7 | 0 | 12,2 | 0,875 | -0,135 | 7,80300000 | 7,80300000 |
| 13 | 8 | 1,8 | 0 | 12,8 | 0,888889 | -0,23378 | 9,07200000 | 9,07200000 |
| 14 | 9 | 1,9 | 0 | 13,4 | 0 | 10,469 | 10,46900000 | 10,46900000 |
| 15 | 10 | 2 | 0 | 14 |
|
|
| 12 |
Точное совпадение решения системы уравнений (7.34) со значениями решения краевой задачи (7.31), (7.32) объяснятся следующим обстоятельством. Разностная формула для производной второго порядка (7.33) дает точное значение (!) для кубических функций.






