Задача Коши для системы дифференциальных уравнений

Метод Рунге-Кутта применим и к задаче Коши для системы m дифференциальных уравнений с m неизвестными функциями

 

                           (7.18)

                   (7.19)

 

Приведем для задачи (7.18), (7.19) расчетные формулы метода Рунге-Кутта четвёртого порядка. Пусть требуется найти систему m функций 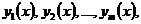 удовлетворяющих в интервале (x ₀, X) дифференциальным уравнениям (7.18), а в точке x _{0 —} начальным условиям (7.19). Предположим, что отрезок [ x ₀, X ] разбит на N частей

 

 

Тогда каждую l -ую функцию y_l (x) можно приближенно вычислять в точках x_{i +1} по формулам Рунге-Кутта

 

  (7.20)

 

Здесь через y_{l , i} мы обозначили приближенное значение функции y_l (x) в точке x_i.

Обращаем внимание на порядок вычислений по формулам (7.20). На каждом шаге сначала вычисляются коэффициенты K_{l , i} в следующем порядке

 

K _1,1, K _2,1, …, K_{m ,1},

K _1,2, K _2,2, …, K_{m ,2},

K _1,3, K _2,3, …, K_{m ,3},

K _1,4, K _2,4, …, K_{m ,4},

 

и лишь затем приближенные значения функций y _{1, i +1}, y _{2, i +1},…, y_{m , i +1}.

  Пример 7.4. Решить на отрезке [1, 2] задачу Коши

 

Решение в программе Excel. Точным решением задачи является система функций .

Разделим отрезок [1, 2] на N = 10 частей. Тогда шаг равен h = 0,1.

Число неизвестных функций m = 3. Число коэффициентов K_{l , i} равно 12. Создадим функции для вычисления правых частей f_l (x, y ₁, y ₂, y ₃) системы дифференциальных уравнений и коэффициентов K_{l , i}:

 

Function f_1(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

f_1 = 2 * x * y_1 / y_2

End Function

Function f_2(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

f_2 = 8 * y_3 / (3 * y_2)

End Function

Function f_3(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

f_3 = 3 * y_3 / y_1

End Function

Function K_1_1(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

K_1_1 = f_1(x, y_1, y_2, y_3)

End Function

Function K_2_1(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

K_2_1 = f_2(x, y_1, y_2, y_3)

End Function

Function K_3_1(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3)

K_3_1 = f_3(x, y_1, y_2, y_3)

End Function

Function K_1_2(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K11 = K_1_1(x, y_1, y_2, y_3)

K21 = K_2_1(x, y_1, y_2, y_3)

K31 = K_3_1(x, y_1, y_2, y_3)

K_1_2 = f_1(x + h / 2, y_1 + h * K11 / 2, y_2 + h * K21 / 2, y_3 + h * K31 / 2)

End Function

Function K_2_2(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K11 = K_1_1(x, y_1, y_2, y_3)

K21 = K_2_1(x, y_1, y_2, y_3)

K31 = K_3_1(x, y_1, y_2, y_3)

K_2_2 = f_2(x + h / 2, y_1 + h * K11 / 2, y_2 + h * K21 / 2, y_3 + h * K31 / 2)

End Function

Function K_3_2(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K11 = K_1_1(x, y_1, y_2, y_3)

K21 = K_2_1(x, y_1, y_2, y_3)

K31 = K_3_1(x, y_1, y_2, y_3)

K_3_2 = f_3(x + h / 2, y_1 + h * K11 / 2, y_2 + h * K21 / 2, y_3 + h * K31 / 2)

End Function

Function K_1_3(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K12 = K_1_2(x, y_1, y_2, y_3, h)

K22 = K_2_2(x, y_1, y_2, y_3, h)

K32 = K_3_2(x, y_1, y_2, y_3, h)

K_1_3 = f_1(x + h / 2, y_1 + h * K12 / 2, y_2 + h * K22 / 2, y_3 + h * K32 / 2)

End Function

Function K_2_3(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K12 = K_1_2(x, y_1, y_2, y_3, h)

K22 = K_2_2(x, y_1, y_2, y_3, h)

K32 = K_3_2(x, y_1, y_2, y_3, h)

K_2_3 = f_2(x + h / 2, y_1 + h * K12 / 2, y_2 + h * K22 / 2, y_3 + h * K32 / 2)

End Function

Function K_3_3(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K12 = K_1_2(x, y_1, y_2, y_3, h)

K22 = K_2_2(x, y_1, y_2, y_3, h)

K32 = K_3_2(x, y_1, y_2, y_3, h)

K_3_3 = f_3(x + h / 2, y_1 + h * K12 / 2, y_2 + h * K22 / 2, y_3 + h * K32 / 2)

End Function

Function K_1_4(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K13 = K_1_3(x, y_1, y_2, y_3, h)

K23 = K_2_3(x, y_1, y_2, y_3, h)

K33 = K_3_3(x, y_1, y_2, y_3, h)

K_1_4 = f_1(x + h, y_1 + h * K13, y_2 + h * K23, y_3 + h * K33)

End Function

Function K_2_4(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K13 = K_1_3(x, y_1, y_2, y_3, h)

K23 = K_2_3(x, y_1, y_2, y_3, h)

K33 = K_3_3(x, y_1, y_2, y_3, h)

K_2_4 = f_2(x + h, y_1 + h * K13, y_2 + h * K23, y_3 + h * K33)

End Function

Function K_3_4(ByVal x, ByVal y_1, ByVal y_2, ByVal y_3, ByVal h)

K13 = K_1_3(x, y_1, y_2, y_3, h)

K23 = K_2_3(x, y_1, y_2, y_3, h)

K33 = K_3_3(x, y_1, y_2, y_3, h)

K_3_4 = f_3(x + h, y_1 + h * K13, y_2 + h * K23, y_3 + h * K33)

End Function

 

Введем эти функции в программу Excel. Для этого с помощью меню «Сервис — Макросы — Редактор Visual Basic» откроем окно редактора и выполним команду «Insert — Module» и далее вводим описания функций.

После этого переходим в окно программы Excel и введем данные и формулы, как показано в таблице 7.9. Строки 1 и 2 и столбец A заполняем как в таблице. В ячейки B 3, C 3 и D 3 вводим начальные значения функций.

Ячейке B 1 присвоим имя h. В следующие ячейки введем указанные формулы и маркером заполнения копируем их вниз до строки 13 (табл. 7.8):

 

Таблица 7.8

Ячейка	Формула
B4	=B3+h*(K_1_1(A3;B3;C3;D3)+2*K_1_2(A3;B3;C3;D3;h) +2*K_1_3(A3;B3;C3;D3;h)+K_1_4(A3;B3;C3;D3;h))/6
C4	=C3+h*(K_2_1(A3;B3;C3;D3)+2*K_2_2(A3;B3;C3;D3;h) +2*K_2_3(A3;B3;C3;D3;h)+K_2_4(A3;B3;C3;D3;h))/6
D4	=D3+h*(K_3_1(A3;B3;C3;D3)+2*K_3_2(A3;B3;C3;D3;h) +2*K_3_3(A3;B3;C3;D3;h)+K_3_4(A3;B3;C3;D3;h))/6
E3	=A3
F3	=2*A3^2
G3	=3*A3^3

 

В результате вычислений в столбцах B, C и D получаем приближенные значения функций y ₁, y ₂, y ₃.

Таблица 7.9

	A	B	C	D	E	F	G
1	h=	0,1			Точные решения
2	xi	y1i	y2i	y3i	y1=x	y2=2x^2	y3=3x^3
3	1	1	2	3	1	2	3
4	1,1	1,100004	2,419978	3,992938	1,1	2,42	3,993
5	1,2	1,200008	2,879958	5,183862	1,2	2,88	5,184
6	1,3	1,300012	3,379938	6,590769	1,3	3,38	6,591
7	1,4	1,400016	3,919918	8,231656	1,4	3,92	8,232
8	1,5	1,50002	4,499897	10,12452	1,5	4,5	10,125
9	1,6	1,600025	5,119874	12,28735	1,6	5,12	12,288
10	1,7	1,700029	5,779848	14,73815	1,7	5,78	14,739
11	1,8	1,800034	6,479821	17,49492	1,8	6,48	17,496
12	1,9	1,90004	7,21979	20,57564	1,9	7,22	20,577
13	2	2,000045	7,999757	23,99832	2	8	24

 

Если потребуется решить другую задачу для системы с тремя неизвестными функциями, то достаточно изменить описания функций — правых частей и ввести новые начальные условия и шаг.