Для метода Рунге-Кутта применимо правило Рунге для оценки погрешности. Пусть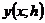 
приближенное значение решения в точке x, полученное по формулам (7.12), (7.13) или (7.14) с шагом h, а p — порядок точности соответствующей формулы. Тогда погрешность 
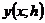значения можно оценить, используя приближенное значение 
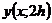решения в точке x, полученное с шагом 2 h
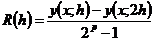, (7.15)
где p = 2 для формул (7.12), (7.13) и p = 4 для (7.14). Уточненное решение запишется в виде
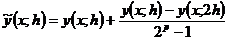. (7.16)
В алгоритмах с автоматическим выбором шага предварительно задают погрешность в виде положительного параметра ε, и на каждом этапе вычисления следующего значения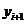 
подбирают шаг h такой, что выполняется неравенство
. (7.17)
Пример 7.3. Найти методом Рунге-Кутта с точностью ε = 10–8 решение задачи Коши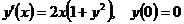 
в точке x = 1. Точным решением является функция 
.
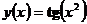Решение в программе Excel. Создадим функцию для вычисления правой части уравнения 
.
Function fxy(ByVal x, ByVal y)
fxy = 2 * x * (1 + y ^ 2)
End Function
Функция для применения метода Рунге-Кутта четвертого порядка с автоматическим выбором шага может быть записана в следующем виде:
Function Runge_Kutta(ByVal x0, ByVal y0, ByVal x, ByVal eps)
n = 2: erry = 1: y2h = Runge_Kutta4(x0, y0, x, n)
While Abs(erry) > eps
n2 = 2 * n: yh = Runge_Kutta4(x0, y0, x, n2)
erry = (yh - y2h) / 15: n = 2 * n: y2h = yh
Wend
Runge_Kutta = yh + erry
End Function
Здесь используется функция Runge_Kutta4(x0, y0, x, eps), созданная при решении задачи из примера 7.2. Если данная задача решается в том же файле, что и пример 7.2, то необходимо изменить функцию fxy(x, y) и добавить функцию Runge_Kutta(x0, y0, x, eps). Если используется новый файл, то необходимо заново создать все три функции
fxy(x, y), Runge_Kutta4(x0, y0, x, n), Runge_Kutta(x0, y0, x, eps).
Напомним, ключевое слово ByVal используется в описаниях функций для того, чтобы при обращении к данным функциям параметры передавались по значению, т.е. в вызвавшей программе эти переменные сохранят свои значения.
Теперь для решения задачи составим таблицу 7.6:
Таблица 7.6
| A | B | C | D | |
| 1 | xi | yi | y(x) | Ошибка |
| 2 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1,557407808 | 1,557407725 | 8,34673E-08 |
В ячейках C 2, C 3 вычислены значения точного решения задачи Коши.
В ячейке B 3 записана формула =Runge_Kutta4(A2;B2;A3;64). Здесь параметр n = 64 найден подбором так, чтобы погрешность в ячейке D 3 стала меньше, чем 10–8.
Заменим в ячейке B 3 формулу, т.е. введем =Runge_Kutta(A2;B2;A3;0,00000001). Использование метода с автоматическим выбором шага дает следующую таблицу 7.7:
Таблица 7.7
| A | B | C | D | |
| 1 | xi | yi | y(x) | ошибка |
| 2 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1,557407725 | 1,557407725 | 7,14521E-10 |
Более высокая точность последнего результата объясняется тем, что в методе с автоматическим выбором шага учитывается поправка по формулам Рунге (7.15), (7.16).
Составим программы на C ++ для решения задачи Коши методом Рунге-Кутта:
#include <iostream.h>
#include <math.h>
double f(double x,double y);
typedef double (*PF)(double,double);
double RK4(PF f,double x0, double y0,double x, const int n);
double RK4_eps(PF f,double x0, double y0,double x,double eps);
int main(){
double x0, x, y1, y2, eps, y0; PF pf; int n;
cout << "\n x0 = "; cin >> x0; cout << "\n y0 = "; cin >> y0;
cout << "\n n = "; cin >> n; cout << "\n x = "; cin >> x;
pf = f; y1 = RK4(pf,x0,y0,x,n);
cout << "\n n = "<<n<<" y("<<x<<") = " << y1;
cout << "\n eps = "; cin >> eps;
y2 = RK4_eps(pf,x0,y0,x,eps);
cout << "\n eps = "<<eps<<" y("<<x<<") = " << y2;
cout << "\n Press any key & Enter "; cin >> n; // pause
return 0;
}
double f(double x,double y){
double r; r = 2*x*(1+y*y);
return r;
}
double RK4(PF f,double x0, double y0,double x, const int n){
double h,k1,k2,k3,k4,y1,y2; int i;
h = (x-x0)/n; y1 = y0;
for(i = 1;i<=n;i++){ k1 = f(x0, y1); k2 = f(x0+h/2,y1+h*k1/2);
k3 = f(x0+h/2,y1+h*k2/2); k4 = f(x0+h,y1+h*k3);
y2 = y1+h*(k1+2*k2+2*k3+k4)/6; x0 = x0+h; y1 = y2; }
return y2;
}
double RK4_eps(PF f,double x0, double y0,double x,double eps){
typedef double (*PY)(double,double);
double erry,yh,y2h; int n; PY py;
n = 2; py = f; y2h = RK4(py,x0,y0,x,n);
do{ n = 2 * n; yh = RK4(py,x0,y0,x,n); erry = (yh-y2h)/15;
y2h = yh; }while(fabs(erry) > eps); yh = yh + erry;
return yh;
}
Приведем результаты вычисления решения задачи Коши
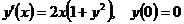
в точке x = 1:
Значение y1(1) = 1.55743 получено программой RK4(f, x0, y0, x, n) при
n = 10, а y2(1) = 1.55741 — программой RK4_eps(f, x0, y0, x, eps) с автоматическим выбором шага при eps = 0.00000001.
