Основные понятия, законы и формулы
1. При испарении жидкости может наступить такое состояние, при котором число молекул, вылетающих в единицу времени с открытой поверхности жидкости, будет равно числу молекул, влетающих в нее обратно. Между паром и жидкостью устанавливается подвижное — динамическое равновесие. Плотность пара над жидкостью и давление, производимое паром на стенки сосуда (упругость пара), при динамическом равновесии не меняются и имеют для данной жидкости при данной температуре максимальное значение.
Пар, давление и плотность которого имеют наибольшее значение при данной температуре, называют насыщающим. Иначе, насыщающим называют пар, находящийся в динамическом равновесии со своей жидкостью.
Пар, давление и плотность которого меньше давления и плотности насыщающего пара при данной температуре, называют не насыщающим.
2. Пары, отделенные от жидкости (при неизменной массе), обладают следующими свойствами:
а) При изотермическом увеличении объема, занимаемого насыщающим паром, или при его изохорическом нагревании насыщающий пар переходит в ненасыщающий.
б) При изотермическом сжатии ненасыщающего пара или при его изохорическом охлаждении ненасыщающий пар становится насыщающим.
Температуру, при которой пар становится насыщающим в результате изохорического охлаждения, называют точкой росы. При охлаждении пара ниже точки росы начинается конденсация пара в жидкость.
в) С достаточно хорошим приближением можно считать, что ненасыщающие пары подчиняются всем основным законам идеальных газов (3.1)–(3.4).
г) Параметры каждого состояния насыщающего пара связаны между собой уравнением Менделеева — Клапейрона.
Масса насыщающего пара m н.п, входящая в это уравнение, зависит от температуры и для двух различных состояний не может иметь одинакового значения.
Для определения давления насыщающих паров при данной температуре, если неизвестна их плотность, или же, наоборот, для определения плотности пара, если известно его давление, пользуются таблицами давления (упругости) насыщающих паров.
д) Так как в двух различных состояниях насыщающий пар имеет различную массу, параметры этих состояний законам идеальных газов (3.1)–(3.4) не подчиняются. Если же насыщающий пар переходит в ненасыщающий и его масса при этом не изменяется, то параметры состояний подчиняются всем законам идеальных газов.
е) Согласно закону Дальтона давление воздуха, содержащего водяной пар, складывается из давления сухого воздуха р с и давления паров воды р п, т. е. атмосферное давление равно:
3. Воздух содержащий водяной пар, называют влажным. О влажности воздуха можно судить или по величине давления, производимого паром, или по его плотности r п. Количество водяных паров (в граммах), содержащихся в 1 м3 воздуха, называют абсолютной влажностью. Отношение плотности r п водяного пара при данной температуре к плотности насыщенного пара r н.п. при этой же температуре называют относительной влажностью. Относительную влажность воздуха выражают обычно в процентах.
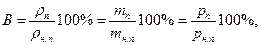
так как при одинаковой температуре
Решение задач. Примеры
1. Задачи на пары и влажность по своему решению принципиально почти не отличаются от задач на идеальные газы. Тем не менее они вызывают серьезные затруднения, связанные с неумением пользоваться уравнением газового состояния и попыткой искать решение путем логических рассуждений, что во многих случаях требует большой сообразительности. Особенно это относится к тем задачам, где вместо плотности насыщенного пара дается его давление.
Новым при решении задач на влажность является широкое использование таблиц упругости и плотности водяных паров и применение формулы относительной влажности. Из таблиц можно взять дополнительные данные к тем, которые известны по условию задачи, и составить вспомогательные уравнения, позволяющие вместе с основным уравнением газового состояния и законом Дальтона определить искомую величину.
Анализируя условие задачи на пары и влажность, всегда полезно иметь в виду следующее. Если задана температура насыщающего пара, то его давление и плотность при этой температуре можно найти в таблицах. Если же заданы температура и давление (плотность) насыщающего пара, то его плотность (давление) определяют из уравнения Менделеева – Клапейрона.
Давление насыщающих паров при температуре кипения жидкости равно атмосферному. Например, при температуре кипения воды (373 К) давление ее насыщающих паров равно нормальному атмосферному давлению (1.01·105 н/м2).
Если известна температура насыщающего пара Т 1 и его точка росы Т р, то с помощью таблиц можно определить абсолютную и относительную влажность воздуха при температуре Т 1, так как при температуре Т р это же количество пара будет полностью насыщать данное пространство. Порядок решения задач на влажность можно рекомендовать такой:
а) Установить число состояний газа, рассматриваемых в условии задачи, обратив особое внимание на то, дается ли чистый пар жидкости или смесь пара с сухим воздухом.
б) Для каждого состояния пара записать уравнение Менделеева – Клапейрона и формулу относительной влажности, если о. последней что-либо сказано в условии. Составить уравнение Менделеева – Клапейрона для каждого состояния сухого воздуха (если дается смесь пара с воздухом). В тех случаях, когда при переходах из одного состояния в другое масса пара не меняется, вместо уравнения Менделеева – Клапейрона можно использовать сразу объединенный газовый закон.
С учетом формулы влажности уравнение Менделеева – Клапейрона для пара можно записать в виде:
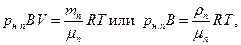
где р н.п. – давление, которое создавал бы пар, если бы при температуре Т он был насыщающим; ρ п – плотность пара.
в) Записать математически все дополнительные условия, связывающие величины, входящие в составленные ранее уравнения. Проверить число неизвестных в полученной системе уравнений и решить ее относительно искомой величины. Выписывая числовые значения заданных величин, нужно учесть сделанные выше замечания и использовать таблицу давления и плотности насыщающих паров при различных температурах.
Пример 1. Под колоколом насоса находится стакан, содержащий воду массой m =200 г. Насос откачивает воздух из-под колокола со скоростью u =50 л/мин. Через сколько времени вся вода испарится, если установившаяся под колоколом температура равна Т =280 К?
Решение. Если под колокол насоса поместить стакан с водой, то, спустя некоторое время, пространство под колоколом станет насыщенным водяными парами. При заданной температуре давление р н.п. и плотность ρ н.п пара можно считать известными, так как их значения могут быть найдены в таблицах.
Когда насос начнет работать, пары из-под колокола будут удаляться и их давление должно уменьшаться. Происходит это, однако, не сразу. Поскольку насыщающий водяной пар находится над водой и между молекулами воды и пара существует подвижное равновесие, уменьшение числа молекул пара, вызванное действием насоса, приводит к тому, что из жидкости начинает вылетать молекул больше, чем влетать в нее. Вследствие непрерывного испарения воды при работе насоса убыль молекул пара все время пополняется, в результате плотность пара, а следовательно, и давление некоторое время почти не изменяются. Само собой разумеется, что температура пара должна при этом поддерживаться постоянной.
Как только вся вода испарится, давление под колоколом начнет падать. Процесс откачки пара из-под колокола насоса до полного испарения воды удобно схематически представить так.
В сосуде находится насыщающий водяной пар, масса которого равна массе воды в стакане и давление которого при работе насоса остается неизменным. Температура пара, а значит, и давление, известны, и требуется определить время, необходимое для его удаления при заданной скорости откачки. Применяя к данному воображаемому состоянию насыщающего пара уравнение Менделеева – Клапейрона, можно определить объем пара, а затем и время, необходимое для его откачки, зная производительность насоса. Нетрудно заметить, что это время и будет равно искомому времени испарения воды под колоколом.
Предположим, водяной пар массой m при температуре Т насыщает пространство объемом V и производит давление р н.п. Тогда
(1)
Если насос, откачивая пар, захватывает объем V 0 за время τ 0, то производительность насоса (скорость откачки) будет равна:
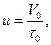(2)
и весь пар, находящийся в объеме V, насос откачает за время
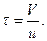(3)
Это и есть время испарения всей воды.
Давление насыщающих паров при Т =280 К находим из таблицы: р н.п.=7.5 мм рт. ст.= 103 н/м2.
Из уравнений (1)– (3) получим искомое время:
Пример 2. В запаянной трубке объемом V =0.4 л находится водяной пар под давлением р п=8.5·103 н/м2 при температуре Т п=423 К. Какое количество росы выпадает на стенках трубки при охлаждении воды до температуры Т н.п.=295 К?
Решение. В задаче рассматривают два состояния пара в запаянной трубке – до и после охлаждения. В первом состоянии при 423 К пар был ненасыщающим, поэтому при его изохорическом охлаждении, начиная с некоторой температуры (точки росы), пар станет насыщающим и дальнейшее понижение температуры до 295 К вызовет его частичную конденсацию.
Происходит ли конденсация пара при изохорическом понижении температуры от значения Т 1 до Т 2, если об этом не сказано в условии задачи, можно установить самим, зная плотность или давление пара. С помощью таблиц нужно только определить, будет ли температура росы Тр > T 2 или нет, В нашем примере это неравенство имеет место, следовательно, пар конденсируется.
Чтобы определить количество росы, выпавшей на стенках трубки, необходимо найти массу пара при каждой из заданных температур и вычесть из первого результата второй. Для нахождения самих масс удобно воспользоваться уравнением Менделеева – Клапейрона, составив его для каждого из двух состояний пара.
Обозначим параметры состояния пара до его охлаждения через p п, V, Т п и будем считать, что его масса равна m п. Тогда
(1)
После охлаждения и конденсации, когда пар в трубке будет насыщающим, его масса станет равной m н.п, а параметры примут значение p н.п, V и Т н.п. Для насыщающего дара
(2)
При составлении этого уравнения мы не учитывали объем, занимаемый каплями, и считали давление насыщенного пара известным, так как температура его Т н.п дана.
Для определения массы росы, выпавшей на стенках трубки, составляем вспомогательное уравнение:
(3)
где m – искомая масса росы. Этим уравнением условие задачи исчерпывается полностью.
Решая уравнения (1)–(3) совместно, находим:
Пример 3. В комнате размером V =10x5x3 м3 поддерживается температура Т 1=293 К; а точка росы равна Т 2=283 К. Определите относительную влажность воздуха и количество водяных паров, содержащихся в комнате.
Решение. Если воздух в комнате содержит некоторое количество водяных паров, то при понижении температуры до точки росы эти пары становятся насыщающими. В тех случаях, когда задана точка росы, как, например, в нашей задаче, можно рассмотреть два состояния пара в комнате: при данной температуре Т 1 и температуре росы Т 2. Каждое из этих состояний описывается уравнением Менделеева – Клапейрона и формулой относительной влажности. Давление насыщающих, паров можно считать при этом известным, так как известна их температура (точка росы).
Допустим, что пар находящийся в комнате объемом V, при температуре T 1 создает давление p 1 и имеет массу m п тогда
(1)
Если при этой температуре давление насыщающих паров равно р 1н, то относительная влажность воздуха в комнате
(2)
поскольку истинное давление паров в комнате – p 1. В случае понижения температуры до Т 2 (точки росы) пар в комнате стал бы насыщающим и его давление было бы равно р 2н. Для этого состояния пара мы могли бы записать:
(3)
так как масса пара в комнате остается неизменной.
В уравнениях (1)–(3) содержится три неизвестные величины – В, m п, которые требуется определить, и давление p 1. Решая уравнения совместно относительно искомых неизвестных, получим:
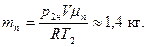
Пример 4. 1 м3 влажного воздуха при относительной влажности В =60%, температуре Т =293 К и нормальном атмосферном давлении имеет массу М =1.2004 кг. Определите давление насыщающего водяного пара при температуре Т.
Решение. Влажный воздух представляет смесь сухого воздуха и водяного пара. По условию задачи даются величины, характеризующие эту смесь в целом, и требуется определить параметр одного из газов, входящих в смесь, – давление насыщающего пара.
Для решения задачи нужно рассмотреть каждый компонент газа, составив для каждого из них уравнение состояния. Кроме того, необходимо будет учесть, что масса М и давление влажного воздуха р складываются соответственно из масс и давлений сухого воздуха и пара:
(1)
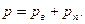(2)
Рассмотрим сначала воздух без пара. Обозначим параметры состояния воздуха в заданном объеме через р в, V, Т, тогда
(3)
где μ в=29 кг/кмоль—киломолекулярная масса сухого воздуха. Пар, находящийся в этом же пространстве, будет иметь давление р п, объем V и температуру Т. Для него
(4)
и, кроме того,
(5)
где p н.п – искомое давление насыщающих паров при температуре Т. Из уравнений (1)–(5) находим:
Пример 5. В сосуде находится воздух, температура которого Т 1=283 К и влажность В =60%. Как изменится влажность воздуха и его давление, если воздух нагреть до T 2=373 К и в три раза уменьшить объем? Начальное давление сухого воздуха p 1==3.85·104н/м2, давление насыщающих паров воды при 283 К равно р н1=1.2·103 н/м2.
Решение. Нам даны два состояния смеси сухого воздуха с паром при разных температурах. Как видно из условия задачи, в процессе нагревания сосуда меняются все три параметра состояния и воздуха, и пара. Чтобы выбрать исходные уравнения для решения задачи, надо прежде всего установить, изменяется ли масса пара при его переходе во второе состояние или нет. Сделать это можно следующим образом. С помощью объединенного газового закона надо найти давление р п2 пара при температуре Т 2=373 К и сравнить его с давлением насыщающего пара при этой температуре р н2=1.01·105 н/м2. Так как большего давления, чем р н2, пар при данной температуре иметь не может, то, если окажется, что р п2 > р н2, это будет означать, что происходила конденсация, если же р п2 < р н2, то при переходе во второе состояние масса пара не менялась — его недостаточно, чтобы создать давление р н2. Расчет показывает (предлагаем его сделать самим читателям), что в нашем примере р п2 < р н2, т. е. пар не конденсируется, и, следовательно, к параметрам пара применимо уравнение объединенного закона, поскольку масса газа остается одной и той же.
При составлении системы уравнений для нахождения изменения относительной влажности достаточно ограничиться (в данной задаче) лишь рассмотрением пара, так как все величины по условию задачи относятся только к нему.
Допустим, что в начальном состоянии при температуре Т 1 пар, находящийся во влажном воздухе, имел давление р п1 и объем V l, а после нагревания сосуда до температуры Т 2 — р п2 и V 2. Тогда согласно объединенному газовому закону должно быть:
(1)
Относительная влажность воздуха до нагревания:
(2)
после нагревания она станет равной:
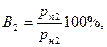(3)
Ее изменение
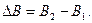(4)
Под р н1 и р н2 здесь подразумевается давление насыщающего пара при температурах Т 1 и Т 2.
Совместное решение уравнений (1)–(4) относительно Δ В при условии, что 3 V 2= V l, дает:
Знак «минус» означает, что В 2< B l т. к. во втором состоянии влажность воздуха уменьшилась.
Изменение Δ р полного давления влажного воздуха равно сумма изменений давлений сухого воздуха и пара:
. (5)
Так как масса воздуха не изменялась и воздух занимает тот же объем, что и пар, то
(6)
где p 2 — давление сухого воздуха после нагревания сосуда.
Решая совместно уравнения (1), (2), (5) и (6) относительно Δ р, получим:
Задачи к главе 4
4.1. Сколько молекул ртути может содержаться в 1 см3 воздуха в помещении, зараженном ртутью, при температуре 300 К, если давление насыщенного пара ртути при 300 К равно 0.36 н/м2?
4.2. Какое давление будет создавать водяной пар, насыщенный при 373 К, если в момент насыщения его отделить от воды и изохорически нагреть на 298 К?
4.3. Цилиндрический сосуд сечением 100 см снабжен поршнем массой 103.3 кг. Непосредственно под поршнем находится 0.8 г воды. На какое расстояние переместится поршень, придя в равновесие, если сосуд и воду нагреть до 423 К? Атмосферное давление нормальное, давление насыщающих паров воды при 423 К равно 4.75·105 н/м2.
4.4. Сосуд, снабженный поршнем, содержит водяной пар при температуре 323 К который производит давление 7.75·103 н/м2. Каково будет давление в сосуде, если объем, занимаемый паром, изотермически уменьшить вдвое? Давление насыщающих паров воды при 323 К равно 1.23·104 н/м2.
4.5. 
В цилиндре под поршнем площадью 100 см2 находится 18 г водяного пара при температуре 373 К. К поршню через систему блоков подвешен груз массой 50 кг (Рис. 4.1.). На какую высоту поднимется груз, если цилиндр охладить до 273 К? Атмосферное давление нормальное, массой поршня пренебречь. Давление насыщающих паров воды при 273 К равно 5.3·102 н/м2.
4.6. Закрытый цилиндрический сосуд высотой Н =1 м и сечением S =10-2 м2, расположенный вертикально, разделен легким поршнем, под которым находится вода массой m в=0,2 г. Над поршнем находится азот массой m а =6,14 г. Начальная температура сосуда Т 1 = 333 К. На сколько переместится поршень, если сосуд нагреть до Т 2=373 К? Давление насыщающих паров воды при 333 К равно рн.п.=0.22·105 н/м2.
4.7. Запаянную с одного конца трубку, содержащую некоторое количество воздуха, опустили в резервуар с водой. Длина подводной части трубки 2 Н =2м, уровень воды внутри трубки отстоит на расстоянии H от ее запаянного конца, начальная температура всей системы 273 К. Найдите положение уровня воды в трубке после нагревания всей системы до 373 К. Атмосферное давление нормальное, давлением паров воды при 273 К пренебречь.
4.8. При нормальном атмосферном давлении в сосуд вводят кислород О 2 и метан СН 4 в таком количестве, что парциальные давления газов оказываются равными. Сосуд закрывают и производят взрыв: СН 4 + 2 О 2= СО 2 + 2 Н 2 О. После этого сосуд охлаждают до начальной температуры. Зная, что давление насыщающих паров воды при этой температуре равно 2.24 кн/м2, определите установившееся давление в сосуде.
4.9. Сосуд объемом 1.25·10-3 м3 содержит сухой воздух при нормальных условиях. В сосуд вводят 0,9 г воды, закрывают его и нагревают до 363 К. Чему равно давление влажного воздуха в сосуде? Как изменится ответ, если взять сосуд емкостью 2.5·10-3 м3? Давление насыщающих паров воды при 363 К равно 7·104 н/м2.
4.10. В сосуде объемом V =1 м3 находится смесь воздуха с парами эфира. Внесенный в сосуд барометр при температуре Т ==303К показывает давление р =1.07·105 н/м2. Определите массу воздуха и эфира в сосуде, если известно, что конденсация паров в нем начинается при Т 0=273 К. Упругость насыщенного пара эфира при 273 К равна р оэ=24.4 кн/м2. Молекулярная масса эфира 74, воздуха 29.
4.11. В двух одинаковых сосудах объемом по 500 см3 каждый находится водород и кислород при температуре 293 К. Давление водорода 26.6 кн/м2, кислорода 53.2 кн/м2. Оба сосуда соединили между собой и, после того как газ перемешался, пропустили электрический ток, в результате чего гремучая смесь сгорела. Каким станет давление в сосудах после того, как установится первоначальная температура? Давление насыщающих паров воды при 293 К равно 2,32 кн/м2,
4.12. Найдите среднее расстояние между молекулами насыщенного водяного пара при 373 К. Во сколько раз это расстояние больше расстояния между молекулами воды при 273 К?
4.13. В цилиндре под легким незакрепленным поршнем находится насыщенный водяной пар объемом V =1 м3. Сколько льда, взятого при 273 К, надо бросить в сосуд, чтобы весь пар сконденсировался? Атмосферное давление нормальное. Удельная теплота парообразования воды при 373 К равна r= 2.26·106дж/кг, удельная теплота плавления льда λ = 3.34·105 дж/кг. Теплоемкостью и теплоотдачей цилиндра пренебречь.
4.14. В цилиндрическом сосуде под поршнем находятся пары воды в объеме υ=2·10-3 м3 при температуре Т =373 К и давлении р =105 н/м2. При постоянном внешнем давлении поршень опускают настолько, что объем уменьшается вдвое. Какое количество тепла надо отвести от сосуда для того, чтобы температура пара осталась постоянной? Объемом сконденсировавшейся воды пренебречь.
4.15. 4.15. Под невесомым поршнем в цилиндре имеется вода массой 1 кг при температуре 273 К. В воду опускают кусок раскаленного железа массой 1 кг, после чего поршень поднимается на 64 см. До какой температуры было нагрето железо? Атмосферное давление нормальное, удельная теплоемкость железа 500 дж/(кг·град), площадь поршня 0.1 м2. Теплоотдачей и теплоемкостью цилиндра пренебречь.
4.16. В цилиндре под поршнем в объеме 1.674·10-3м3 находится насыщенный водяной пар при температуре 373 К, масса пара 10-3 кг. Какую работу нужно совершить, чтобы изотермически сжать пар до полной конденсации в жидкость? При температуре 373 К плотность воды, находящейся под давлением ее насыщающего пара, равна 96 кг/м3.
4.17. Относительная влажность воздуха в помещении 63%, температура 18 °С. До какой температуры надо охладить блестящий металлический предмет, чтобы на его поверхности можно было наблюдать осаждение водяных паров?
4.18. Температура воздуха в комнате объемом 150 м3равна 6 °С, относительная влажность 80%. Сколько воды нужно испарить в этой комнате, чтобы при увеличении температуры до 18 °С относительная влажность стала равна 60%?
4.19. Относительная влажность воздуха вечером при температуре 16 °С равна 60%. Ночью температура воздуха понизилась до 4 °С и выпала роса. Сколько водяного пара сконденсировалось из 1 м3 воздуха?
4.20. В цилиндрическом сосуде под поршнем массой М =10 кг находится некоторое количество влажного воздуха при температуре Т =373 К. В положении равновесия поршень отстоит от дна на расстоянии h 1=2,20 м. Если цилиндр перевернуть вверх дном, поршень располагается на расстоянии h 2= 2.30 м от дна. Площадь поршня S =5·10-2м2, атмосферное давление p 0=105 н/м2. Насколько изменится относительная влажность воздуха в сосуде?
4.21. Смешали 1 м3 воздуха с влажностью 20% и 2 м3 воздуха с влажностью 30%. При этом обе порции были взяты при одинаковых температурах. Смесь занимает объем 3 м3. Определите относительную влажность смешанного воздуха.
4.22. Сколько теряет в своем весе шар объемом V =15 м3 при увеличении относительной влажности воздуха на Δ В =20% при температуре Т = 288 К? Давление насыщающего пара при 288 К равно р н.п=1.7 кн/м.
4.23. Давление воздуха при температуре 300 К и относительной влажности 70% равно 1.02·105 н/м2. Чему будет равно давление, если температура понизится до 270 К и относительная влажность станет 80% при неизменных остальных условиях? Давления насыщающего пара при указанных температурах равны соответственно 0.31·105 и 0.47·105 н/м2.
4.24. Колба объемом 100 см3 заполнена при 313 К воздухом с относительной влажностью 40%. Как надо изменить объем колбы, чтобы при понижении температуры до 293 К пар не конденсировался? Давление насыщающего пара воды при 313 К равно 7.3 кн/м2.
4.25. В сосуде объемом 0.1 м3 при температуре 303 К находится воздух с относительной влажностью 30%. Какова будет влажность воздуха в сосуде, если ввести 1 г воды, взятой при той же температуре? Давление насыщенных паров воды при 303 К равно 4.2 кн/м2. Решите задачу при условии, что сосуд имел объем 10-3м3.
4.26. Какой была относительная влажность воздуха при температуре Т 1=293 К, если при давлении р =6.06·103 кн/м2 точка росы этого воздуха равна Т 2=373 К. Давление насыщающих паров воды при температуре Т 1 равно р н.п=2.32 кн/м2.
Ответы и решения.
Глава 1. Теплота.
1.1. 33.40С. 1.2. ≈40С. 1. 3. 
1.4. 78 г. 1.5. 
1.6. 261 г. 1.7. 
1.8. ≈106 см3. 1.9. 00С; 400 г воды и 300 г льда. 1.10. 
. 1.11. Решение.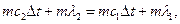 
отсюда 
. 1.12. 493 г воды и 207 г льда. 1.13. 314 дж. 1.14. 1.7·108 н/м2. 1.15. 112.5 г. 1.16. 00С; 28 г; 72 г; 100 г льда при –40С. 1.17. После 146-го. 1.18. 1.08 кг. 1.19. 32 кн. 1.20. 23 км/ч. 1.21. 2.8·105 кдж. 1.22. 1.68·10-2 дж. 1.23. 10.30С. 1.24. ≈8.1 кг. 1.25. 88%. 1.26. 8.3 кг. 1.27. 83.1 км. 1.28. 
1.29. 24.10С. 1.30. ≈2.4км/сек; 
1.31. 
1.32. 1600С; 402 дж. 1.33. Решение. Согласно закону сохранения импульса и закону сохранения энергии 
(1); 
(2); 
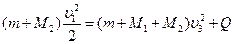(3). Из (1)–(3) 
