За счет этой теплоты внутренняя энергия молекул азота возрастает на величину
где 
– масса испарившегося азота; R – удельная теплота парообразования.
Согласно, закону сохранения и превращения энергии
. (1)
Проводя аналогичные рассуждения для льда, получим:
. (2)
Дополнительные условия позволяют записать:
(3)
Исключая из уравнений (I)–(3) неизвестные k и находим:
дж/кг.
Пример 5. Лед массой М = 1 кг при температуре 0°С заключен в теплонепроницаемый сосуд и подвергнут давлению р =6.9·107 н/м2. Сколько льда расплавится, если при. увеличении давления на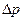 
=3.8·107н/м2 температура плавления льда понижается на 
=10С? Понижение температуры плавления от 0°С считать пропорциональным увеличению давления сверх атмосферного.
Решение. Если лед подвергнуть давлению больше атмосферного, температура его плавления понизится и такой, лед, находясь при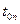 
=0°С, плавится, поглощая тепло из окружающей среды.
При достаточной теплоизоляции льда средой, отдающей тепло, служит сам лед. Работа, совершаемая внешними силами, идет в этом случае на перераспределение энергии между молекулами воды. Часть исходного количества льда растает, часть охладится до новой температуры плавления 
и система придет в равновесное состояние:
При отсутствии тепловых потерь количество- теплоты, выделенной при охлаждении не растаявшего льда от 0°С до температуры плавления , равно количеству теплоты, пошедшей на его частичное плавление
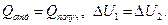
Температура плавления при давлении 
определяется из условия, что ее понижение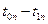 
пропорционально увеличению давления 
, т. е.
(1)
где k – коэффициент пропорциональности, зависящий от физических свойств вещества.
Вместе с уравнением теплового баланса это уравнение является основным соотношением для решения данной задачи.
При сжатии льда и понижении температуры плавления от 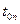до внутренняя энергия теплового движения молекул льда массой М уменьшится на
где с – удельная теплоемкость льда.
Так как система изолирована, то вся теплота, выделяющаяся при сжатии, идет на плавление льда массой m:
Согласно закону сохранения энергии
(2)
Кроме того, дополнительное условие позволяет записать
(3)
Решая уравнения (1)–(3) совместно относительно т и подставляя числовые значения, получим:
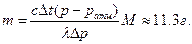
Пример 6. Некоторая установка, развивающая мощность N =30квт, охлаждается проточной водой, текущей по спиральной трубке сечением S =1 см2. При установившемся режиме проточная вода нагревается на =150С. Определите скорость воды 
, предполагая, что на нагревание воды идет 
=0.3 мощности.
Решение. В процессе работы установки часть механической энергии расходуется на нагревание проточной воды, охлаждающей установку. Так как теплообмен с окружающей средой не учитывается (Q =0), то указанная часть мощности установки идет на увеличение внутренней энергии воды и, согласно закону сохранения и превращения энергии, должно быть
Если за время 
в трубках нагревается вода массой m на градусов, то работа, совершенная за это время (при мощности N), и изменение внутренней энергии воды будут равны соответственно
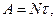
и 
где с – удельная теплоемкость воды.
Подставляя выражения для А и 
в исходное уравнение энергетического баланса, получим:
При течении потока по трубе сечением S масса жидкости 
, прошедшей через это сечение за время , равна:
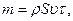
где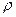 
– плотность жидкости; u — скорость течения.
С учетом этого выражения уравнение закона сохранения и превращения энергии в окончательном виде можно записать так:
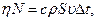
откуда
м/с.
Пример 7. Санки массой m =5 кг скатываются с горы, которая образует с горизонтом угол a=30°. Пройдя расстояние l =50 м, санки развивают скорость u =4.1 м/сек. Вычислите количество теплоты, выделенное при трении полозьев о снег.
Решение. При движении одного тела по поверхности другого часть механической энергии идет из-за трения на увеличение внутренней энергии соприкасающихся тел. Мерой изменения энергии здесь могут служить и работа А, и количество теплоты Q. Как А, так и Q показывают, на сколько возрастет внутренняя энергия беспорядочного движения молекул при изменении энергии направленного движения, вызванном трением санок о снег. Следует заметить, что работа силы трения скольжения всегда связана с нагреванием тел. Поскольку изменение внутренней энергии тел в процессе движения санок по условию задачи не рассматривается ( =0), то согласно (1.1) исходной формулой для решения задачи может служить уравнение
При его записи мы учли, что тепло отводится от системы (Q < 0) и работа совершается санками (А > 0).
Работу А, совершаемую внешними силами в системе санки – Земля, можно вычислить двумя способами: или с помощью закона сохранения энергии, или с помощью второго закона Ньютона. Проще воспользоваться первым способом. В системе санки — Земля на санки действуют две внешние силы: сила трения F тр и нормальная реакция опоры N. Так как N ^ u, то работа этой силы равна нулю и изменение механической энергии происходит лишь под действием силы трения, т. е. А = F тр.
Выбрав первое положение системы в начале движения санок, второе – в конце перемещения, можно записать:
Так как полная механическая энергия санок в первом и втором положениях соответственно равна:
то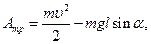 
и исходное уравнение можно переписать так:
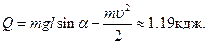
Пример 8. Свинцовая пуля, летящая со скоростью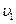 
=400 м/сек, попадает в стальную плиту и отскакивает от нее со скоростью 
=300 м/сек. Какая часть пули расплавится, если ее температура в момент удара была равна 
=107°С и на нагревание пули пошло =0.8 всей работы, совершаемой при ударе? Удельная теплоемкость и удельная теплота плавления свинца равны соответственно с=0.126·103 дж/(кг град), 
=25·103дж/кг.
Решение. В процессе удара пули о плиту происходит уменьшение кинетической энергии пули, вследствие чего увеличивается ее внутренняя энергия. Пуля нагревается до температуры плавления и частично плавится без теплообмена с окружающей средой (Q=0). Согласно закону сохранения и превращения энергии
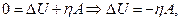
где – коэффициент, показывающий, какая часть механической энергии пошла на нагревание и агрегатное превращение свинца.
Если в момент удара пуля обладала кинетической энергией 
, а после удара 
(считаем, что расплавленный свинец находится внутри пули и отлетает вместе с ней), то работа силы сопротивления плиты при ударе равна:
При нагревании пули массой т от начальной температуры до температуры плавления 
=327°С и плавлении свинца массой 
внутренняя энергия пули возрастает на величину
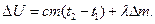
Подставляя выражения для А и в исходное уравнение, получим уравнение энергетического баланса в окончательном виде:
Отношение 
, показывающее, какая часть пули расплавилась, отсюда равно:
Задачи к главе 1.
1.1. Температура - термометра, погруженного в воду массой 6.7 г, повысилась на 14.6°С. Какова была температура воды перед измерением, если показание термометра равно 32.4°С? Теплоемкость термометра равна 1.92 дж/град.
1.2. Вода может находиться при температурах, меньших 0°С и больших 100°С. В калориметре с теплоемкостью 1.67 кдж/град находится 1 кг переохлажденной воды при температуре –10°С. Какая температура установится в калориметре, если в него влить 170 г воды, перегретой до 120°С?
1.3. В калориметре с теплоемкостью С находится вода массой М, нагретая до температуры . В калориметр опускают смесь латунных и алюминиевых опилок массой m, имеющую температуру . В результате этого температура воды повышается и становится равной 
. Определите количество латунных и алюминиевых опилок в смеси.
1.4. В литр воды при 20°С брошен комок мокрого снега массой 250 г. Когда весь снег растаял, общая температура стала равной 5°С. Определите количество воды в комке снега. Удельная теплота плавления снега 334 кдж/кг.
1.5. В калориметр, содержащий воду массой m при температуре T, опустили снег массой М при температуре – T. Спустя некоторое время τ наступило тепловое равновесие. Сколько воды окажется в калориметре через указанное время, если вода и снег будут иметь массы М и m и те же начальные температуры? Временем плавления пренебречь.
1.6. В латунный калориметр массой 125 г опускают кусок льда массой 100г. Температура калориметра и льда равна -20°С. Сколько воды при температуре 20°С надо добавить в калориметр, чтобы половина льда растаяла? Удельная теплоемкость латуни 0.38 кдж/(кг град), льда 2.1 кдж/(кг град), удельная теплота плавления льда 334 кдж/кг.
1.7. Железный шарик радиусом R, нагретый до температуры T, положили на лед, температура которого 0°С. На какую глубину шарик погрузится в лед? Теплопроводностью льда и нагреванием образовавшейся воды пренебречь. При расчете считать, что шарик погрузится в лед полностью.
1.8. В куске льда, находящемся при 0°С, сделано углубление, объем которого 160 см3. В это углубление влито 60 г воды, температура которой 75°С. Какой объем будет иметь свободное от воды углубление, когда вода остынет?
1.9. В чашке находится 500 г льда при 0°С. В чашку вливают 200 г воды, нагретой до температуры 80°С. Какова будет установившаяся температура и что будет находиться в чашке?
1.10. В закрытом сосуде с водой при температуре 0°С плавает лед массой М, в который вмерзла свинцовая дробинка массой m. Сколько тепла нужно подвести к системе лед – свинец, чтобы льдинка полностью погрузилась в воду? Плотности свинца, льда и воды равны соответственно 
, удельная теплота плавления льда λ.
1.11. На сколько изменяется удельная теплота плавления вещества при понижении температуры плавления на , если удельные теплоемкости вещества в жидкой и твердой фазе равны соответственно с 1 и с 2?
1.12. В сосуд, содержащий 200 г льда при температуре –15°С, влито 500 г воды, переохлажденной до температуры -15°С. Сколько получится льда и воды из такой смеси? Удельную теплоемкость воды и льда считать не зависящей от температуры.
1.13. Какое количество теплоты выделяется при замерзании 1 г воды, переохлажденной до –10°С?
1.14. Какому давлению были подвергнуты 20г льда, заключенного в теплонепроницаемую оболочку при 0°С, если при этом расплавилось 1.6 г льда и, кроме того, известно, что при увеличении давления на 1.4·107 н/м2 температура плавления понижается на 1°С? Считать, что понижение температуры плавления пропорционально повышению давления.
1.15. В калориметр, содержащий 100г льда при 0°С, впущен пар, имеющий температуру 100°С. Сколько воды окажется в калориметре непосредственно после того, как весь лед растает? Удельная теплота парообразования воды при 100°С равна 2.26·106 дж/кг.
1.16. Тонкая стеклянная пробирка, содержащая 100 г воды при температуре 20°С, опущена в дьюаровский сосуд, содержащий 50 г эфира при температуре 10°С. Какова будет температура оставшейся воды, когда весь эфир испарится? Что будет находиться в пробирке? Теплообменом с окружающей средой и стеклом пренебречь. Удельная теплоемкость жидкого и газообразного эфира 2.1 кдж/(кг град), его удельная теплота испарения 376 кдж/кг. Решите задачу при условии, что эфира было 120 г.
1.17. Кожух пулемета емкостью 3.88 л наполнен смесью воды с глицерином (75% воды по объему). Начальная температура смеси 10°С. После какого выстрела температура смеси достигнет 100°С? Каждый патрон содержит 3.2 г пороха, масса стального ствола 2.1 кг. На нагревание ствола пулемета и охлаждающей смеси расходуется 74% энергии. Теплота сгорания пороха 4.18·106 дж/кг, удельная теплоемкость глицерина 2.4 кдж/(кг град), стали – 0.46 кдж/(кг град). Плотность глицерина 1.26·103 кг/м3.
1.18. 1 г водорода, сгорая и превращаясь в воду, выделяет 142 кдж тепла. Сколько угля с теплотой сгорания 2.93·107 дж/кг надо сжечь для диссоциации 1 л воды, если из выделяемой углем теплоты используется 50%?
1.19. Следуя по течению, пароход прошел расстояние между двумя пунктами в 150 км за 10 ч 40 мин. То же расстояние против течения пройдено за 18 ч 50 мин. Чему равна сила сопротивления воды движению парохода, если он сжигал 120 кг угля в час? Коэффициент полезного действия паровой машины 10%. Теплота сгорания угля 2.9·107 дж/кг.
1.20. Поезд массой 1500 т идет по горизонтальному пути со скоростью 60 км/ч. Паровоз сжигает при этом 1600 кг угля в час. Какую скорость разовьет поезд при тех же условиях на пути с уклоном вверх 0.01? Коэффициент полезного действия паровых машин паровоза равен 12%.
1.21. Какое количество тепла выделяется при полном торможении поезда, идущего со скоростью 54 км/ч под уклон 0.01, если масса поезда равна 2000 т? Силу сопротивления считать пропорциональной нормальному давлению. Коэффициент сопротивления 0.05.
1.22. Стеклянный шарик объемом 0.2 см3 равномерно падает в воде. Сколько тепла выделится при перемещении шарика на 6 м? Плотность стекла 2.4 г/см3,
1.23. На сколько градусов нагреется медная пластинка размером 2x6 см при нарезании в ней резьбы с шагом 0.75 мм, если при нарезке к воротку нужно приложить момент силы в 4.9нм? Размером отверстия пренебречь. Плотность меди 8.9 г/см3, удельная теплоемкость 376 дж/(кг град).
1.24. Грузовой автомобиль, оборудованный газогенераторным двигателем мощностью 92 квт, имеющим коэффициент использования тепла 0.18, работает в полную нагрузку. Определите массу древесных чурок с теплотворной способностью 1.25·107 дж/кг, необходимых для пробега пути в 1 км со скоростью 1.8 км/ч.
1.25. Трансформатор, погруженный в масло, вследствие перегрузок начинает греться. Каков его коэффициент полезного действия, если при полной мощности 60 квт 40 кг масла в течение 4 мин нагрелись на 20 град? Удельная теплоемкость масла 2.1 кдж/(кг град). Количеством тепла, идущим на нагревание металла трансформатора и его обмотки, пренебречь.
1.26. Вращающийся в подшипнике вал диаметром 10 см делает 200 об/мин и давит на подшипник с силой 12 кн. Определите часовой расход масла, пропускаемого для охлаждения подшипника, если температура масла при подаче равна 12, а при выходе 60°С. Коэффициент трения 0,015, удельная теплоемкость масла 1.7 кдж/(кг град).
1.27. Заряд 305-миллиметровой пушки содержит 155 кг пороха. Масса снаряда 446 кг. Какова максимальная дальность полета снаряда, если к.п.д. орудия равен 28%? Теплота сгорания пороха.4.18· 106 дж/кг сопротивление воздуха не учитывать.
1.28. Тележка с песком массой М катится без трения по горизонтальным рельсам со скоростью 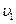. Пуля массой m, выпущенная со скоростью совпадающей по направлению с 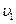попадает в тележку и застревает в ней. Сколько механической энергии перешло при ударе в тепло?
1.29. Свинцовая пуля массой 10 г, летящая горизонтально со скоростью 300 м/сек, попадает в неподвижный стальной кубик массой 100 г, лежащий на гладком горизонтальном столе. Какова будет температура тел после удара? Удар считать абсолютно неупругим, температура пули в момент удара 25°С, кубика 15°С. Потерями тепла пренебречь. Удельная теплоемкость стали 0.46 кдж/(кг град), свинца 0.125 кдж/(кг град).
1.30. С какой скоростью должны лететь навстречу друг другу две одинаковые льдинки, имеющие температуру T =–10°С, чтобы при ударе они обратились в пар? Удельные теплоемкость и теплота плавления льда равны соответственно с=2.9 кдж/(кг град) и =334 кдж/кг. Удельная теплота парообразования воды при, 100°С 
=2.26·106 дж/кг. Решите задачу при условии, что Массы льдинок равны и 
.
1.31. Горизонтально летящая пуля массой попадает в деревянный шар, лежащий на полу, и пробивает его. Определите, какая часть энергии перешла в тепло, если начальная скорость пули 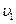скорость после вылета из шара , масса шара М, Трения между шаром и полом отсутствует, траектория пули проходит через центр шара.
1.32. Из винтовки произведен выстрел вертикально вверх Свинцовая пуля массой 10 г вылетает со скоростью 300 м/сек и на высоте 500 м попадает в такую же пулю, летящую горизонтально со скоростью 284 м/сек. На сколько градусов нагреются пули после абсолютно неупругого удара и какова будет их суммарная кинетическая энергия, если в момент удара их температура была одинаковой? Сопротивлением воздуха пренебречь.
1.33. На идеально гладкой горизонтальной поверхности лежит доска массой M 1 на которой находится брусок массой M 2. В брусок попадает пуля массой m, летящая горизонтально со скоростью u, и застревает в нем. Вследствие удара брусок проходит по доске некоторое расстояние и затем под влиянием сил трений перестает двигаться относительно доски. Определите механическую энергию, перешедшую в тепло из-за трения между бруском и доской,
Глава 2. ТЕПЛОВОЕ РАСШИРЕНИЕ ТВЕРДЫХ И ЖИДКИХ ТЕЛ
Основные понятия, законы и формулы
1. Для большинства тел вблизи 0°С существует температурный интервал, в пределах которого любой линейный размер тел изменяется по закону
, (2.1)
где l – длина или какой-либо линейный размер тела при температуре t, l 0 – при 0°С, а a– коэффициент линейного расширения при начальной температуре.
2. Если линейные размеры тела изменяются по закону (2.1), то для каждого сечения тела
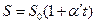, (2.2)
где S – площадь данного сечения при температуре t; S 0 – при 0°С, a' – средний коэффициент увеличения площади. При небольших температурах с достаточной степенью точности можно считать, что a'=2a.
3. При увеличении линейных размеров по закону (2.1) объем тела меняется вследствие нагревания по закону
, (2.3)
где β – средний коэффициент объемного расширения. При небольших температурах β =3a.
4. В случае теплового расширения тел их плотность изменяется по закону
(2.4)
где r — плотность тела при температуре t; r 0—плотность при 0°С.
Решение задач. Примеры
1. Решение задач о тепловом расширении тел целиком основано на применении одной из формул (2.1)—(2.4) к каждому состоянию нагреваемого тела. Если в задаче рассматривается не одно, а несколько тел, эти формулы записываются для каждого тела отдельно. Все вместе они образуют полную систему уравнений, решение которых позволяет найти искомую величину. В комбинированных задачах формулы теплового расширения являются лишь частью системы уравнений, описывающих данное явление; вторую часть, как правило, составляют формулы калориметрии и гидростатики. При составлении уравнений теплового расширения тел особое внимание нужно обратить на следующее.
а) В формулах (2.1)—(2.4) под l 0, S 0 и V 0 подразумевают значения длины, площади и объема при 0°С, а не при начальной температуре тела, отличной от нуля; это связано с тем, что табличные коэффициенты линейного и объемного расширения определяются как изменения единицы длины или объема тела, взятого при 0°С, при нагревании на 1 град. Если за начальную температуру принять не 0°С, а произвольную температуру, относительное удлинение, рассчитанное на один градус, – коэффициент линейного расширения (а также и коэффициент объемного расширения) – в каждом случае будет разным и не таким, как при 0°С.
Чтобы найти связь между длинами (площадями, объемами) при температурах t 1 и t 2. нужно из уравнений
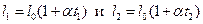
исключить t 0. В результате получим:
или приближенно:
(2.5)
если пренебречь членами, содержащими a в более высокой степени, чем первой. Практически такое приближение вполне оправдано, так как для большинства твердых тел a очень мало.
Проводя вычисления в задачах на тепловое расширение тел, нужно иметь в виду, что 
и 
если х <<1 и y <<1 использование этих формул значительно облегчает вычисления и упрощает математические выкладки. В частности, при небольших температурах t, таких, что βt <<1, можно с достаточной степенью точности считать, что плотность тел r ≈ r 0(1- βt).
б) Формулы (2.2) и (2.3) справедливы как для сплошных тел, так и для тел, в которых имеется полость или отверстие.
2. Задачи на тепловое расширение тел удобнее решать по следующей схеме:
а) Для каждого теплового состояния каждого тела записать соответствующую формулу теплового расширения.
б) Если в задаче наряду с расширением тел рассматриваются другие процессы, сопутствующие расширению, – теплообмен, изменение гидростатического давления жидкости или выталкивающей силы, то к уравнениям теплового расширения надо добавить формулы калориметрии и гидростатики.
