в) Выписать значения заданных величин и, проверив число неизвестных в полученной системе уравнений, решить ее относительно искомой величины.
Пример 1. Какую длину l 0c и l 0М при температуре 0°С должны иметь стальной и медный стержни, чтобы при любой температуре разность их длин составляла Δ l= 10 см? Коэффициент линейного расширения стали aс=1.2·10-5 град-1, меди aм=1.7·10-5 град-1.
Решение. Рассмотрим два тепловых состояния стального и медного стержней: при начальной температуре t 0=0°С и при некоторой произвольной температуре t. Обозначим длину стального стержня при температуре t через l с, медного — через l м, тогда
(1)
(2)
Дополнительное условие позволяет записать:
в частности,
(3)
Вычитая из второго уравнения первое и раскрывая скобки, получим:
откуда с учетом соотношений (3) имеем:
Из этого и второго равенства (3) для искомых длин получаем:
Пример 2. Стальная и латунная полоски толщиной H =0.2 см каждая склепаны на концах так, что при температуре t 1=20°С они образуют плоскую биметаллическую пластинку. Каков будет средний радиус изгиба биметаллической пластинки при t 2=100°С? Коэффициенты линейного расширения стали и латуни равны aс=1.2·10-5 град-1; aл=1.9·10-5 град-1.
Решение. Так как коэффициенты линейного расширения латуни и стали неодинаковы (aл>aс), то при нагревании биметаллической пластинки латунная полоска удлинится больше стальной и вся пластинка изогнется.
Если при температуре t 1 длина средней линии латунной пластинки была равна t 1л, при температуре t 2- t 2л, то, пользуясь приближенной формулой (2.5), можно записать:
(1)
где Δ t = t 2- t 1 – приращение температуры.
Для стальной пластинки аналогично предыдущему получим:
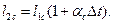
поскольку приращение температуры здесь то же самое.
Чтобы определить средний радиус изгиба R, будем считать, что концы пластинок при деформации не смещаются относительно друг друга и толщина их настолько мала, что ее изменением при нагревании можно пренебречь по сравнению с изменением длины.
Как видно из чертежа (рис. 2.1), l 2л и l 2с связаны с радиусом изгиба R уравнениями:
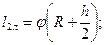(3)
(4)
где φ — угол между торцевыми поверхностями биметаллической пластинки.
Составленная система уравнений полностью отражает все условия задачи и позволяет определить искомую величину.
Решая уравнения (1)—(4) совместно относительно среднего радиуса R кривизны
биметаллической пластинки, получим:
Пример 3. Латунная шкала ртутного барометра выверена при 0°С. При температуре t 1=20 °С барометр показывает давление р 6=760 мм рт. ст. Каково истинное атмосферное давление р а при этой температуре? Расширением стекла пренебречь. Коэффициенты линейного расширения латуни и объемного расширения ртути соответственно равны α= 1.9∙10-5 град-1 и β =1.8∙10-4 град-1
Решение. Если шкалу барометра выверить при какой-либо температуре, например при 00С, то при всякой другой температуре его показания не будут соответствовать наружному давлению. Объясняется это тем, что с повышением температуры плотность ртути уменьшается и при неизменном атмосферном давлении высота столба ртути в барометрической трубке возрастает. Кроме того, шкала, по которой отсчитывают высоту столба, удлиняется и цена одного деления становится больше значения, указанного на шкале. Чтобы определить истинное давление, показание барометра нужно привести к той температуре, при которой его шкала выверена, — в данном случае к 0°С. Делается это сравнительно просто: находят число делений шкалы, в которые укладывается высота измеряемого ртутного столба, рассчитывают по формуле теплового расширения новую цену деления и по этим данным определяют действительную длину ртутного столба. Зная эту длину и плотность ртути при температуре измерений, можно вычислить и само атмосферное давление.
Если при температуре t 1= 20 °С ртуть в барометрической трубке достигла высоты h1 (n-го деления шкалы), то показания барометра равны:
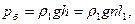(1)
где ρ 1 – плотность ртути при температуре t 1; l 1 - цена одного деления шкалы. Так как расстояние l 0 между двумя соседними рисками на шкале выверено и равно единице (1 мм) лишь при 0°С, то l 1 будет больше цены деления l 0, указанной на шкале.
Если коэффициент линейного расширения латуни равен α, то
и в единицах длины l 0 высота ртутного столба при температуре t равна:
(2)
Так как по условию задачи атмосферное давление не изменяется, то 
и в то же время 
, откуда
(3)
где ρ 0 – плотность ртути при 0°С; H 0 – высота, на которую поднялся бы столб ртути при температуре 0°С, Плотность ртути
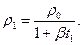(4)
Из уравнений (1)—(4) получим:
Пример 4. При температуре t 1=10 °С железная канистра вмещает V 1=20 л бензина и оказывается наполненной целиком. На сколько изменится масса канистры с бензином, если ее внести в помещение, где температура равна t 2=30 °С? Коэффициенты объемного расширения железа и бензина β ж=3.6∙10-5 град-1 и β б==10-3 град-1, плотность бензина ρ 0=0.8 г/см3.
Решение. Вследствие теплового расширения канистры и бензина объем их при нагревании увеличивается. Коэффициент объемного расширения жидкостей всегда больше коэффициента объемного расширения твердых тел, поэтому при нагревании на одинаковое число градусов приращение объема бензина будет больше приращения объема сосуда и часть бензина из него выльется. Чтобы определить искомое изменение массы канистры с бензином, нужно вычислить массу бензина в канистре при начальной и комнатной температурах и из первого результата вычесть второй. Масса самой канистры при этом не изменится. Для нахождения массы бензина при указанных температурах необходимо найти его плотность при этих температурах, а также объем канистры.
Если при температуре t 1 канистра и, следовательно, бензин имеют объем V 1, а при температуре t 2 – объем V 2, то
(1)
Плотность бензина при температурах t 1 и t 2 соответственно равна:
(2)
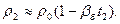(3)
Массы бензина в канистре при этих температурах равны:
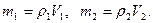(4)
Решая уравнения (1)–(4) совместно и пренебрегая членами, содержащими коэффициенты объемного расширения в степени выше первой, из-за их малости, получим:
Пример 5. В жидкости взвешивают стальной шарик. Первое взвешивание проводилось при температуре t 1 и вес вытесненной жидкости оказался равным Р 1; второе взвешивание провели при температуре t 2 и вес вытесненной жидкости был равен Р 2. Определите коэффициент объемного расширения жидкости, если коэффициент объемного расширения стали равен β.
Решение. Вследствие теплового расширения тел, взвешиваемых в жидкости, вес вытесненной жидкости при разных температурах будет разным. Он будет определяться плотностью жидкости при данных температурах и объемом тел, погруженных в жидкость. Если при температуре t 1 в жидкость полностью погрузить шарик объемом V 1, то вес вытесненной жидкости будет равен:
(1)
Плотность жидкости ρ 1 и объем стального шарика V 1 при температуре t 1 могут быть выражены через их значения при 0°С:
(2)
(3)
где β ж – коэффициент объемного расширения жидкости. Для температуры t 2 мы имеем соответственно:
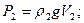(4)
(5)
(6)
Решая уравнения (1)—(6) относительно β ж, находим:
Члены, содержащие коэффициенты теплового расширения в степени выше первой, здесь отброшены из-за их малости.
Задачи к главе 2
2.1. Длина стержня при температуре 0°С равна 1000 мм, при температуре 100 °С – 1002 мм, при температуре красного каления – 1011.6 мм. Определите температуру красного каления.
2.2. Колесо локомотива имеет диаметр 1 м при 0°С. На сколько отличаются расстояния, пройденные поездом за 1 ч зимой и летом при температурах –25 °С и +25 °С, если в обоих случаях двигатель развивал 480 об/мин? Коэффициент линейного расширения стали 1.2∙10-5 град-1.
2.3. При температуре t °C показание ртутного барометра с латунной шкалой равно n. Каково будет показание барометра при 0°С? при – t °С? Атмосферное давление во всех случаях одинаково. Коэффициент линейного расширения латуни α, коэффициент объемного расширения ртути β.
2.4. Два секундных маятника, первый – медный, второй – железный, отбивают секунды при температуре –2 °С. На сколько секунд отстанет в сутки медный маятник от железного, если температура помещения поднимется до 18 0С? Коэффициенты линейного расширения меди и железа равны соответственно 1.7∙10-5 град-1 и 1.2∙10-5 град-1.
2.5. Часы снабжены латунным маятником. Сравнивая показания этих часов с показанием точных часов, заметили, что при 0°С они спешат на 7 сек в сутки, а при температуре 20 °С отстают в сутки на 9 сек. Определите коэффициент линейного расширения латуни, а также ту температуру, при которой маятниковые часы будут идти правильно.
2.6. При нагревании железного шара до температуры 800°С его поверхность увеличилась на 1 см. Определите диаметр шара при температуре 20 °С. Коэффициент линейного расширения железа 1.2∙10-5 град-1.
2.7. Никелевый брусок массой 740 г и длиной 22.2 см при температуре 50 °С опущен в калориметр с теплоемкостью 21 дж/град, содержащий 145 г воды при 0 0С. Когда температура установилась, то оказалось, что длина бруска уменьшилась на 0.13 мм. Определите удельную теплоемкость никеля. Коэффициент линейного расширения никеля 1.8∙10-5 град-1.
2.8. В центре стального диска имеется отверстие, диаметр которого при 0°С равен 4.99 мм. До какой температуры следует нагреть диск, чтобы в его отверстие начал проходить шарик диаметром 5 мм? Коэффициент теплового расширения стали равен 1.1∙10-5 град-1.
2.9. В железнодорожную цистерну при температуре +25 °С было налито 20 т бензина. На сколько уменьшится объем этого бензина у места слива, если температура воздуха в этом месте равна –20 °С? Коэффициент объемного расширения бензина равен 10-3 град-1.
2.10. Емкость железного сосуда при температуре 10 °С равна 2 л. Какова будет масса ртути в сосуде при температуре 25 °С? Коэффициент линейного расширения железа 1.2∙10-5 град-1, коэффициент объемного расширения ртути 1.8∙10-1 град-1.
2.11. При температуре t 1 стержни с коэффициентами линейного расширения α 1 и α 2 имеют одинаковую длину, при температуре t 2 одинаковыми оказываются их объемы. При какой температуре будут одинаковы площади поперечного сечения стержней?
2.12. В стеклянный цилиндр налита ртуть массой 1 кг. Остальную часть объема цилиндра занимает воздух, причем оказывается, что объем пространства над ртутью остается постоянным при всех температурах от 0 до 100 °С. Определите объем цилиндра. Коэффициент линейного расширения стекла равен 0.9∙10-5 град-1, коэффициент объемного расширения ртути – 1.8∙10-4 град
2.13. Стеклянный сосуд весит Р 0. Этот же сосуд, наполненный ртутью, при 0°С весит Р 1. Если сосуд нагреть до температуры t, то часть ртути выливается и вес сосуда с ртутью оказывается Р 2. Чему равен коэффициент объемного расширения стекла? Коэффициент объемного расширения ртути β.
2.14. Медный брусок, имеющий температуру t 1 сложен вместе с алюминиевым бруском, имеющим температуру t 2 и такую же массу, что и медный. Каково будет относительное изменение общего объема брусков, после того как температура выравнится?
2.15. В наполненном сосуде содержится керосин массой М к и кусок железа массой М ж. Если всей системе сообщить количество теплоты Q, то из сосуда будет выливаться керосин объемом V. Определите коэффициент объемного расширения железа. Теплоемкостью и расширением сосуда пренебречь. Работой расширения пренебречь.
2.16. Стальной брусок плавает в сосуде со ртутью в вертикальном положении. При температуре 0°С в ртуть погружена 0.577 часть всего объема бруска. На сколько изменится погруженная часть объема бруска, если систему нагреть до 100 °С? Коэффициент линейного расширения стали 1.2∙10-5 град-1, коэффициент объемного расширения ртути 1.8∙10-5 град-1.
2.17. Кусок латуни при 20 °С весит в керосине 0.77 н. Найдите объем этого куска при температуре 100 °С. Плотности латуни и керосина при 20 °С равны 8.5 г/см3 и 0.8 г/см3, коэффициент теплового расширения латуни равен 1.9∙10-5 град-1.
2.18. Вес куска металла, погруженного в известную жидкость, уменьшается на Р 1 при температуре t 1 и на Р 2 при температуре t 2. Определите коэффициент линейного расширения металла.
2.19. Стальной шарик массой m =100 г опущен на нити в керосин. На сколько изменится натяжение нити, если всю систему нагреть от t 1 = 20° С до t 2 = 50 °С? Плотности стали и керосина при 0°С равны ρ ос=7.9 г/см3, ρ ок=0.8 г/см3. Коэффициенты теплового расширения α – 1.2∙10-5 град-1, β =∙10-3 град-1.
2.20. На сколько надо увеличить внешнее давление, чтобы сохранить постоянным объем ртути при нагревании ее от 0 до 10 °С если известно, что с увеличением давления на 1 атм объем ртути уменьшается на 3.9∙10-6 части того объема, который она занимала при 0°С?
2.21. Какое количество теплоты надо затратить на единицу массы металлического шара радиусом R, чтобы увеличить его объем на z % по отношению к объему шара при 0°С? Атмосферное давление равно р, удельная теплоемкость металла с, коэффициент линейного расширения α.
2.22. Два кубика с массами m 1 и m 2 стоят на теплопроводящей подставке. На сколько изменится общая теплоемкость кубиков, если один из них положить на другой? Первый кубик железный, второй — медный.
Глава 3. ГАЗЫ
Основные понятия, законы и формулы
1. Состояние любого тела характеризуют совокупностью нескольких физических величин, называемых параметрами состояния. Важнейшими параметрами состояния газа являются его объем V, давление р и температура Т.
Состояние газа, при котором все его параметры при неизменных внешних условиях остаются постоянными сколь угодно долго, называют равновесным. Процессы, состоящие из непрерывной последовательности равновесных состояний, называют равновесными. Параметры состояния газов, находящихся в равновесных состояниях, связаны между собой уравнением состояния F (р, V, Т) = 0.
Самый простой вид уравнение состояния имеет для идеальных газов. Идеальными называют газы, молекулы которых взаимодействуют друг с другом лишь при соударениях (отсутствует межмолекулярное притяжение и отталкивание) и объем молекул ничтожно мал по сравнению с объемом, занимаемым газом. Кроме того, предполагают, что соударение молекул происходит по законам абсолютно упругого удара. Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше их давление и выше температура.
2. Для идеальных газов имеют место следующие экспериментальные законы.
Закон Бойля — Мариотта:
(3.1)
Из этого закона вытекает, что для двух произвольных состояний газа при указанных условиях справедливо равенство:
(3.1’)
Закон Гей-Люссака:
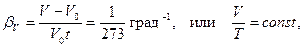(3.2)
если 
и m = const.
Согласно выражению (3.2) при соблюдении указанных ограничений для двух произвольных состояний
(3.2’)
Закон Шарля:
(3.3)
если 
и m = const.
Согласно закону Шарля для двух произвольных состояний:
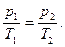(3.3’)
Соотношения (3.1), (3.2) и (3.3) можно рассматривать как уравнения состояния идеального газа соответственно при изотермическом, изобарическом и изохорическом процессах, когда из трех параметров газа изменяются два.
3. Из опытных законов (любых двух) для идеальных газов вытекает объединенный газовый закон (уравнение Клапейрона):
(3.4)
откуда следует, что при переходе газа из одного состояния в другое, когда меняются все три его параметра, должно быть:
(3.4’)
4. Молекулярной массой М данного вещества называют массу m х молекулы этого вещества, выраженную в углеродных единицах массы (у.е.м.). За углеродную единицу массы принята 1/12 часть массы m С самого легкого изотопа углерода:
Так же определяют и атомную массу А, но только под m х тогда подразумевают массу атома.
Киломолем называют такое количество вещества, масса которого μ, в килограммах численно равна молекулярной массе (μ = М) этого вещества.
Согласно закону Авогадро в одном киломоле (килоатоме) любого вещества содержится N А=6.02∙1026 молекул (атомов).
При нормальных условиях (р =1.01∙105 н/м2; Т =273 К) один киломоль идеального газа занимает объем υ0=22.4 м3/кмоль.
Если газ с киломолекулярной массой μ имеет массу m и содержит N молекул, то в нем содержится число киломолей ν, равное
(3.5)
Согласно (3.5) масса одной молекулы
При нормальных условиях объем идеального газа равен
(3.6)
Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, давление смеси газов равно сумме давлений, производимых каждым газом в отдельности, если бы он один занимал весь сосуд (закон Дальтона):
Если за первое состояние принять состояние идеального газа с параметрами р, V, Т, а за второе – его состояние при нормальных условиях, то согласно уравнению (3.4'):
Отсюда с учетом соотношений (3.6) и (3.5):
или
(3.7)
где величина 
имеет для всех идеальных газов одинаковое значение и называется универсальной газовой постоянной. Числовое значение газовой постоянной равно:
Уравнение (3.7) называют уравнением Менделеева – Клапейрона. Его можно представить в виде:
где ρ – плотность газа при данной температуре Т, а также
где 
– концентрация молекул; 
– постоянная Больцмана.
5. Если температура идеального газа массой m изменяется на Δ T, внутренняя энергия газа изменяется на величину
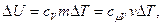(3.8)
где cv – удельная теплоемкость газа при постоянном объеме и сμV – молярная теплоемкость газа при постоянном объеме – теплоемкость, рассчитанная на киломоль газа.
Если при постоянном давлении р газ нагревается от температуры T 1 до температуры T 2, то его объем возрастает от V 1 до V 2 и газ совершает работу
(3.9)
Применяя уравнение (3.7) для каждого из двух состояний газа, формулу работы можно представить в виде:
(3.10)
Если в процессе расширения к газу подводится некоторое количество теплоты Q, то согласно закону сохранения и превращения энергии для изобарического процесса
(3.11)
Учитывая (3.8), (3.10) и (3.11) и что
(3.12)
можно записать:
(3.13)
6. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, равен:
(3.14)
где Q 1 и Q 2 – соответственно тепло, полученное от нагревателя и отданное холодильнику, T 1 и Т 2 – температуры нагревателя и холодильника.
Решение задач. Примеры
1. Основным уравнением, характеризующим состояние идеального газа, является уравнение Менделеева — Клапейрона. Составив это уравнение для каждого из рассматриваемых состояний газа и записав дополнительные условия в виде формул, можно сравнительно легко решить почти любую задачу на газы элементарного курса физики. Однако этот метод решения в ряде случаев усложняет решение и приводит к лишним математическим выкладкам, мало поясняющим физическую сущность явления.
Учитывая это, задачи на расчет параметров состояния газов можно разделить на две основные группы. К первой следует отнести такие задачи, где даны два или несколько состоянии газа, в которых его масса остается неизменной и к которым, следовательно, применимо уравнение объединенного газового закона (3.4).
Вторую группу составляют задали, в условии которых дана масса газа или рассматриваются такие процессы, в которых масса газа изменяется. При решении этих задач пользоваться объединенным газовым законом нецелесообразно, более удобно применять уравнение Менделеева — Клапейрона.
Решение задач на нагревание и работу газа при изохорическом и изобарическом процессе основано на первом начале термодинамики и формулах (3.9)—(3.10).
2. Если по условию задачи даны два состояния газа и при переходе газа из одного состояния в другое его масса не меняется, то для решения задачи можно рекомендовать следующую последовательность.
