Краткие теоретические сведения. В качестве параметра, характеризующего надежность, используется наработка до отказа

В качестве параметра, характеризующего надежность, используется наработка до отказа. Значение наработки до отказа, распределенное по заданному закону, моделируется с использованием ЭВМ на основе генератора случайной величины, распределенной равномерно в интервале I /6/. Для этой цели можно использовать, например, в программе EXCEL команду RND.

Последовательность значений наработки , распределенной по показательному закону с параметром (см. таблицу), может быть получена в соответствии с выражением

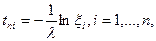(1)

где - случайная величина, распределенная равномерно в диапазоне I; -количество значений (образцов).

 

№ вар	Закон распределения	Кол-во образ- цов	Довери- тельная вероят- ность	Параметры распределения
Нормального в интерв.с границами	показательного
нижн. a, час	верх. b, час	,час-1
	Н П Н П Н П Н П Н П Н П Н П Н П		0,7 0,8 0,9 0,95 0,99 0,7 0,8 0,95 0,9 0,99 0,95 0,9 0,7 0,8 0,99 0,7	103 - 103 - 104 - 102 - 105 - 104 - 105 - 102 -	103 - 104 - 104 - 103 - 105 - 105 - 106 - 102 -	- 10-3 - 10-5 - 10-4 - 10-2 - 10-4 - 10-6 - 10-3 - 10-2

 

Последовательность значений наработки , распределенной по нормальному закону в заданном интервале величин, где . Таким образом, генерируя последовательности:

…

…

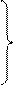
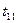
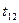
…………………… (2)

…

 

 

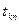
Можно промоделировать результаты эксперимента, распределенные по нормальному закону:

(3)

Значения (2) и (3) целесообразно занести в таблицу.

Чтобы изобразить законы распределения и 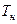, необходимо:

I) определить min и max значения в совокупностях, полученных с использованием (1) и (3), и после упорядочения элементов вычислить значения размаха и

;

2) вычислить длину интервала

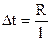, (4)

Где l-количество интервалов (зависит от желаемой точности представления результатов и количества образцов; в рассматриваемом случае l= );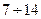

3) оценить на каждом интервале 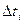экспериментальные значения плотности распределения наработки до отказа

,

Где - число отказов на интервале .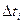

Нахождение границ доверительного интервала для средней наработки до отказа 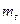при показательном распределении наработки до отказа производится с использованием распределения :

,

Где -суммарная наработка исследуемого изделия; k-число степеней свободы распределения:

 

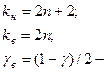
Значение вероятности того, что больше .

Значения и 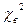берут из приложения 6 и /2/.

Нахождение границ доверительного интервала для средней наработки до отказа при нормальном распределении наработки до отказа производится с использованием распределения Стьюдента:

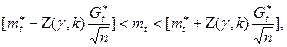
Где

Оценки математического ожидания и среднеквадратичного отклонения наработки до отказа; -квантиль распределения Стьюдента, который находят для вероятности (1+ )/2 и числа степеней свободы k=n-1 (см.Приложение 7 и /2/).

Контрольные вопросы

1 Какие виды испытаний на надежность вы знаете?

2 Как проводятся определительные испытания и обрабатываются их результаты?

3 Как проводятся контрольные испытания?

4 Охарактеризуйте особенности ускоренных испытаний.

5 Приведите примеры испытаний, основанных на анализе физики отказов и методах их прогнозирования.

6 Охарактеризуйте особенности испытаний на надежность АСУ.

 

Задачи

1. определить число изделий N, которые необходимо поставить на испытания по плану NUN, при условии, что допустимая ошибка в определении средней наработки до отказа T равна 20% от Т c доверительной вероятностью 0.96. наработка распределена по нормальному закону; предполагаемое значение Т=1000 часов.

2. определить продолжительность испытаний для изделий со средней наработкой до отказа Т=1000 часов при условии, что вероятность отказа изделия за время испытания должна быть не менее 0,9 (наработка распределена по показательному закону).

3. в результате наблюдения за эксплуатацией 100 неремонтируемых изделий зафиксированы отказы на 12 изделий. Значение наработки до отказа (в часах):58,110, 117,198,387,570,610,720,798,820,840,921. после двенадцатого отказа наблюдения прекращены. Оценить среднюю наработку до отказа изделий, предполагая показательное распределение наработки до отказа.

4. оценить вероятность отказа ремонтируемого изделия в течение заданной наработки, если известно, что в течение этой наработки произошло z=100 отказов. Под наблюдением находилось N=200 изделий.

 

 

БИБЛИОГРАРАФИЧЕСКИЙ СПИСОК

I. Глазунов Л.П., Грабовецкий В.П., Щербаков О.В. Основы надежности автоматических систем управления. Л.: Энергоатомиздат, 1984. 208 с.: ил.

2. Теория надежности радиоэлектронных систем в примерах и задачах / Под ред.

Г.В. Дружинина. М.: Энергия, 1976. 448 с.: ил.

3. Журавлев В.М., Вейс Л.Д., Гертель Е.О. Оценка надежности функционирования сложных систем управления при проектировании / Фрунзен. политехн. ин-т. Фрунзе, 1988. 115 с.: ил.

4. СТ СЭВ 544-77. Прикладная статистика: Ряды предпочтительных чисел для входных величин статистических таблиц. М., 1977.

5. Иыуду К.А. Надежность, контроль и диагностика вычислительных машин и систем. М.: Высшая школа, 1989. 216 с.: ил.

6. Голинкевич Т.А. Прикладная теория надежности. М.: Высшая школа, 1977. 160 с.: ил.

7. Надежность и эффективность в технике. Справочник: В 10 т. /Под ред. В.С. Авдуевского и др. М.: Машиностроение, 1986-1990.

 

 

Приложение I

Образец оформления

титульного листа отчета

o проделанной работе

 

 

Министерство народного образования

Кыргызской Республики

Кыргызский технический университет

 

 

Кафедра «Автоматическое управление

в технических системах»

 

 

Лабораторная работа

номер работы

тема работы

по дисциплине

название дисциплины

 

Выполнил ст. гр.

 

Ф.И.О.

Принял: преподаватель

Ф.И.О.

 

 

Бишкек

год

 

 

Приложение 2

Значение функции

U		I
0,0 0,I 0,3 0,5 0,7 0,9 I,0 I,I I,3 I,5 I,7 I,9 2,0 2,I 2,3 2,5 2,7 2,9 3,0 3,5 4,0	0,00000 II79I I9I46 3I594 34I34 433I9 47I28 482I4 0,49865	0,00399 I2I72 I9497 26II5 3I859 47I93 498I9	0,0II97 05I72 I2930 20I94 3238I 458I8 4834I 490I0	0,0I994 I3683 353I4 4II49 4744I 4906I 4946I 498I4 4993I	0,02790 I443I 2I566 4I466 44I79 46I64 49III 4985I	0,03586 I5I73 3389I 362I4 4I774 48I69 49I58 4986I

 

Приложение 3

Интенсивности отказов элементов

средние, максимальные и минимальные значения

интенсивности отказов

Наименование элементов	Интенсивность отказов
I

 

Резисторы 0,I59

I,0 - 0,00I

 

 

Композиционные 0,043

0,297-0,005

 

Пленочные 0,03

0,058-0,0I7

 

 

Металлопленочные 0,2

0,4-0,004

 

Переменные (потенциометры) 0,26

0,5-0,02

 

Проволочные 0,087

0,I97-0,046

 

Проволочные переменные 0,0I9

0,807-0,02

 

Угольные 0,045

0,888-0,005

 

Конденсаторы 0,I

2,385-0,00I

 

 

Бумажные 0,05

0,29-0,003

 

Керамические 0,I5

I,64-0,042

 

Слюдяные 0,075

0,I32-0,005

 

 

Стеклянные 0,06

0,87-0,0005

 

Танталовые 0,6

I,934-0,I08

 

Фольговые 0,054

0,076-0,045

 

Воздушные переменные 0,034

0,082-0,0I

 

Диоды

Германиевые 0,I57

0,678-0,002

 

Кремниевые 0,2

0,452-0,02I

 

Селеновые 0,2

0,6-0,II

Триоды (транзисторы)

Германиевые 0,9

I,9I-0,6

 

Германиевые мощные I,9I

 

Кремниевые 0,5

I,44-0,27

 

Кремниевые в ключевом режиме 0,7

0,848-0,25

Трансформаторы и дроссели

Трансформаторы звуковой частоты 0,02

0,04-0,0I

 

Высокочастотные 0,045

0,062-0,0I9

 

Импульсные 0,I7

0,285-0,03

 

Изоляторы 0,5

I,54-0,03

 

 

Регулировочные 0,I

0,3I-0,0035

 

Дроссели 0,34

2,22-0,07

 

Катушки индуктивности 0,02

I,0I8-0,00I

 

Реле, коммутационные и соединительные элементы

Реле 0,25/к.г.*

Разъемы штепсельные 0,062/ш*

Переключатели кнопочные 0,07/к.г.

Переключатели миниатюрные 0,25/к.г.

 

Переходные колодки 5,2

12,13-0,8

 

Гнезда 0,0I/ш

0,02/ш-0,002/ш

 

Клеммы, зажимы 0,0005

 

Тумблеры 0,06/к*

I,I23/к-0,0I5/к

 

Провода соединительные 0,0I5

0,I2-0,008

 

Кабели 0,475

2,2-0,002

 

Предохранители плавкие 0,5

0,82-0,30

 

Соединения пайкой 0,01

 

Изоляторы 0,5

I,54-0,03

 

Изолирующие шайбы, прокладки 0,00I

 

Источники питания

 

Аккумуляторы 7,2

19,0-0,35

 

Батареи однозарядные 30

 

 

Приложение 4

Значения коэффициентов h

 

Наименование элементов	Значения коэффициентов
Электрическая Нагрузка	тепловая нагрузка	вибрационная нагрузка
Транзисторы германиевые (типаП15,П16, П403)	1,2-1,4	0,9-1,5	0,8
транзисторы кремниевые	0,5	0,3-0,5	-
диоды германиевые	0,4	0,3-0,6	0,5
диоды кремниевые	-	0,2-0,6	-
резисторы непроволочные	1,2-2,0	0,3-0,8	0,3
конденсаторы кремниевые	3,0	0,5-0,85	0,3
конденсаторы бумажные	2,5-4	1,2-1,6	-
конденсаторы слюдяные	-	0,8-1,1	-
конденсаторы танталовые электролитические	-	0,5-0,6	-
туннельные диоды (ЗИ301)	1,25	1,25	0,5
кремниевые полупровод­никовые интегральные схемы (со степенью интеграции от 5 до 20 элементов)	0,5	0,5	-
реле	2,3	-	-
трансформаторы силовые	3,3	1,1	-

 

 

Приложение 5

Значения коэффициентов регрессии а, в модели для оценки ожидаемого числа ошибок в программах различного назначения

 

Тип программы	Коэффициенты
a1	а2	a3	a4	a5	a6	a7	a8
Управляющие		0,0405	0,171	0,430	0,036			-0,00186	4,00
Вывода			0,780				0,0218		4,56
Вычислитель -ные		0,024	0,412		0,416	0,016	0,082	-0,0026	6,34
Настройки		0,001	0,592				0,0625	-0,0036	3,04
Служебные	2,090	0,0374	0,628	0,102				-0,0133	1,64

 

 

Примечание: -среднеквадратичная погрешность регрессионных оценок числа ошибок в программе

 

Приложение 6

Квантили распределения хи-квадрат

Число	Вероятность
степеней	0,995	0,975	0,950	0,900	0,800	0,200	0,100	0,050	0,010	0,005
свободы
	20,7	24,4	26,5	29,1	32,3	47,3	51,8	59,3	63,7	66,8
	24,3	28,4	30,6	33,4	36,9	52,7	57,5	65,4	70,0	73,2
	28,0	32,4	34,8	37,7	41,4	58,2	63,2	71,4	76,2	79,5
	31,7	36,4	39,0	42,1	46,0	63,6	68,8	77,4	82,3	85,7
	35,5	40,5	43,2	46,5	50,6	69,0	74,4	83,3	88,4	92,0
	39,4	44,6	47,4	50,9	55,3	74,4	80,0	89,2	94,4	98,1
	43,3	48,8	51,7	55,3	59,9	79,7	85,5	95,0	100,4	104,2
	47,2	52,9	56,1	59,8	64,5	85,1	91,1	100,8	106,4	110,3
	51,2	57,2	60,4	64,3	69,2	90,4	96,6	106,6	112,3	116,3
	55,2	61,4	64,7	68,8	73,9	95,7	102,1	112,4	118,2	123,3

 

 

Приложение 7

Квантили распределения Стьюдента

 

Число Степеней свободы	Вероятность
0,8	0,9	0,95	0,975	0,995
	0,861	1,328	1,729	2,093	2,861
	,860	1,325	1,725	2,086	2,845
	,857	1,318	1,711	2,064	2,797
	,856	1,316	1,708	2,060	2,787
	,854	1,311	1,699	2,045	2,756
	0,854	1,310	1,697	2,042	2,750
	,851	1,303	1,684	2,021	2,704
	,849	1,298	1,676	2,002	2,678