Резервированные восстанавливаемые системы могут находиться в заданный момент времени в одном из нескольких состояний, которые отличаются друг от друга количеством исправных элементов. Процесс перехода системы из одного состояния в другое можно считать марковским, если время наработки до отказа и время восстановления распределены по показательному закону. Этот процесс можно представить в виде графа, отображающего количество состояний и интенсивности переходов между ними (см. рисунок) /2/.


На рисунке переходы, изображенные стрелками направо, означают отказы, и их интенсивность λi зависит от количества нагруженных элементов в i -том состоянии, а стрелки налево означают восстановление, и их интенсивность μi определяется количеством неисправных элементов и ремонтных бригад. Так, при ненагруженном резерве /I, 2/
λi =λ,+-
при нагруженном
λi= λ(k-i+1).
Восстановление может быть ограниченным (п < k), тогда при i ≥ n
μi=n μ,
при i<n
μi=i μ.
Если восстановление неограниченное, то естьn ≥ k, то
μi=i μ.
Вероятности пребывания системы в любом состоянииP0(t), P1(t), …,Pi(t), …, Pk+1(t)
можно найти из системы дифференциальных уравнений Колмогорова, количество которых равно количеству состояний. Уравнение для каждого состояния записывается в соответствии со следующим правилом:
- в левой части – производная вероятности рассматриваемого состояния по времени;
- в правой части - алгебраическая сумма, количество членов которой равно количеству стрелок, связанных с рассматриваемым состоянием; каждый член равен произведению интенсивности стрелки на вероятность того состояния, откуда стрелка выходит;
знак члена (+), если стрелка входит в рассматриваемое состояние, и (-), если она из него выходит.
Полученная система уравнений позволяет определить при заданных начальных условиях функции готовности Kг(t) и простоя Kп(t)
 ;
;
 .
.
Коэффициенты готовности K г и простоя Кп рассчитываются аналогично с учетом того, что в системе уравнений Колмогорова полагается dPi(t)/dt=0 (i=0,1,…,k+1), при этом для определения нетривиального решения полученная однородная система уравнений дополняется очевидным условием

Стационарные значения вероятностей P j можно определить непосредственно по схеме состояний, пользуясь cледующим правилом: необходимо идти по направлению стрелок из каждого крайнего состояния в j -тое по кратчайшему пути и перемножить все интенсивности переходов, соответствующие проходимым стрелкам. Таким образом проходят все пути из всех крайних состояний в каждое состояние системы.
Вероятность нахождения системы в j -том состоянии

где Δjи Δi- произведения интенсивностей переходов из всех крайних состояний соответственно в j -тое и i - тое при движении по кратчайшему пути в направлении стрелок; k+1 числосостояний системы.
Примечание. При разветвленной схеме состояний некоторые участки пути придется проходить несколько раз. При этом интенсивности переходов этих участков нужно учитывать только один раз.
Моделирование K г и K п произведите в диапазоне изменения до 0,5, которой является практически значимым.
Контрольные вопросы
I. Какие показатели надежности восстанавливаемых систем вы знаете?
2.Какие процессы называются марковскими?
3. Что такое схема состояний и каковы правила ее получения?
4. Опишите алгоритм составления системы дифференциальных уравнений Колмогорова и способы ее решения.
5. Какие еще методы оценки надежности сложных систем с восстановлением вы знаете?
Задачи
1.Восстанавливаемая система с показательными распределениями времени безотказной работы и времени восстановления имеет коэффициент готовности К г = 0,95. Вычислить вероятность безотказной работы системы в течение наработки (0,10) ч, если среднее время восстановления θ= 5 ч.
2.Определить величинуошибки Δ K г при вычислении вероятности нахождения восстанавливаемой системы в работоспособном состоянии в момент времени, равный средней наработке на отказ, по формуле для коэффициента готовности:

если оказалось, что K г= 0,6. Предполагается показательное распределение времени безотказной работы и восстановления; при t = 0 система работоспособна.
3. Восстанавливаема система с показательными распределениями времени безотказной работы и времени восстановления имеет коэффициент готовности К г= 0,9. Определить вероятность K г (t) нахождения системы в работоспособном состоянии в момент времени t= 50 ч, если наработка на отказ Т = 500 ч.
4. Преобразователь "параметр-код" состоит из рабочего блока и блока в ненагруженном резерве. Распределения времени до отказа и до восстановления- показательные с параметрами:  -3I/ч, μ = 0,8 I/ч. Требуется определить значения коэффициента простоя и во сколько раз уменьшается величина коэффициента простоя преобразователя при применении неограниченного восстановления по сравнению с ограниченным.
-3I/ч, μ = 0,8 I/ч. Требуется определить значения коэффициента простоя и во сколько раз уменьшается величина коэффициента простоя преобразователя при применении неограниченного восстановления по сравнению с ограниченным.
5.Система связи с подвижными объектами имеет нагруженный резерв. Интенсивность отказов основной и резервной подсистем равна λ I/ч. При отказе основной подсистемы автоматический переключатель ПУ включает резервный комплект. При отказе ПУ (интенсивность, отказов λ п.у. I/ч) становится невозможным подключение резервной подсистемы на место основной. Систему связи обслуживает одна ремонтная бригада. Интенсивность восстановления равна μ I/ ч. Требуется определить коэффициент простоя системы связи.
6. Система питания состоит из рабочего блока и двух резервных - в облегченном и ненагруженном резерве. Систему обслуживают две ремонтные бригады. Интенсивности отказов paбочего блока 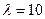 -2I/ч, блока в облегченном резерве
-2I/ч, блока в облегченном резерве 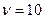 -3I/ч. Интенсивность восстановления каждой ремонтной бригадой μ =0,1 I/ч. Система предназначена для круглосуточной роботы. При выходе из строя рабочего комплекта на его место устанавливается комплект из облегченного резерва, а комплект ненагруженного резерва переводится в облегченный. При выходе из строя комплекта в облегченном резерве ненагруженный резерв также переходит в облегчений. Определить коэффициент простоя системы питания.
-3I/ч. Интенсивность восстановления каждой ремонтной бригадой μ =0,1 I/ч. Система предназначена для круглосуточной роботы. При выходе из строя рабочего комплекта на его место устанавливается комплект из облегченного резерва, а комплект ненагруженного резерва переводится в облегченный. При выходе из строя комплекта в облегченном резерве ненагруженный резерв также переходит в облегчений. Определить коэффициент простоя системы питания.
7. Вероятность безотказной работы ремонтируемого передатчика в течение 3 ч равна 0,997. Среднее время ремонта передатчика 2,5 ч. Определить коэффициент простоя передатчика.
8. Регистрирующее устройство содержит рабочий блок и блок в нагруженном резерве. Вероятность отказа блока в течение 25 часов Q(t)= 0,I. Ремонт производится одной бригадой с интенсивность μ = 0,2 I/ч. Определить коэффициент простоя регистрирующего устройства.
9. Усилитель состоит из двух равнонадежных блоков, для каждого из которых  -3I/ч. Имеется усилитель в ненагруженном резерве. Ремонт производит одна бригада, среднее время ремонта θ = 0,5 ч. Определить коэффициент простоя усилителя с резервом.
-3I/ч. Имеется усилитель в ненагруженном резерве. Ремонт производит одна бригада, среднее время ремонта θ = 0,5 ч. Определить коэффициент простоя усилителя с резервом.
10.Преобразователь частоты содержит один рабочий блок и один блок в нагруженном резерве. Ремонт производится одной бригадой, обеспечивающей среднее время восстановления 0,5 ч. Определить предельно допустимую интенсивность отказов преобразователя, чтобы удовлетворялось условие  .
.
11. Дальномер содержит рабочий блок (Т = 200 ч) и блок в облегченном резерве (Т0=800 ч). Требуется определить допустимую величину среднего времени ремонта θ при условии, что имеется одна ремонтная бригада и должно быть 
Лабораторная работа 5
НАДЕЖНОСТЬ ПРГРАММНОГО ОБЕСПЕЧЕНИЯ
Цель работы
Моделирование параметров надежности программного обеспечения.
Задание к работе
Получите зависимости вероятности безотказной работы и среднего времени наработки до отказа программного обеспечения (ПО) от заданной структуры, от интенсивности и продолжительности его использования,  и
и  соответственно, вероятности проявления ошибки
соответственно, вероятности проявления ошибки  и достигнутого уровня отладки
и достигнутого уровня отладки  (характеристики нескольких исследуемых программ приведены в табл.1).
(характеристики нескольких исследуемых программ приведены в табл.1).
Краткие теоретические сведения
Алгоритм оценки надежности ПО на стадии промышленной эксплуатации включает несколько этапов /З/.
 .Построение графа блок-схемы программы и определение его вероятностных и объемных характеристик производятся по листингам программ.
.Построение графа блок-схемы программы и определение его вероятностных и объемных характеристик производятся по листингам программ.
При определении объема каждого блока учитываются: константы, форматы, используемые в данном блоке команды, собственные подпрограммы. Подпрограммы общего назначения считаются абсолютно надежными. Если какая-либо константа используется в нескольких блоках, она учитывается в одном блоке, общем для всех путей. Вероятности переходов на графе определяются в результате анализа входных и выходных данных каждого блока и условий переходов.
Примечание. В задании приводятся блок-схемы программ различного назначения.
2. Составление перечня возможных путей на графе (рис.  -8) и вычисление объемных характеристик и вероятностей выполнения каждого пути: векторов
-8) и вычисление объемных характеристик и вероятностей выполнения каждого пути: векторов  и
и 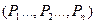 по формулам
по формулам
той 
где 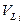 - объем
- объем  й вершины
й вершины  -го пути, Кбайт;
-го пути, Кбайт;  количество вершин в
количество вершин в 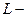 м пути.
м пути.

где  вероятность перехода в
вероятность перехода в  тую вершину
тую вершину 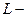 го пути (указана на рис.
го пути (указана на рис.  -8).
-8).
Результаты вычислений целесообразно представить в табличной форме (табл.2.).
Таблица I
Параметры программ
| № Наименование вар. программы | Частота использования И | Достигнутый уров. отладки q | Время использования программ т,г | Кол-во ошибки в ПО на I Кбайт к, | Вероятность проявления ошибки Ро | № рисунка с графом блок-схемы |
| 1,9 Расчет оптимального режима работы | 3 раза в сутки | 0,005 | 1год | 0,0005 | ||
| установки 2,10 Сбор, контроль и обработка | 10 раз в час | 0,005 | 2 года | 0,7 | 0,003 | |
| измерительной информации | ||||||
| 3,11 Оперативное планирование | 1 раз в неделю | 0,001 | 0,5 года | 0,001 | ||
| 4,12 Имитационная модель технологического объекта | 1 раз в сутки | 0,05 | 2 года | 0,5 | 0,007 | |
| 5,13 Имитационная модель процесса функционирования аппаратуры | 2 раза в неделю | 0,001 | 3 года | 0,001 | ||
| 6,14 Вычисление метрологических характеристик измерительных каналов | 2 раза в месяц | 0,025 | 1год | 0,5 | 0,005 | |
| 7,15Моделирование реакции полупроводникового прибора на тепловое воздействие 8,16 Программное обеспечение локальной системы автоматического управления | 3 раза в неделю 10 раз в сутки | 0,01 0,007 | 2 года 1год | 0,6 | 0,005 0,0005 |
Таблица 2
Характеристики путей на графе
| Перечень вершин |  Кбайт Кбайт
| 
| |
Правильность вычислений характеристик пути можно проверить по условию

где 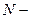 количество путей.
количество путей.

Рис.  . Граф программы расчета оптимального режима работы установки
. Граф программы расчета оптимального режима работы установки
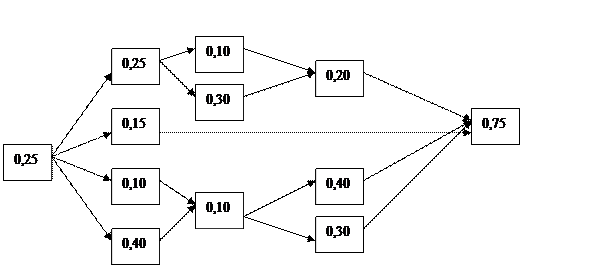

Рис.2. Граф программы сбора, контроля и обработки информации

Рис.3 Граф программы оперативного планирования
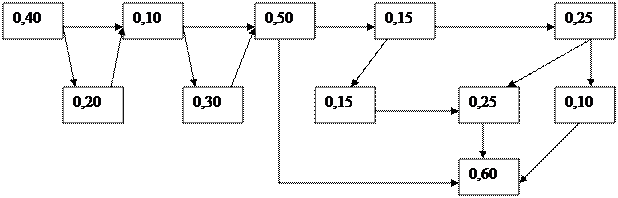
Рис.4 Граф имитационной модели технологического объекта управления

Рис.5 Граф имитационной модели процесса функционирования аппаратуры

Рис.6 Граф программы для вычисления метрологических характеристик измерительных каналов 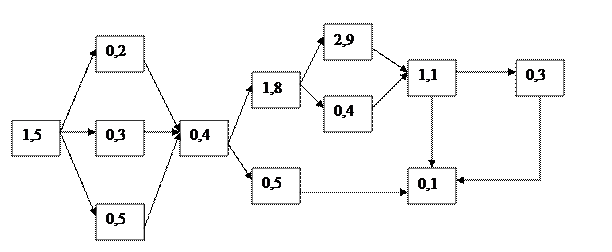
Рис. 7. Граф программного обеспечения локальной системы автоматического управления

Рис. 8. Граф программы моделирования реакции полупроводникового прибора на тепловое воздействие
Выбор значений  (требуемого уровня отладки- снижения количества ошибок в течение опытной эксплуатации) и
(требуемого уровня отладки- снижения количества ошибок в течение опытной эксплуатации) и  (периода времени, за который определяется вероятность безотказной работы) производится в соответствии с /4/.
(периода времени, за который определяется вероятность безотказной работы) производится в соответствии с /4/.
Вероятность проявления ошибки ПО  на стадии опытной эксплуатации рекомендуется выбирать в пределах от 0,I до 0,8, а на стадии промышленной эксплуатации – в пределах от 0,00I до 0,2 в зависимости от значения
на стадии опытной эксплуатации рекомендуется выбирать в пределах от 0,I до 0,8, а на стадии промышленной эксплуатации – в пределах от 0,00I до 0,2 в зависимости от значения  : чем меньше
: чем меньше  , тем меньше
, тем меньше  .
.
Примечание. В задании (см.табл.I) приводятся значения  .
.
4. определение интенсивности использования программного обеспечения (см.табл.I.)
в единицах [  ]=ч-1.
]=ч-1.
5. вычисление показателей надежности программного обеспечения на стадии промышленной эксплуатации:
-вероятности безотказной работы в течение времени
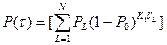 qµτ, (I)
qµτ, (I)
-средней наработки на отказ
 (2)
(2)
При малых значениях  и
и  (
( <0,0I,
<0,0I,  <0,005) и небольших значениях
<0,005) и небольших значениях  можно использовать приближенные формулы для вычисления
можно использовать приближенные формулы для вычисления  и
и  :
:
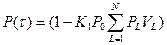 qµτ
qµτ  (3)
(3)
 (4)
(4)
выражения (I)-(4) - используйте для моделирования  и
и  в функции
в функции  изменяя эти параметры в пределах:
изменяя эти параметры в пределах:
0,0005 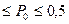 , 0,000I
, 0,000I  0,I; значения
0,I; значения  увеличивайте в диапазоне уменьшения
увеличивайте в диапазоне уменьшения  до 0,4. при варьировании одного из указанных параметров остальные полагайте неизменными и равными заданным.
до 0,4. при варьировании одного из указанных параметров остальные полагайте неизменными и равными заданным.
Контрольные вопросы
1. Сформулируйте понятия надежности ПО.
2. Охарактеризуйте отказ ПО и укажите его причины.
3. Опишите методы прогнозирования надежности ПО на ранних этапах его разработки.
- Опишите модели для оценки надежности ПО в ходе его отладки и эксплуатации.
5. Перечислите способы повышения надежности ПО.
6. Охарактеризуйте методы тестирования ПО.
Задачи
1. Оценить ожидаемое количество ошибок в управляющей программе, в которой содержится 20 ветвлений, 15 связей с прикладными программами, 10 связей с системными программами, 5 операций ввода-вывода, 40 комментариев.
2. Оценить среднее время наработки до отказа программы настройки, содержащей 30 ветвлений, 30 связей с системными программами, 20 операторов обработки данных, 60 комментариев, если среднее время прохождения программы 30 минут, вероятность проявления ошибки при однократном прохождении программы  .
.
3. В ходе отладки программы зафиксированы 3 отказа и соответствующие интервалы времени 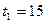 мин,
мин,  мин,
мин,  мин между отказами. Пренебрегая продолжительностью устранения ошибок, оценить среднее значение интервала времени до 4-го отказа.
мин между отказами. Пренебрегая продолжительностью устранения ошибок, оценить среднее значение интервала времени до 4-го отказа.
4. Для повышения надежности программного обеспечения применено модифицированное дуальное программирование. Вероятность отказа основной программы  , а его погрешность
, а его погрешность 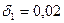 . Оценить параметры
. Оценить параметры  и
и  резервирующей программы, если требуется, чтобы показатели качества работы системы из двух программ составляли
резервирующей программы, если требуется, чтобы показатели качества работы системы из двух программ составляли  а
а  .
.
5. Определить требуемое количество тестов (прохождений программы со случайными исходными данными), которые необходимо провести с положительными исходами (отсутствием отказов), чтобы нижняя доверительная граница вероятности безотказной работы программы составила 0,99, если доверительная вероятность  .
.
Примечание. При решении задач можно использовать данные приложения 5, а также /5,7/.
Лабораторная работа 6
ИСПЫТАНИЯ НА НАДЕЖНОСТЬ
Цель работы
Моделирование законов распределения результатов измерения времени наработки до отказа и определение границ доверительных интервалов. Выполнение этой лабораторной работы прививает навыки обработки результатов экспериментального исследования надежности.
Задание к работе
Промоделируйте заданный закон распределения наработки до отказа с параметрами, указанными в таблице; изобразите его. Определите границы доверительного интервала для среднего времени наработки до отказа (значение доверительной вероятности приведено в таблице).






