Кинематическим способом
Линия влияния силового фактора (опорной реакции или внутреннего усилия) – это графическое изображение закона его изменения в зависимости от координаты точки приложения подвижной единичной сосредоточенной нагрузки.

Рис. 1.29
Для удобства сравнения результатов, вычисленных по линиям влияния и аналитическим способом, оставим принятую ранее нумерацию сечений расчетной схемы многопролетной балки без изменений, как показано на рис. 1.29. При этом указанные в задании сечения A и B совпадают соответственно с сечениями 1 и 3, которые договоримся использовать для дальнейших вычислений.
Порядок построения линии влияния силового фактора в заданном сечении
а) В расчетной схеме необходимо отбросить связь в направлении искомого силового фактора в заданном сечении. Таким образом, получаем геометрически изменяемую систему с одной степенью свободы.
б) В направлении отброшенной связи прикладывается единичная сосредоточенная нагрузка.
в) В точке приложения единичной нагрузки задаемся единичным перемещением и строим схему возможных перемещений для всей балки.
В связи с отсутствием нагрузок, действующих вдоль оси балки, пренебрегаем горизонтальными перемещениями узлов балки и опорных связей.
Определение значения силового фактора по линии влияния
Значение искомого силового фактора Z определяют методом загружения соответствующей линии влияния по формуле:
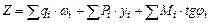 , (1.1)
, (1.1)
где 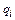 ,
, 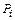 ,
, 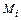 – заданные нагрузки;
– заданные нагрузки; 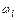 – площадь линии влияния на участке действия распределенной нагрузки
– площадь линии влияния на участке действия распределенной нагрузки 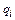 ;
; 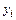 – ордината под сосредоточенной силой
– ордината под сосредоточенной силой 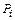 на соответствующей линии влияния;
на соответствующей линии влияния; 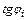 – тангенс угла наклона линии влияния под внешним изгибающим моментом
– тангенс угла наклона линии влияния под внешним изгибающим моментом 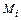 .
.
Правило знаков:
· Знак произведения 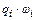 – положительный, если распределенная нагрузка
– положительный, если распределенная нагрузка 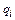 направлена в сторону, противоположную расположению соответствующего участка на линии влияния относительно оси расчетной схемы.
направлена в сторону, противоположную расположению соответствующего участка на линии влияния относительно оси расчетной схемы.
· Знак произведения 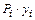 – положительный, если сосредоточенная сила
– положительный, если сосредоточенная сила 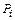 направлена в сторону, противоположную расположению ординаты под данной силой на линии влияния относительно оси расчетной схемы.
направлена в сторону, противоположную расположению ординаты под данной силой на линии влияния относительно оси расчетной схемы.
· Знак произведения 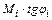 – положительный, если направление изгибающего момента
– положительный, если направление изгибающего момента 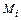 является противоположным повороту участка балки под этим моментом на линии влияния относительно оси расчетной схемы.
является противоположным повороту участка балки под этим моментом на линии влияния относительно оси расчетной схемы.
5.1. Линии влияния вертикальных опорных реакций.
Алгоритм построения линии влияния вертикальной опорной реакции:
а) В заданной расчетной схеме необходимо отбросить вертикальную связь в
направлении искомой опорной реакции.
б) В направлении отброшенной связи прикладывается единичная сосредоточенная сила, направленная вдоль положительного направления оси Y (вверх).
в) В точке приложения единичной силы задаемся единичным перемещением и строим схему возможных перемещений по очереди для каждого диска балки.
5.1.1. Построение линии влияния и определение по ней значения опорной
реакции  (
( ) в сечении 1( A ).
) в сечении 1( A ).
В результате отбрасывания вертикальной связи в т. 1 вместо двухстержневой связи остается одностержневая, воспринимающая горизонтальные перемещения, но разрешающая вертикальные перемещения и поворот относительно этой точки диска 1–2. Прикладывание единичной силы 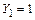 в т. 1 приводит к вертикальному перемещению в направлении действия силы этой точки диска 1–2 на величину, равную 1 (рис. 1.30). Таким образом, на линии влияния опорной реакции
в т. 1 приводит к вертикальному перемещению в направлении действия силы этой точки диска 1–2 на величину, равную 1 (рис. 1.30). Таким образом, на линии влияния опорной реакции  в т. 1 отложим вверх ординату, равную единице (рис. 1.31).
в т. 1 отложим вверх ординату, равную единице (рис. 1.31).
Для того чтобы узнать, как поведет себя т. 2 балки рассмотрим диск 2–5, имеющий на одном конце (т. 2) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 3 и 4 на одностержневые приставные вертикальные связи. Как известно, одностержневая приставная вертикальная связь воспринимает вертикальные перемещения диска в точке расположения опорной связи, но разрешает поворот диска относительно этой точки, поэтому диск 2–5 должен одновременно пройти через т. 3 и 4, что возможно только в одном случае, когда он не меняет своего положения. Значит, диск 2–5 останется на своем месте.
Следовательно, диск 1–2 повернется в шарнире по моменту (т. 2), который разрешает поворот относительно этой точки любого из двух соединенных им дисков, вследствие того, что т. 1 уже изменила свое первоначальное положение, а т. 2 осталась на прежнем месте.
Оставшиеся диск 5–6 и диск 6–7 также не изменят своего положения.

Рис. 1.30
Линия влияния имеет ненулевой участок лишь в пределах сосредоточенной силы, приложенной в т. 8 и равной 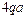 . Поэтому в соответствии с формулой
. Поэтому в соответствии с формулой
(1.1) необходимо вычислить ординату на линии влияния в этой точке (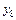 ).
).
Из курса геометрии известно что, в подобных треугольниках сходственные стороны пропорциональны. Следовательно,
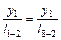 или
или 
 ,
,
где  и
и 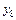 – ординаты на линии влияния соответственно в т. 1 и 8;
– ординаты на линии влияния соответственно в т. 1 и 8;
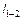 – длина диска 1–2;
– длина диска 1–2;  – длина диска 8–2.
– длина диска 8–2.
Подставляя полученные данные (рис. 1.31) в формулу (1.1), получим:
 ,
,
· произведение 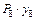 взято с положительным знаком, так как сосредоточенная сила
взято с положительным знаком, так как сосредоточенная сила 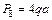 , приложенная в т. 8, направлена вниз, а ордината
, приложенная в т. 8, направлена вниз, а ордината 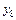 под этой силой на линии влияния расположена в верхней части.
под этой силой на линии влияния расположена в верхней части.

Рис. 1.31
5.1.2. Построение линии влияния и определение по ней значения опорной
реакции  (
( ) в сечении 3( B ).
) в сечении 3( B ).
Прикладывание единичной силы  в т. 3 приводит к вертикальному перемещению в направлении действия силы этой точки диска 2–5 на величину, равную 1 (рис. 1.32). Таким образом, на линии влияния опорной реакции
в т. 3 приводит к вертикальному перемещению в направлении действия силы этой точки диска 2–5 на величину, равную 1 (рис. 1.32). Таким образом, на линии влияния опорной реакции  в т. 3 отложим вверх ординату, равную единице (рис. 1.33).
в т. 3 отложим вверх ординату, равную единице (рис. 1.33).
Рассмотрим диск 2–5, имеющий на одном конце (т. 2) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 4 на одностержневую приставную вертикальную связью. Как известно, одностержневая приставная вертикальная связь воспринимает вертикальные перемещения диска в точке расположения опорной связи, но разрешает поворот диска относительно этой точки, поэтому диск должен пройти через т. 4, а, зная ординату в т. 3, можно без труда построить перемещение диска 2–5 по двум точкам. Таким образом, т. 2 диска 2–5 окажется в верхней части линии влияния, а
т. 5 – в нижней части.
Рассмотрим диск 1–2, имеющий на одном конце (т. 1) шарнирно-неподвижную опору, разрешающую только поворот диска относительно этой точки, а на другом (т. 2) соединяющийся с диском 2–5 при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 1–2 повернется относительно т. 1 вследствие того, что т. 2 уже изменила свое первоначальное положение. Соединив т. 1 с уже построенной для диска 2–5 ординатой в
т. 2, получим перемещение диска 1–2.
Диск 6–7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи.
Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов
соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся с
диском 6–7 при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 5–6 переместится параллельно диску 2–5*, т. е. т. 5 диска 5–6 будет располагаться в верхней части линии влияния, а т. 6 останется на прежнем месте (диск повернется в шарнире).

Рис. 1.32
Линия влияния имеет ненулевые участки в пределах сосредоточенной силы 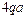 , приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента
, приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента  , приложенного в т. 9.
, приложенного в т. 9.
В соответствии с формулой (1.1) необходимо вычислить:
1) ординаты на линии влияния по концам приложения распределенной нагрузки q (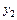 и
и  ), и затем площадь на участке 2–13 между этими ординатами (
), и затем площадь на участке 2–13 между этими ординатами ( );
);
2) ординату на линии влияния в точке приложения сосредоточенной силы 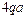 (
(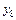 );
);
3) тангенс угла наклона к оси балки линии влияния под изгибающим моментом  (
(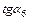 ).
).
1) Зная ординату 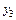 на линии влияния в т. 3 и расстояние
на линии влияния в т. 3 и расстояние 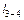 между т. 3 и 4 можно найти
между т. 3 и 4 можно найти 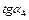 , как отношение противолежащей стороны прямоугольного треугольника к прилежащей, т. е.
, как отношение противолежащей стороны прямоугольного треугольника к прилежащей, т. е. 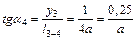 .
.
Зная 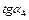 и длины участков
и длины участков  и
и  можно найти ординаты в т. 2 и 13:
можно найти ординаты в т. 2 и 13:
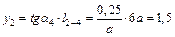 ;
;  .
.
На участке 2–13 линии влияния между ординатами 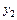 и
и  имеем трапецию, площадь которой находится как произведение полусуммы оснований на высоту, т. е.
имеем трапецию, площадь которой находится как произведение полусуммы оснований на высоту, т. е.
 .
.
2) Из подобия треугольников следует, что
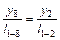 или
или 
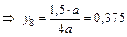 ,
,
где 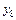 и
и 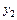 – ординаты на линии влияния соответственно в т. 8 и 2;
– ординаты на линии влияния соответственно в т. 8 и 2;
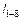 – длина диска 1–8;
– длина диска 1–8; 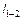 – длина диска 1–2.
– длина диска 1–2.
3) Диски 2–5 и 5–6 после перемещения останутся параллельными друг другу, поэтому 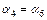 (соответственные углы при параллельных прямых), а значит
(соответственные углы при параллельных прямых), а значит  .
.
Подставляя полученные данные (рис. 1.33) в формулу (1.1), получим:
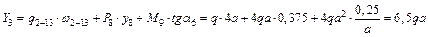 ,
,
· произведение 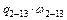 взято с положительным знаком, так как распределенная нагрузка
взято с положительным знаком, так как распределенная нагрузка 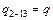 , приложенная на участке 2–13, направлена вниз, а соответствующий ей участок площадью
, приложенная на участке 2–13, направлена вниз, а соответствующий ей участок площадью  на линии влияния расположен в верхней части;
на линии влияния расположен в верхней части;
· произведение 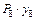 взято с положительным знаком, так как сосредоточенная сила
взято с положительным знаком, так как сосредоточенная сила 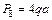 , приложенная в т. 8, направлена вниз, а ордината
, приложенная в т. 8, направлена вниз, а ордината 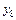 под этой силой на линии влияния расположена в верхней части;
под этой силой на линии влияния расположена в верхней части;
· произведение 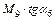 взято с положительным знаком, так как внешний изгибающий момент
взято с положительным знаком, так как внешний изгибающий момент 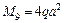 , приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.
, приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.

Рис. 1.33
5.2. Линии влияния усилий – изгибающих моментов в заданном сечении.
Алгоритм построения линии влияния внутреннего изгибающего момента:
а) В расчетной схеме необходимо врезать шарнир по моменту в заданном сечении, в результате чего диск, которому принадлежит это сечение, разделяется на два диска.
б) На каждый из двух полученных дисков в заданном сечении прикладываем по единичному моменту.
в) Сумму углов, образованных в результате поворота полученных дисков относительно оси балки под действием единичных моментов, приравниваем единице и строим схему возможных перемещений по очереди для каждого диска балки.
5.2.1. Построение линии влияния и определение по ней значения изгибающего момента 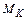 в сечении K.
в сечении K.
В сечении K прикладываем на диск 2– K единичный момент против часовой стрелки, а на диск K– 5 – по часовой стрелке (рис. 1.34). В результате этого врезанный шарнир по моменту в сечении K должен переместиться вверх, но при условии, что оба диска 2– K и K– 5 могут одновременно повернуться в шарнире.
Для начала рассмотрим диск 2– K, имеющий по концам (т. 2 и K) шарниры по моменту и опирающийся по длине в т. 3 на одностержневую приставную вертикальную связь, разрешающую поворот диска относительно этой точки. Предположим, что в т. K диск 2– K переместится вверх под действием единичного момента, при этом он должен пройти через т. 3. Отсюда по двум точкам можно построить перемещение диска 2– K. В этом случае т. 2 диска 2– K окажется в нижней части линии влияния.
Теперь рассмотрим диск K– 5, имеющий на одном конце (т. K) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 4 на одностержневую приставную вертикальную связь,
разрешающую поворот диска относительно этой точки. Предположим, что в т. K диск K– 5 переместится вверх под действием единичного момента, при этом он должен пройти через т. 4. Отсюда по двум точкам можно построить перемещение диска K– 5. Таким образом, т. 5 диска K– 5 переместится вниз.
Так как оба диска 2– K и K– 5 могут одновременно повернуться (изменить свое первоначальное положение), то врезанный шарнир по моменту в сечении K действительно переместится вверх, а диски 2– K и K– 5 займут положения, описанные выше.
Рассмотрим диск 1–2, имеющий на одном конце (т. 1) шарнирно-неподвижную опору, разрешающую поворот диска относительно этой точки, а на другом (т. 2) соединяющийся с диском 2– K при помощи шарнира по моменту,
который разрешает поворот относительно этой точки любого из двух дисков.
Диск 1–2 повернется относительно т. 1 вследствие того, что т. 2 уже изменила свое первоначальное положение. Соединив т. 1 с уже отложенной для диска 2– K ординатой в т. 2, построим перемещение диска 1–2.
Диск 6–7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи.
Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов
соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся с
диском 6–7 при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 5–6 должен переместиться параллельно диску K –5 (см. * на стр. 24), т. е. т. 5 диска 5–6 будет располагаться в верхней части линии влияния, а т. 6 останется на прежнем месте (диск повернется в шарнире).
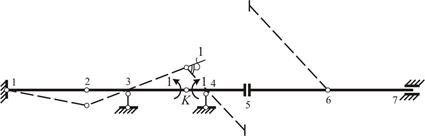
Рис. 1.34
Линия влияния имеет ненулевые участки в пределах сосредоточенной силы 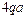 , приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента
, приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента  , приложенного в т. 9.
, приложенного в т. 9.
В соответствии с формулой (1.1) необходимо вычислить:
1) ординаты на линии влияния по концам приложения распределенной нагрузки q (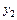 и
и  ), и затем площадь на участке 2–13 между этими ординатами (
), и затем площадь на участке 2–13 между этими ординатами ( );
);
2) ординату на линии влияния в точке приложения сосредоточенной силы 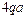 (
(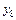 );
);
3) тангенс угла наклона к оси балки линии влияния под изгибающим моментом  (
(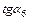 ).
).
1) В соответствии с п. 5.2в: 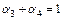 .
.
Пусть 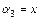 , тогда
, тогда 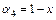 . Зная расстояния
. Зная расстояния  между т. 3 и K и
между т. 3 и K и 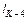 между т. K и 4, а также, принимая
между т. K и 4, а также, принимая 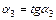 и
и  **, найдем ординату
**, найдем ординату 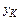 на линии влияния в т. K, как произведение тангенса угла наклона на прилежащую сторону прямоугольного треугольника, т. е.
на линии влияния в т. K, как произведение тангенса угла наклона на прилежащую сторону прямоугольного треугольника, т. е.
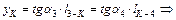
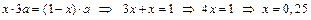 .
.
Таким образом,  ;
;  .
.
Зная  и длины участков
и длины участков  и
и  можно найти ординаты в т. 2 и 13:
можно найти ординаты в т. 2 и 13:
 ;
;  .
.
На участке 2–13 между ординатами 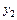 и
и  имеем два треугольника (один треугольник расположен в нижней части на участке 2–3, а другой – в верхней части на участке 3–13), площадь каждого из них находится как половина произведения основания на высоту, т. е.
имеем два треугольника (один треугольник расположен в нижней части на участке 2–3, а другой – в верхней части на участке 3–13), площадь каждого из них находится как половина произведения основания на высоту, т. е.
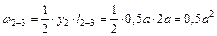 ;
;  .
.
2) Из подобия треугольников следует, что
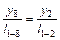 или
или 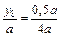
 ,
,
где 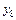 и
и 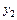 – ординаты на линии влияния соответственно в т. 8 и 2;
– ординаты на линии влияния соответственно в т. 8 и 2;
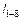 – длина диска 1–8;
– длина диска 1–8; 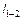 – длина диска 1–2.
– длина диска 1–2.
3) Диски K– 5 и 5–6 после перемещения останутся параллельными друг другу, поэтому 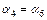 (соответственные углы при параллельных прямых), а значит
(соответственные углы при параллельных прямых), а значит 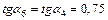 .
.
Подставляя полученные данные (рис. 1.35) в формулу (1.1), получим:

· произведение  взято с отрицательным знаком, так как распределенная нагрузка
взято с отрицательным знаком, так как распределенная нагрузка 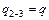 , приложенная на участке 2–3, направлена вниз, а соответствующий ей участок площадью
, приложенная на участке 2–3, направлена вниз, а соответствующий ей участок площадью 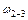 на линии влияния расположен в нижней части;
на линии влияния расположен в нижней части;
· произведение  взято с положительным знаком, так как распределенная нагрузка
взято с положительным знаком, так как распределенная нагрузка 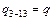 , приложенная на участке 3–13, направлена вниз, а соответствующий ей участок площадью
, приложенная на участке 3–13, направлена вниз, а соответствующий ей участок площадью 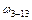 на линии влияния расположен в верхней части;
на линии влияния расположен в верхней части;
· произведение 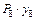 взято с отрицательным знаком, так как сосредоточенная сила
взято с отрицательным знаком, так как сосредоточенная сила 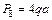 , приложенная в т. 8, направлена вниз, а ордината
, приложенная в т. 8, направлена вниз, а ордината 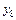 под этой силой на линии влияния расположена в нижней части;
под этой силой на линии влияния расположена в нижней части;
· произведение 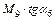 взято с положительным знаком, так как внешний изгибающий момент
взято с положительным знаком, так как внешний изгибающий момент 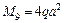 , приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.
, приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.
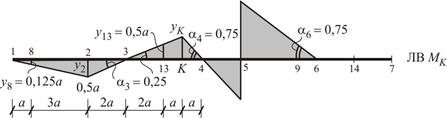
Рис. 1.35
5.2.2. Построение линии влияния и определение по ней значения изгибающего момента  в сечении S.
в сечении S.
Итак, в сечении S прикладываем на диск 6– S единичный момент против часовой стрелки, а на диск S– 7 – по часовой стрелке (рис. 1.36).
Диск S– 7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи. Следовательно, врезанный шарнир в сечении S останется на месте.
Рассмотрим диск 6– S, имеющий по концам (т. 6 и S) шарниры по моменту. Под действием единичного момента, направленного против часовой стрелки, т. 6 диска 6– S переместится вниз. Таким образом, диск 6– S повернется в шарнире
(т. S).
Рассмотрим диск 2–5, имеющий на одном конце (т. 2) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 3 и 4 на одностержневые приставные вертикальные связи. Как известно, одностержневая приставная вертикальная связь воспринимает вертикальные перемещения диска в точке расположения опорной связи, но разрешает поворот диска относительно этой точки, поэтому диск 2–5 должен одновременно пройти через т. 3 и 4, что возможно только в одном случае, когда он не меняет своего положения. Значит, диск 2–5 останется на своем месте.
Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся с диском
6– S при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 5–6 должен переместиться параллельно диску 2–5 (см. * на стр. 24). Следовательно, при условии, что диск 5–6 в т. 5 может перемещаться только в вертикальном направлении, и т. 6 переместилась вниз, данный диск сместится вниз параллельно своему первоначальному положению.
Диск 1–2 также как диск 2–5 не изменит своего положения.

Рис. 1.36
Линия влияния имеет ненулевые участки в пределах изгибающего момента  , приложенного в т. 9 и сосредоточенной силы
, приложенного в т. 9 и сосредоточенной силы 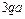 , приложенной в т. 14.
, приложенной в т. 14.
В соответствии с формулой (1.1) необходимо вычислить:
1) ординату на линии влияния в точке приложения сосредоточенной силы 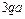 (
(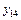 );
);
2) тангенс угла наклона к оси балки линии влияния под изгибающим моментом  (
(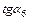 ).
).
1) В соответствии с п. 5.2в: 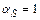 , так как из двух дисков 6– S и S– 7 повернулся лишь первый, а второй не изменил своего положения.
, так как из двух дисков 6– S и S– 7 повернулся лишь первый, а второй не изменил своего положения.
Зная расстояние 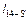 между т. 14 и S, а также, принимая
между т. 14 и S, а также, принимая  (см. ** на стр. 27), найдем ординату
(см. ** на стр. 27), найдем ординату 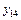 на линии влияния в т. 14, как произведение тангенса угла наклона на прилежащую сторону прямоугольного треугольника, т. е.
на линии влияния в т. 14, как произведение тангенса угла наклона на прилежащую сторону прямоугольного треугольника, т. е.
 .
.
2) Так как участок 5–6 на линии влияния под изгибающим моментом  параллелен оси балки, то
параллелен оси балки, то 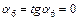 . Поэтому при определении значения изгибающего момента
. Поэтому при определении значения изгибающего момента  в сечении S произведение
в сечении S произведение 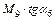 учитывать не будем, поскольку оно равно нулю.
учитывать не будем, поскольку оно равно нулю.
Подставляя полученные данные (рис. 1.37) в формулу (1.1), получим:
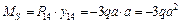 ,
,
· произведение 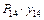 взято с отрицательным знаком, так как сосредоточенная сила
взято с отрицательным знаком, так как сосредоточенная сила  , приложенная в т. 10, направлена вниз, а ордината
, приложенная в т. 10, направлена вниз, а ордината 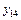 под этой силой на линии влияния расположена в нижней части.
под этой силой на линии влияния расположена в нижней части.
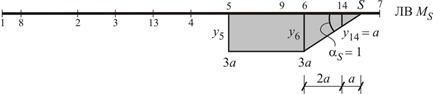
Рис. 1.37
5.3. Линии влияния усилий – поперечных сил в заданном сечении.
Алгоритм построения линии влияния поперечной силы:
а) В расчетной схеме необходимо врезать шарнир по поперечной силе (ползун) в заданном сечении, в результате чего диск, которому принадлежит это сечение, разделяется на два диска.
б) На каждый из двух полученных дисков в заданном сечении прикладываем по вертикальной единичной силе.
в) В заданном сечении расстояние между крайними точками полученных дисков после их возможных перемещений под действием единичных сил приравниваем единице и строим схему возможных перемещений по очереди для каждого диска балки.
5.3.1. Построение линии влияния и определение по ней значения поперечной силы  в сечении K.
в сечении K.
Итак, в сечении K прикладываем на диск 2– K единичную силу, направленную вниз, а на диск K– 5 единичную силу, направленную вверх (рис. 1.38). В результате этого т. K диска 2– K должна переместиться вниз, а т. K диска K– 5 должна переместиться вверх, но при условии, что диски 2– K и K– 5 могут изменить свое первоначальное положение.
Для начала рассмотрим диск 2– K, имеющий на одном конце (т. 2) шарнир по моменту, а на другом (т. K) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 3 на одностержневую приставную вертикальную связь, разрешающую поворот диска относительно этой точки. Предположим, что в
т. K диск 2– K переместится вниз под действием единичной силы, при этом он должен пройти через т. 3. Отсюда по двум точкам можно построить перемещение диска 2– K. В этом случае т. 2 диска 2– K окажется в верхней части линии влияния.
Рассмотрим диск K– 5, имеющий по концам (т. K и 5) шарниры по поперечной силе (ползуны), а также опирающийся по длине в т. 4 на одностержневую приставную вертикальную связь, разрешающую поворот диска относительно этой точки. Предположим, что в т. K диск K– 5 переместится вверх под действием единичной силы, при этом он должен пройти через т. 4. Отсюда по двум точкам можно построить перемещение диска K– 5. Таким образом, т. 5 диска K– 5 переместится вниз. При этом диски 2– K и K– 5 после перемещения должны остаться параллельными друг другу (см. * на стр. 24).
Поскольку диски 2– K и K– 5 могут повернуться, т. е. изменить свое первоначальное положение, то т. K диска 2– K действительно переместится вниз, а т. K диска K– 5 переместится вверх, а значит, диски 2– K и K– 5 займут положения, описанные выше.
Рассмотрим диск 1–2, имеющий на одном конце (т. 1) шарнирно-неподвижную опору, разрешающую поворот диска относительно этой точки, а на другом (т. 2) соединяющийся с диском 2– K при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 1–2 повернется относительно т. 1 вследствие того, что т. 2 уже изменила свое первоначальное положение. Соединив т. 1 с уже отложенной для диска 2– K ординатой в т. 2, получим перемещение диска 1–2.
Диск 6–7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи.
Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов
соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся с
диском 6–7 при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 5–6 должен переместиться параллельно диску K –5 (см. * на стр. 24), т. е. т. 5 диска 5–6 будет располагаться в верхней части линии влияния, а т. 6 останется на прежнем месте (диск повернется в шарнире).
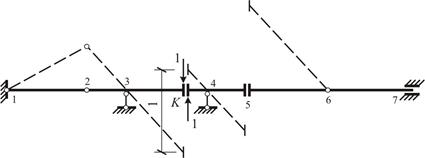
Рис. 1.38
Линия влияния имеет ненулевые участки в пределах сосредоточенной силы 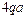 , приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента
, приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента  , приложенного в т. 9.
, приложенного в т. 9.
В соответствии с формулой (1.1) необходимо вычислить:
1) ординаты на линии влияния по концам приложения распределенной нагрузки q (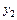 и
и  ), и затем площадь на участке 2–13 между этими ординатами (
), и затем площадь на участке 2–13 между этими ординатами ( );
);
2) ординату на линии влияния в точке приложения сосредоточенной силы 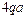 (
(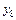 );
);
3) тангенс угла наклона к оси балки линии влияния под изгибающим моментом  (
(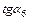 ).
).
1) В соответствии с п. 5.3в:  .
.
Пусть 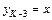 , тогда
, тогда  . Зная расстояния
. Зная расстояния  между т. 3 и K и
между т. 3 и K и 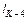 между т. K и 4, для двух подобных прямоугольных треугольников можно записать:
между т. K и 4, для двух подобных прямоугольных треугольников можно записать:
 или
или 
 .
.
Таким образом, 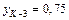 ;
; 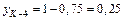 .
.
Зная ординату 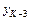 на линии влияния и расстояние
на линии влияния и расстояние  можно найти
можно найти  , как отношение противолежащей стороны прямоугольного треугольника к прилежащей, т. е.
, как отношение противолежащей стороны прямоугольного треугольника к прилежащей, т. е.  .
.
Зная  и длины участков
и длины участков  и
и  можно найти ординаты в т. 2 и 13:
можно найти ординаты в т. 2 и 13:
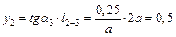 ;
;  .
.
Найдем площадь на участке 2–13 между ординатами 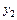 и
и  . На участке
. На участке
2–13 мы имеем два треугольника (один треугольник расположен в верхней части на участке 2–3, а другой – в нижней части на участке 3–13), площадь каждого из них находится как половина произведения основания на высоту, т. е.
 ;
; 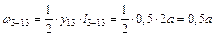 .
.
2) Из подобия треугольников следует, что
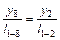 или
или 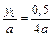
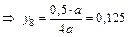 ,
,
где 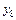 и
и 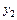 – ординаты на линии влияния соответственно в т. 8 и 2;
– ординаты на линии влияния соответственно в т. 8 и 2;
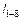 – длина диска 1–8;
– длина диска 1–8; 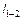 – длина диска 1–2.
– длина диска 1–2.
3) Диски 2– K, K– 5 и 5–6 после перемещения останутся параллельными друг другу, поэтому 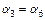 (соответственные углы при параллельных прямых), а значит
(соответственные углы при параллельных прямых), а значит  .
.
Подставляя полученные данные (рис. 1.39) в формулу (1.1), получим:
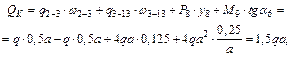
· произведение  взято с положительным знаком, так как распределенная нагрузка
взято с положительным знаком, так как распределенная нагрузка 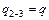 , приложенная на участке 2–3, направлена вниз, а соответствующий ей участок площадью
, приложенная на участке 2–3, направлена вниз, а соответствующий ей участок площадью 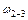 на линии влияния расположен в верхней части;
на линии влияния расположен в верхней части;
· произведение  взято с отрицательным знаком, так как распределенная нагрузка
взято с отрицательным знаком, так как распределенная нагрузка 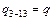 , приложенная на участке 3–13, направлена вниз, а соответствующий ей участок площадью
, приложенная на участке 3–13, направлена вниз, а соответствующий ей участок площадью 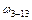 на линии влияния расположен в нижней части;
на линии влияния расположен в нижней части;
· произведение 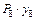 взято с положительным знаком, так как сосредоточенная сила
взято с положительным знаком, так как сосредоточенная сила  , приложенная в т. 8, направлена вниз, а ордината
, приложенная в т. 8, направлена вниз, а ордината 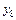 под этой силой на линии влияния расположена в верхней части;
под этой силой на линии влияния расположена в верхней части;
· произведение 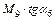 взято с положительным знаком, так как внешний изгибающий момент
взято с положительным знаком, так как внешний изгибающий момент 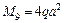 , приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.
, приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.

Рис. 1.39
5.3.2. Построение линии влияния и определение по ней значения поперечной силы  в сечении S.
в сечении S.
Итак, в сечении S прикладываем на диск 6– S единичную силу, направленную вниз, а на диск S– 7 единичную силу, направленную вверх (рис. 1.40).
Диск S– 7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи. Следовательно, врезанный шарнир в сечении S останется на месте.
Рассмотрим диск 6– S, имеющий на одном конце (т. 6) шарнир по моменту,
а на другом (т. S) – шарнир по поперечной силе (ползун). Так как, во-первых,
диск 6– S в т. S может перемещаться только в вертикальном направлении, во-вторых, в т. S на диск 6– S действует единичная сила, направленная вниз, и, наконец, диск 6– S должен переместиться параллельно диску S– 7 (см. * на стр. 24), то следовательно, диск 6– S сместится вниз параллельно своему первоначальному положению.
Рассмотрим диск 2–5, имеющий на одном конце (т. 2) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 3 и 4 на одностержневые приставные вертикальные связи. Как известно, одностержневая приставная вертикальная связь воспринимает вертикальные перемещения диска в точке расположения опорной связи, но разрешает поворот диска относительно этой точки, поэтому диск 2–5 должен одновременно пройти через т. 3 и 4, что возможно только в одном случае, когда он не меняет своего положения. Значит, диск 2–5 останется на своем месте.
Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся при помощи шарнира по моменту с диском 6– S. Диск 5–6 должен переместиться параллельно диску 2–5 (см. * на стр. 24). Следовательно, при условии, что диск 5–6 в т. 5 может перемещаться только в вертикальном направлении, и т. 6 переместилась вниз, диск 5–6 сместится вниз параллельно своему первоначальному положению.
Диск 1–2 также как диск 2–5 не изменит своего положения.

Рис. 1.40
Линия влияния имеет ненулевые участки в пределах изгибающего момента  , приложенного в т. 9 и сосредоточенной силы
, приложенного в т. 9 и сосредоточенной силы 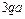 , приложенной в т. 14.
, приложенной в т. 14.
В соответствии с формулой (1.1) необходимо вычислить:
1) ординату на линии влияния в точке приложения сосредоточенной силы 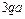 (
(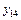 );
);
2) тангенс угла наклона к оси балки линии влияния под изгибающим моментом  (
(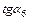 ).
).
1) В соответствии с п. 5.3в:  , так как в сечении S под действием единичных сил из двух дисков 6– S и S– 7 переместился лишь первый.
, так как в сечении S под действием единичных сил из двух дисков 6– S и S– 7 переместился лишь первый.
Так как диски 5–6 и 6– S одновременно переместились параллельно оси балки, следовательно, на участке 5– S будем иметь одинаковую ординату, равную 1. Отсюда 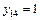 .
.
2) Так как участок 5–6 на линии влияния под изгибающим моментом  параллелен оси балки, то
параллелен оси балки, то 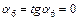 . Поэтому при определении значения поперечной силы
. Поэтому при определении значения поперечной силы  в сечении S произведение
в сечении S произведение 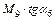 не будем учитывать, поскольку оно равно нулю.
не будем учитывать, поскольку оно равно нулю.
Подставляя полученные данные (рис. 1.41) в формулу (1.1), получим:
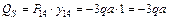 ,
,
· произведение 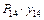 взято с отрицательным знаком, так как сосредоточенная сила
взято с отрицательным знаком, так как сосредоточенная сила  , приложенная в т. 14, направлена вниз, а ордината
, приложенная в т. 14, направлена вниз, а ордината 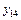 под этой силой на линии влияния расположена в нижней части.
под этой силой на линии влияния расположена в нижней части.

Рис. 1.41
В заключении необходимо отметить, что опорные реакции  ,
,  и внутренние усилия (изгибающие моменты
и внутренние усилия (изгибающие моменты  ,
, 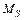 и поперечные силы
и поперечные силы 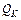 ,
,  ), вычисленные по линиям влияния, соответствуют результатам, полученным ранее аналитическим способом[*].
), вычисленные по линиям влияния, соответствуют результатам, полученным ранее аналитическим способом[*].
* При любых вариантах перемещений дисков, располагающихся по обеим сторонам ползуна, эти диски всегда должны оставаться параллельными друг другу.
** При определении значения силового фактора по линии влияния тангенс малого угла можно принять равным значению самого угла, т. е..
[*] Вычисленный по линии влияния положительный изгибающий момент в заданном сечении соответствует варианту аналитического расчета, когда растянутые волокна поперечного сечения расположены понизу балки (РВ/Н).






