Отметим участки, вдоль которых закон изменения изгибающего момента не меняет своего математического вида. Такими участками являются:
Рис. 1.27
· 1–8 — линейный закон изменения изгибающего момента, что соответствует постоянному значению поперечной силы вдоль этого участка; знак усилия определяется направлением поворота оси участка к линии графика на кратчайший угол (в данном случае знак положительный – поворот оси происходит по часовой стрелке) (рис. 1.27а); значение поперечной силы определяется тангенсом угла наклона прямой графика:
;
· 8–2 — линейный закон изменения изгибающего момента, что соответствует постоянному значению поперечной силы вдоль этого участка; знак усилия отрицательный – поворот оси происходит против часовой стрелки (рис. 1.27а); значение поперечной силы определяется тангенсом угла наклона прямой графика:
;
· 2–11–3 — параболический закон изменения изгибающего момента, что соответствует линейному закону изменения значения поперечной силы; значения ординат усилия в сечениях 2 и 3 определяются на базе разложения эпюры изгибающего момента на треугольник и параболу; знак первой составляющей усилия 
и 
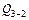отрицательный – поворот оси к пунктиру, соединяющему крайние точки участка, происходит против часовой стрелки; знак второй составляющей усилия – положительный (поворот от пунктира к параболе возле т. 2 происходит по часовой стрелке), а усилия 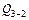– отрицательный (поворот от пунктира к параболе возле т. 3 происходит против часовой стрелки) (рис. 1.27б); значение первой составляющей определяется тангенсом угла наклона пунктира к оси, а второй – равно 
:
;
;
· 3–12–13 — параболический закон изменения изгибающего момента, что соответствует линейному закону изменения значения поперечной силы; значения ординат усилия в сечениях 3 и 13 определяются на базе разложения эпюры изгибающего момента на два треугольника и параболу; знак первой составляющей усилия 
и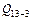 
положительный – поворот оси к пунктиру, соединяющему крайние точки участка, происходит по часовой стрелке; знак второй составляющей усилия – положительный (поворот от пунктира к параболе возле т. 3 происходит по часовой стрелке), а усилия 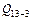– отрицательный (поворот от пунктира к параболе возле т. 13 происходит против часовой стрелки) (рис. 1.27б); значение первой составляющей определяется тангенсом угла наклона пунктира к оси, а второй – равно :
;
;
· 13–4 — линейный закон изменения изгибающего момента, что соответствует постоянному значению поперечной силы вдоль этого участка; знак усилия положительный – поворот оси происходит по часовой стрелке (рис. 1.27а); значение поперечной силы определяется тангенсом угла наклона прямой графика:
;
· 4–9 — линейный закон изменения изгибающего момента, причем линия графика параллельна оси расчетной схемы; тангенс угла наклона прямой графика к оси равен нулю (рис. 1.27а), а следовательно, и значение поперечной силы на этом участке также равно нулю:
;
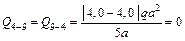· 10–14 — изгибающий момент равен нулю (линия графика совпадает с осью расчетной схемы); тангенс угла наклона прямой графика к оси равен нулю (рис. 1.27а), а следовательно, и значение поперечной силы на этом участке также равно нулю:
;
· 14–7 — линейный закон изменения изгибающего момента, что соответствует постоянному значению поперечной силы вдоль этого участка; знак усилия отрицательный – поворот оси происходит против часовой стрелки (рис. 1.27а); значение поперечной силы определяется тангенсом угла наклона прямой графика:
.
Общая эпюра поперечных сил изображена на рис. 1.28.
Рис. 1.28
