Лабораторна робота № 4
ЛОГІЧНИЙ СИНТЕЗ ТА ДОСЛІДЖЕННЯ СХЕМ АВТОМАТИЗАЦІЇ ТИПОВИХ ПРОМИСЛОВИХ МЕХАНІЗМІВ НА ОСНОВІ ПРОГРАМОВАНИХ ЛОГІЧНИХ ІНТЕГРАЛЬНИХ СХЕМ (ПЛІС)
Тривалість лабораторної роботи – 4 год.
Тривалість домашньої роботи – 4 год.
Мета роботи – навчитися програмувати ПЛІС Altera Cyclone II EP2C5T144C8N для реалізації однотактних та багатотактних схем автоматичного керування промисловими механізмами.
Основні теоретичні відомості
4.1.1 Мінімізація логічних функцій за допомогою карт Карно
Карта Карно – один з графічних способів подання логічних функцій. Для функцій n змінних вона складається з 2n клітинок, причому кожна клітинка відповідає певному набору змінних. Вигляд карт Карно для функцій 2,3 і 4-ти змінних зображений на рис. 4.1. Вхідні змінні розміщуються з зовнішніх сторін карти проти її рядків або стовпців.
Значення вхідної змінної стосується усіх клітинок у рядку або стовпці і дорівнює 1, якщо проти рядка або стовпця є дужка з позначенням цієї змінної. Для решти рядків і стовпців значення змінної дорівнює 0. У клітинках карти записується те значення функції, яке вона має при наборах вхідних змінних, що відповідають цим клітинкам.
Рисунок 4.1 – Форма запису карт Карно
Функцію, задану алгебраїчним виразом, можна подати у вигляді карти Карно. Для цього передусім задану функцію треба подати в диз’юнктивній (ДНФ) або кон’юнктивній (КНФ) нормальній формі. При використанні карт Карно для мінімізації логічних функцій необхідно побудувати карту для відповідної кількості змінних і нанести на неї задану функцію. Потім слід об’єднати сусідні клітинки з одиницями в контури, записати вирази для контурів і скласти їх диз’юнкцію.
4.1.2 Синтез багатоактних схем методом таблиць переходів та карт Карно
Схема називається багатотактною, якщо стан її виходів залежить не тільки від набору вхідних сигналів у даний момент часу, але й від послідовності їх надходження.
Синтез схеми методом таблиць переходів і карт Карно виконується в такій послідовності:
1) складання первинної таблиці переходів;
2) стиснення первинної таблиці переходів;
3) визначення кількості і розміщення станів проміжних змінних;
4) складання карт Карно для проміжних і вихідних змінних і визначення за ними алгебричних виразів.
Складання первинної таблиці переходів. Цей етап починається з визначення кількості вихідних станів схеми. Оскільки умови роботи схеми не передбачають жодних обмежень на послідовність надходження вхідних сигналів, тому слід розглянути усі можливі комбінації вхідних сигналів і для кожної з них визначити кількість можливих станів схеми. Після визначення кількості станів схеми будуємо первинну таблицю переходів.
Стисненням первинної таблиці переходів. Ця операція виконується з метою скорочення кількості рядків таблиці шляхом сполучення кількох рядків в один.
Визначення кількості і розміщення станів проміжних змінних. Кількість проміжних змінних визначається виходячи з того, що кожному рядку стисненої таблиці переходів повинна відповідати своя певна комбінація значень проміжних змінних.
Складання карт Карно для проміжних і вихідних змінних і визначення за ними алгебричних виразів. Карти Карно складають так, щоб вхідні змінні розміщувалися зверху карт так само, як і у середній частині таблиці переходів, а проміжні змінні – ліворуч.
4.1.3 Синтез схем керування на основі циклограм
Циклограма – це графічне зображення послідовності роботи окремих елементів схеми у часі.
Синтез виконують у такій послідовності:
1. Записують умову спрацьовування у вигляді формули 
, до якої входить сигнал, змінювання стану якого визначає початок вмикального такту. В умові спрацьовування він записується в тому стані, в якому перебував у вмикальному такті. Наприклад, для циклограми на рис. 4.2 умова спрацьовування.
Рисунок 4.2. – Циклограма
2. Виконують першу перевірку реалізованості циклограми. При цьому перевіряють, чи зберігається значення 
протягом усього вмикального періоду.
Якщо ця умова виконується, то попередньо записана функція є остаточною і змінюванню не підлягає. Якщо ж функція змінює своє значення протягом вмикального періоду, звичайно застосовується самоблокування і умова спрацьовування записується у вигляді
Для циклограми на рис. 4.2 необхідно ввести самоблокування, тому що сигнал 
змінює свій стан протягом вмикального періоду.
3. Записують умову неспрацьовування у вигляді формули 
. До цієї умови входить сигнал, що змінює свій стан на початку вимикального такту. Сигнал цього елементу записують у вигляді інверсії того стану, в якому він перебуває у вимикальному такті. Для циклограми на рис 4.2 умова неспрацьовування
.
4. Виконують другу перевірку реалізованості циклограми. Перевіряють, чи зберігається значення 
протягом усього вмикального періоду. Якщо ця умова виконується, то записана функція 
є остаточною. Якщо ж функція змінює своє значення протягом вмикального періоду, то необхідно ввести проміжний елемент 
, який змінює свій стан протягом періоду вмикання вихідного елемента, але після того, як змінить значення функція , і залишається у цьому стані принаймні до кінця періоду вмикання вихідного елемента.
Умову неспрацьовування у разі введення проміжного елемента записують у вигляді інверсії кон’юнкції двох сигналів 
і 
, тобто 
. Стани сигналів і беруть такими, які вони є у вимикальному такті.
Для циклограми на рис.4.2 друга перевірка не задовольняється, тому введено проміжну змінну , лінію дії якої показано на рисунку. Після введення проміжної змінної умова неспрацьовування матиме вигляд:
.
5. Записують попередню формулу вмикання елемента у вигляді кон’юнкції умов спрацьовування та неспрацьовування, отриманих після виконання першої та другої перевірок. Для циклограми на рис. 4.2
.
6. Виконують третю перевірку реалізованості циклограми. Для цього функцію 
треба подати в диз’юнктивній нормальній формі (ДНФ), розкривши дужки, і перевірити, чи не набуває значення 1 будь-яка елементарна кон’юнкція в одержаній ДНФ протягом вимикального періоду. Якщо таких елементарних кон’юнкцій немає, то третя перевірка задовольняється і логічну формулу для вихідного елемента змінювати не треба. Якщо ж така кон’юнкція є, то це спричинює помилкове спрацьовування вихідного елемента. У цьому разі треба ввести проміжний елемент , який мав би різні значення для комбінації сигналів, що відповідає цій кон’юнкції, у вмикальному і вимикальному періодах.
Сигнал проміжного елемента додається у вигляді кон’юнкції до тієї елементарної кон’юнкції, яка дорівнює одиниці одночасно у вмикальному та вимикальному періодах. Стан цього елемента беруть таким, який він має у вмикальному періоді для комбінації сигналів, що відповідають розглядуваній кон’юнкції.
Для циклограми на рис.4.2
і третя перевірка задовольняється, тому що жодна з комбінацій сигналів (
, 
; , 
; 
, ; , ) не трапляється у вимикальному періоді елемента 
. Тому формула 
є остаточною.
7. Складають формули для всіх проміжних елементів, які були введені під час виконання перевірок реалізованості циклограми. Для них логічні формули складаються за такими ж самими правилами, як і для вихідних.
Для циклограми на рис. 4.2 введено один проміжний елемент . Визначимо для нього логічну формулу.
Умова спрацьовування
,
умова неспрацьовування
.
Перша перевірка: значення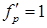 
не зберігається протягом усього вмикального періоду, тому застосовуємо самоблокування і записуємо умову спрацьовування у вигляді:
.
Друга і третя перевірки задовольняються. Остаточна логічна формула для проміжного елемента
4.1.4 Синтез схем автоматики на тригерах
При синтезі схем на тригерах умови роботи багатотактних схем подаються у вигляді графів переходів.
Граф переходів – це графічне зображення послідовності роботи багатотактної схеми. Елементами графа є вершини і ребра. Вершини відповідають станам схеми і позначаються кружками. Ребра – це лінії із стрілками, що з’єднують вершини і показують напрям переходу з одного стану схеми в інший.
Кількість вершин графа при синтезі асинхронних схем на RS – тригерах визначається з умови 2 n³S, де S- кількість станів схеми; 2 n– кількість вершин графа; n – кількість тригерів.
Вершини графа рекомендується розміщувати так, щоб при n= 2 вони створювали конфігурацію 2 х 2, при n= 3– конфігурацію 4 х 2, а при n= 4 - конфігурацію 4 х 4. Вигляд графа переходів при n= 3 показано на рис. 1.3.3.
Рисунок 4.3 – Вигляд графа переходів при n= 3
Вихідні сигнали тригерів виконують роль проміжних змінних, тому тригери та їх вихідні сигнали позначаються буквами Р 1, Р 2, ... Ці позначення записують зверху ліворуч від графа.
Кожна вершина графа кодується набором значень вихідних сигналів тригерів. Коди вибираються так, щоб для сусідніх вершин вони відрізнялися значенням тільки однієї змінної. У вихідному стані схеми (стан очікування) звичайно приймають, що усі проміжні змінні дорівнюють нулеві. Значення проміжних змінних для кожної вершини записуються над кружками у тій черговості, в якій записані позначення тригерів.
Вершини, між якими повинні відбуватися переходи, з’єднують ребрами із стрілками. Над стрілками або праворуч від них, якщо ребра спрямовано вертикально, записують позначення вхідних сигналів, що спричинюють ці переходи.
При побудові схем на асинхронних RS – тригерах переходи можна робити тільки між сусідніми вершинами. Якщо ця умова не виконується, то необхідно передбачити так звані природні переходи (за рахунок подавання вхідного сигналу одиниця) через проміжні нестійкі стани.
Як приклад побудуємо граф переходів, що описує роботу схеми керування механізмом М, який працює в режимі циклів, що повторюються. У вихідному положенні механізму натиснутий кінцевий вимикач SQ1. Цикл роботи починається після надходження команди "Пуск". Механізм переміщується в положення, що фіксується кінцевим вимикачем SQ2, стоїть протягом часу 
, переміщується в положення, що фіксується кінцевим вимикачем SQ3, стоїть протягом часу 
, а потім повертається в вихідне положення. Для повторення циклу необхідно знов подати команду "Пуск". Якщо ця команда надходить безперервно, то після відпрацьовування одного циклу автоматично починається наступний.
Приймемо такі позначення вхідних і вихідних сигналів, а також сигналів таймерів, які необхідно розглядати як вхідні сигнали для графа переходів. Вхідні сигнали: а – команда "Пуск"; b, с, d – сигнали кінцевих вимикачів SQ1, SQ2, SQ3 відповідно; t 1, t 2 – сигнали таймерів, що дають затримки і . Вихідні сигнали: f 1 – команда на переміщення механізму з вихідного положення, f 2 – команда на повернення механізму в вихідне положення.
Побудову графа переходів починаємо з визначення кількості станів, в яких може перебувати схема автоматичного керування. Таких станів шість:1– вихідне положення; 2– переміщення з вихідного положення; 3– стоянка протягом часу ; 4 – подальше переміщення; 5– стоянки протягом часу ; 6 – повернення в вихідне положення.
Виходячи з кількості станів схеми 6<23, визначаємо кількість тригерів n= 3 і кількість вершин графа переходів 23=8. Позначаємо проміжні змінні Р 1, Р 2, Р 3, будуємо 8 вершин графа і кодуємо їх комбінаціями значень проміжних змінних (рис. 4.3).
Кожному станові схеми ставимо у відповідність одну з вершин графа, причому стани, між якими повинен відбуватися перехід згідно з умовами роботи схеми, розміщуємо у сусідніх вершинах. Вільні вершини використовуємо для переходу з стану 6 в стан 2 під час роботи схеми в режимі циклів, що повторюються, або в стан 1 при відпрацьовуванні поодиноких циклів.
Позначення вихідних сигналів f 1 i f 2 записано під позначеннями проміжних змінних. Значення f 1 i f 2 для кожного стану схеми записуємо під відповідними вершинами графа.
Синтез схеми полягає у записі умов вмикання і скидання кожного тригера. Для цього охоплюють замкнутою лінією всі стани на графі переходів, в яких значення вихідного сигналу даного тригера дорівнює одиниці. Вхідні сигнали схеми, позначення яких стоять на ребрах, що заходять в одержану замкнуту область, встановлюють тригер в стан 1, а вхідні сигнали на ребрах, що виходять з цієї області, скидають тригер в стан 0.
Умови вмикання тригера записуються у вигляді добутку сигналу на ребрі, що заходить в область, і сигналів решти тригерів, стан яких не змінюється при переході, позначеному ребром. Наприклад, якщо сигнал на ребрі, що заходить в область з одиничним значенням вихідного сигналу тригера Р 1, дорівнює а, а тригери Р 2 і Р 3 не перемикаються, а зберігають стан Р 2=1, Р 3=0, то умова вмикання тригера Р1 записується у вигляді
.
Якщо в замкнуту область входить кілька ребер, то умова вмикання тригера записується у вигляді суми добутків відповідних сигналів, складених для кожного ребра.
Умова скидання тригера записується аналогічно для кожного ребра, що виходить з даної області, і подається у вигляді формули RPi. Описану процедуру виконують для кожного тригера і визначають для них умови вмикання і скидання.
Застосувавши описану процедуру визначення умов вмикання і скидання тригерів, для графа переходів на рис.23 отримаємо:
; 
;
; 
;
; 
.
Формули для вихідних сигналів f 1i f 2 записуються як комбінаційні функції вихідних сигналів тригерів Р 1, Р 2, Р3. Дійсно, функція f 1=1 в станах 2 і 4, тобто в станах, яким відповідають такі комбінації значень вихідних сигналів тригерів: р 1=0, р 2=0, р 3=1 і р 1=0, р 2=1, р 3=0. Тому
Аналогічно, функція f 2 = 1 в стані 6 (р 1 р 2 р 3 = 111), тобто
f 2 =p 1 p 2 p 3.
Таймер Т 1 вмикається в стані 3 (р 1 р 2 р 3 = 011 ), а таймер Т 2 – в стані 5
(р 1 р 2 р 3 = 110), тому
;
.
Синтез синхронних схем на JК -тригерах виконується аналогічно. Різниця полягає у тому, що для синхронних схем при побудові графа переходів є припустимими переходи між будь-якими вершинами графа, а не обов’язково сусідніми, тобто природні переходи не потрібні. Умови вмикання тригерів записують у вигляді формули Jрі, умови скидання – у вигляді 
.
Програма роботи
Перед початком лабораторної роботи група ділиться на бригади відповідно до кількості робочих місць. Кожному студенту бригади необхідно вибрати один із варіантів (1-6), який містить 4 завдання, з таблиці 4.1. Для кожного з чотирьох завдань необхідно:
1. Виконати логічний синтез схеми керування, та отримати логічні вирази, що описують схему (виконується вдома під час СРС).
2. За виразами у пункті 1 скласти схему на логічних елементах в пакеті програмного забезпечення Quartus II.
3. Зробити позначення виводів вхідних та вихідних змінних.
4. Провести часову симуляцію роботи схеми.
5. Записати програму до ПЛІС.
6. Підключити кнопки, світлодіоди, мікродвигуни і т.п. до входів/виходів ПЛІС відповідно до заданої кількості вхідних/вихідних сигналів, зробити «підтяжку» на GND вхідних сигналів.
7. Перевірити відпрацювання заданих умов роботи на стенді.
8. Показати зібрану схему викладачу та продемонструвати її роботу (викладач підтверджує своїм підписом у протоколі працездатність схеми);
9. Оформити звіт по лабораторній роботі та зробити висновки.
Таблиця 4.1 – Розподіл номерів завдань по варіантах
| Бригада № | № студента в бригаді | Номери завдань |
| 1.1 | 1.1, 2.1, 3.1, 4.1 | |
| 1.2 | 1.2, 2.24, 3.24, 4.2 | |
| 1.3 | 1.3, 2.3, 3.3, 4.3 | |
| 1.4 | 1.4, 2.4, 3.4, 4.4 | |
| 1.5 | 1.5, 2.6, 3.7, 4.8 | |
| 1.6 | 1.6, 2.23, 3.9, 4.10 | |
| 2.1 | 1.21, 2.5, 3.5, 4.5 | |
| 2.2 | 1.6, 2.6, 3.23, 4.6 | |
| 2.3 | 1.22, 2.7, 3.22, 4.7 | |
| 2.4 | 1.8, 2.8, 3.8, 4.8, | |
| 2.5 | 1.9, 2.10, 3.11, 4.12 | |
| 2.6 | 1.24, 2.11, 3.12, 4.13 | |
| 3.1 | 1.9, 2.9, 3.9, 4.9 | |
| 3.2 | 1.10, 2.10, 3.10, 4.10 | |
| 3.3. | 1.11, 2.11, 3.11, 4.20 | |
| 3.4 | 1.12, 2.12, 3.12, 4.17, | |
| 3.5 | 1.13, 2.2, 3.4, 4.5 | |
| 3.6 | 1.14, 2.3, 3.6, 4.7 | |
| 4.1 | 1.13, 2.13, 3.13, 4.19 | |
| 4.2 | 1.14, 2.14, 3.14, 4.14 | |
| 4.3 | 1.15, 2.15, 3.15, 4.15 | |
| 4.4 | 1.23, 2.16, 3.16, 4.16 | |
| 4.5 | 1.10, 2.10, 3.11, 4.11 | |
| 4.6 | 1.5, 2.6, 3.7, 4.18 | |
| 5.1 | 1.17, 2.17, 3.5, 4.8 | |
| 5.2 | 1.5, 2.18, 3.2, 4.19 | |
| 5.3 | 1.8, 2.2, 3.17, 4.17 | |
| 5.4 | 1.4, 2.3, 3.18, 4.22 | |
| 5.5 | 1.18, 2.19, 3.7, 4.8 | |
| 5.6 | 1.6, 2.20, 3.9, 4.23 | |
| 6.1 | 1.7, 2.21, 3.19, 4.21 | |
| 6.2 | 1.19, 2.22, 3.6, 4.20 | |
| 6.3 | 1.7, 2.7, 3.20, 4.7 | |
| 6.4 | 1.20, 2.8, 3.21, 4.24, | |
| 6.5 | 1.9, 2.10, 3.11, 4.12 | |
| 6.6 | 1.10, 2.11, 3.12, 4.13 |
