1 Турлапов А.В. Ферми-газ атомов // Письма в журнал Экспериментальной и Теоретической Физики. - 1995. - T. 95(4). - C.104-112.
2 Chin C., Grimm R., Julienne P., and Tiesinga E.. Fesh bach resonances in ultracold gase // Review of Modern Physics 82. - 2010. - P.1225-1286.
3 Kohler T., Goral K., and Julienne P.S. Production of cold molecules via magnetically tunable Fesh bach resonance // Review of Modern Physics 78. - 2006. - P.1311-1361.
4 Bloch, Dalibard J., and Zwerger W. Many-body physics with ultracold gase // Review of Modern Physics 80. - 2008. - P. 885-964.
5 Yurovsky V.A., Olshanii M., and Weiss D.S. Collisions, correlations, and intagrability in atom wave guide // Advances in Atomic, Molecular, and Optical Physics 55. - 2008. – P. 61-138.
6 Martiyanov K., Makhalov V., and Turlapov A. Observation of a two-dimensional Fermi gas of atom // Physical Review Letters 105. - 2010. - P.030404.
7 Zurn G., Serwane F., Lompe T., Wenz A.N., Ries M.G. Fermionization of two distinguishable fermions // Physical Review Letters 108. - 2012. -P. 075303.
8 Busch T., Englert B.-G., Rzazewski K., and Wilkens M. Two Cold Atoms in a Harmonic Trap // Found. Phys. -1998. - P. 549.
9 Olshanii M. Atomic scattering in the presence of an external confinement and a gass of impenetrable bosons // Physical Review Letters 81. - 2010. - P. 938 - 941.
10 Ni K.K., Ospelkaus S., Wang D., Quemener G., Neyenhuis B., M. H. G. de Miranda, Bohn L. Dipolar Collisions of Polar Molecules in the Quantum Regime // Nature. - 2010. – P. 1324-1328.
11 Турлапов А.В. Экспериментальное исследование ультрахолодного газа ферми-атомов // Автореферат диссертации на соискание ученой степени доктора физико-математических наук - Нижний Новгород. -2012.
12 Hu C.Y.,Melezhik V. // Phys.Rev.Lett. 90. - 2003. - P. 083202.
13 Melezhik V. S. A computational method for quantum dynamics of a three- dimensional atom in strong fields // Аtoms and molecules in strong external fields - Eds.: P. Schmelcher and W. Schweizer- Plenum Press - New-York. -1998. – P. 89-94.
14 Melezhik V. S. Polarization of harmonics generation from a hydrogen atom in a strong laser field // Phys. Lett. - A230.-1997. - P. 203–208.
15 Melezhik V. S. Mathematical modeling and computational science // Lecture Notes in ComputerScience - Volume 7125 - Springer-Verlag - Berlin Heidelberg. - 2012. - P. 94–107.
16 Dineykhan M., Efimov G.V., Ganbold G., Nedelko S.N. Oscillator Representation in Quantum Physics // Lecture Notes in Physics. Berlin - Springer-Verlag - 1995. - V. 26.
17 Dineykhan M., Zhaugasheva S.A., Bekbaev A. K. Determination of the energy spectrum of a three-body Coulomb system with relativistic corrections // PHYSICAL REVIEW A Volume 87, № 052506, p. 1-12, 2013.
18 Ishmukhamedov I. S., Valiolda D. S., and Zhaugasheva S. A. Description of ultracold atoms in a one-dimensional geometry of a harmonic trap with a
realistic interaction // Physics of Particles and Nuclei Letters, Volume
11, Issue 3, p. 238-244 (2014).
19 Жаугашева С.А., Ишмухамедов И.С., Валиолда Д.С., Жусупова Н., Ультра суық атомдарды шынайы әсерлесуі бар гармоникалық тұзақтың бір өлшемді геометриясында бейнелеу // Известия НАН РК, серия физико – математическая, 2015г., том 3, № 301 (2015), 120 – 125стр.
20 Питаевский Л.П. Конденсаты Бозэ-Эйнштейна в поле лазерного излучения // УФН. –2006. - т. 176. -C. 345-364.
21 Chin, Grimm R., Julienne P.S. and Tiesinga F.,Feshbach E. Resonances in Ultracold Gases // Rev. Mod. Phys. - 2010. - P. 82 – 1225.
22 Haller E., Mark M. J., Hart R., Danzl J. G., Reichsollner L., Melezhik V., Schmelcher P. and Nagerl H.C. Confinement-Induced Resonances in Low-Dimensional Quantum Systems // Phys. Rev. Lett. - 2010. - P. 153203.
23 Peng S.-G., Hu H., Liu X.-J. and Drummond P.D. Confinement-Induced Resonances in Anharmonic Waveguides // Phys. Rev A 84.-2011. - P. 043619.
24 Bergeman T., Moore M.G., Olshanii M. Atom-Atom Scattering in the Presence of a Cylindrical Harmonic Potential: Numerical Results and an Extended Analytic Theory // Phys. Rev. Lett. – 2003. - P. 163201.
25 Dineykhan M., Zhaugasheva S.A., Toinbaeva N.Sh. // Jour.Phys.B: At. Mol. Opt. Phys. - 2010. – Vol.43. - P.015003.
26 Saeidian S., Melezhik V.S., Schmelcher Mutlichannel P. Atomic Scattering and Confinement-Induced Resonances in Waveguides // Phys. Rev.- A 77.-2008. -P. 042721.
27 Busch T., Englert R.G., Rzazewski K. and Wilkens M. Two cold atoms in a harmonic traps // Foundations of physics 28(4). -2010. - P. 549-559.
28 Hermann M. R. and Fleck J. A. // Jr. Phys. Rev - A38.-1988.
29 Peng S.-G., Hu H., Liu X.-J. and Drummond P. Confinement-induced resonances in anharmonic waveguides // Physical Review A84.-2011. - P. 043619.
30 Shi-Guo Peng, Hui Hu, Xia-Ji Liu, Peter D. Drummond // Phys. Rev. - A 84.-2011. – P. 043619.
31 Валиолда Д.C., Ишмухамедов И.С., Жаугашева С.А., Описание ультрахолодных атомов в одномерной геометрии гармонической ловушки с реалистическим взаимодействием // Письма в ЭЧАЯ, 2014 г., том 11, №3 (187), стр. 390-400.
Қосымша 1
Осцилляторда өрнектелу әдісі. Негізгі күйдегі Шредингер теңдеуін Кулон потенциалында қолдану
Атомдық және ядролық потенциалдар тек радиус вектордың модуліне тәуелді болса, ондай потенциалдарды сфералық симметриялы потенциалдар деп айтамыз. Мұндай потенциалдардың мысалы ретінде кулон, гармоникалық осциллятор, Юкава потенциалдары жатады. Кез келген потенциал үшін ШТ-нен энергетикалық спектрін аналитикалық тұрғыдан анықтау мүмкін емес. Сондықтан біз ШТ шешетін жуықтау әдістерін қарастырамыз. Осы әдіс бойынша, кулондық потенциалдың энергетикалық спектрін анықтайық. Сонда сутегі атомы үшін Шредингер теңдеуі:
 (1)
(1)
деп жазылады. (2.51) теңдеуідегі кинетикалық энергияның операторын декарттық және сфералық координаттар жүйесінде:
 (2)
(2)
деп анықталады. Мұндағы  − орбиталдық момент операторы:
− орбиталдық момент операторы:
 . (3)
. (3)
Толқындық функция бұл кезде координаттық және бұрыштық бөліктерден тұрады:
 . (4)
. (4)
Толқын функция бұрыштық тәуелділігі сфералық гармоника функциясымен өрнектеледі және бұл функция орбиталдық моменттің меншікті функциясы болады немесе
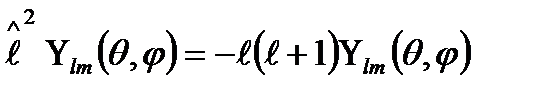 . (5)
. (5)
Нормалау шарты:
 (6)
(6)
болады. Осы нормалдау шартын пайдаланып және (2.52), (2.55) ескере отырып, қарапайым ықшамдаулардан кейін (2.51) өрнегінен радиалды Шредингер теңдеуін:
 (7)
(7)
түрінде жазамыз. Толқындық функция (ТФ)  болса
болса  ,
, 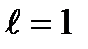 болса
болса  ,
,  болса
болса  күйлерді сипаттайды.
күйлерді сипаттайды.
Енді осы Шредингердің теңдеуін осцилляторда өрнектелу (ОӨ) әдісінде қалай анықтайтынын көрсетеміз, ол үшін  деп түрлендіру жасаймыз. Сонда бірінші және екінші дифференциалды:
деп түрлендіру жасаймыз. Сонда бірінші және екінші дифференциалды:
 (8)
(8)

түрінде анықтаймыз. (2.57) Шредингердің теңдеуіне (2.58) қойып, ықшамдаулар жүргізіп, ШТ:
 (9)
(9)
деп жазылады. Содан соң осцилляторда өрнектелу әдісінде толқындық функцияны:
 (10)
(10)
деп түрлендіреміз. Түрлендірілген ТФ үшін ШТ жазайық. Ол үшін бірінші және екінші дифференциалдарды:
 ; (11)
; (11) 

деп анықтаймыз. (2.60) түрлендіруді (2.59) қойып, қарапайым ықшамдаулардан кейін, радиалдық ШТ келесі түрде жазылады:
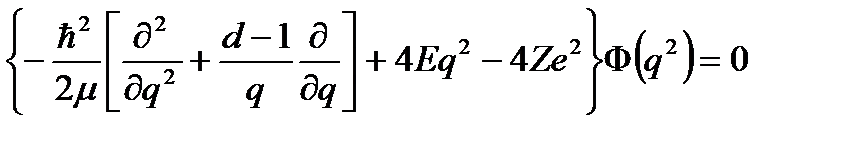 (12)
(12)
мұндағы  . (2.60) түрлендірудің нәтижесінде (2.59) теңдеуден
. (2.60) түрлендірудің нәтижесінде (2.59) теңдеуден  − өлшемді ШТ шығарып алдық. Осы ШТ потенциал гармоникалық осциллятор болып түрленді. ОӨ әдісінде
− өлшемді ШТ шығарып алдық. Осы ШТ потенциал гармоникалық осциллятор болып түрленді. ОӨ әдісінде  − өлшемді кеңістікке өткенде потенциал осциллятор болып түрленеді. Келесі теңдеуден
− өлшемді кеңістікке өткенде потенциал осциллятор болып түрленеді. Келесі теңдеуден  энергетикалық спектрін (ЭС) табамыз.
энергетикалық спектрін (ЭС) табамыз.
 . (13)
. (13)
(2.63) өрнекке сай энергетикалық спектр  теңдеуін қанағатандырады. Осы теңдеуден алғашқы гамильтонианның энергетикалық спектрін анықтаймыз. (2.63) теңдеуден ОӨ әдісінен қалай есептейтініне тоқталайық:
теңдеуін қанағатандырады. Осы теңдеуден алғашқы гамильтонианның энергетикалық спектрін анықтаймыз. (2.63) теңдеуден ОӨ әдісінен қалай есептейтініне тоқталайық:
 . (14)
. (14)
Осы Шредингер теңдеуінің шешімін табу керек.  деп алып, одан
деп алып, одан  -ны табамыз. Бұл әдісті осцилляторда өрнектеліну әдісі деп атайды. Бұл әдісте кванттық өріс теориясының әдісін кванттық механика есептерін шешуде қолданады. Ол үшін гамильтонианды:
-ны табамыз. Бұл әдісті осцилляторда өрнектеліну әдісі деп атайды. Бұл әдісте кванттық өріс теориясының әдісін кванттық механика есептерін шешуде қолданады. Ол үшін гамильтонианды:
 (15)
(15)
түрінде жазылады. Мұндағы  - еркін осциллятордың гамильтонианы. Бұл әдісті қолдану үшін каноникалық айнымалыларды, импульс және координатты,
- еркін осциллятордың гамильтонианы. Бұл әдісті қолдану үшін каноникалық айнымалыларды, импульс және координатты,  - туу және
- туу және 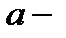 жою операторларымен өрнектейміз. Ол үшін келесі шарттар қанағаттандырылуы керек:
жою операторларымен өрнектейміз. Ол үшін келесі шарттар қанағаттандырылуы керек:
1) Гамильтониан қалыптандырылған түрде болуы керек немесе  тудыратын оператор сол жағында, ал
тудыратын оператор сол жағында, ал 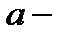 жою операторы оң жағында орналасуы керек;
жою операторы оң жағында орналасуы керек;
2) Қалыптандырылған түрдегі әсерлесу гамильтонианда каноникалық координаттың квадраттық түрдегі оператордың коэффициенті нөлге тең болуы керек. Бұны ОӨ әдісінің шарты деп атайды.
Енді осы шарттарға сәйкес каноникалық айнымалыларды туу және жою операторлары арқылы өрнектейік:
 (16)
(16)
(2.64) теңдеудегі гамильтонианға (2.66) қойып, гамильтонианды қалыпты түрде жазамыз. 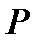 және
және  каноникалық айнымалыларды
каноникалық айнымалыларды 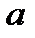 мен
мен  операторлары арқылы өрнектеп, ықшамдаймыз, сонда:
операторлары арқылы өрнектеп, ықшамдаймыз, сонда:
 (17)
(17)

Каноникалық айнымалыларды қалыпты түрде жаздық. Толық гамильтониан:
 (18)
(18)
немесе
 (19)
(19)
түрінде жазылады. Мұндағы  − еркін осциллятордың гамильтонианы
− еркін осциллятордың гамильтонианы
 , (20)
, (20)
ал  ,
,  − өлшемді кеңістігіндегі, нөлдік жуықтау энергиясы:
− өлшемді кеңістігіндегі, нөлдік жуықтау энергиясы:
 . (21)
. (21)
 - әсерлесу гамильтонианы кулон потенциалы үшін нөлге тең.
- әсерлесу гамильтонианы кулон потенциалы үшін нөлге тең.  әсерлесу гамильтонианында квадраттық мүшелер болмауы керек деген шартты қанағаттандыру үшін
әсерлесу гамильтонианында квадраттық мүшелер болмауы керек деген шартты қанағаттандыру үшін  - коэффициентін нөл деп алып, содан
- коэффициентін нөл деп алып, содан 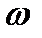 -ны табатын теңдеу шықты,
-ны табатын теңдеу шықты,
 . (22)
. (22)
Осы теңдеуден
 . (23)
. (23)
Алғашқы гамильтонианның энергетикалық спектрін есептейміз:
 . (24)
. (24)
Бұл әдеттегі кулон потенциалының энергетикалық спектрі. Енді аналитикалық түрде есептелмейтін потенциалдар үшін ШТ осы әдіс шеңберінде қалай шешетінін көрсетейік.
[1]Екінші суреттегі потенциалдың шетіндегі кедір-бұдырлар нүктелердің саны салыстырмалы аз болуымен шартталған






