Ангармоникалық конфайнменті бар нақты потенциал
(2.1)
[30] жұмыста негізгі және қозған күйлер үшін ангармоникалық түзетуді ескеріп, ауытқу теориясы аясында энергетикалық спектр анықталған. Аз параметрлердің деңгейі бойынша осцилляторда өрнектелу (ОӨ) әдісі [17] аясында (4.1) потенциалы үшін энергетикалық спектр анықтаймыз. (2.1) бірөлшемді потенциал үшін Шредингер теңдеуі мына түрде жазылады:
(2.2)
Тұзақ потенциалын 
дәрежесі бойынша жіктесек:
(2.3)
мұндағы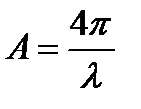 
, алынған нәтижелерімізді басқа теориялық жұмыстардың нәтижелерімен салыстыру үшін келесі параметрлерді тағайындаймыз:
(2.4)
мұндағы 
- тұзақтың ангармоникалылық дәрежесінің мағынасын білдіреді, және оның мәнін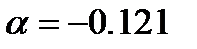 
таңдап аламыз, ол [29] жұмыста көрсетілген мәнмен сәйкес (2.3) теңдеуін ОӨ әдісімен шешу нәтижелері 1-кестеде көрсетілген. Енгізілген 
- және 
-параметрлерін ескеріп, тұзақтың нақты потенциалын қайта жазайық:
(2.5)
Гамильтонианда кинетикалық энергиясын сақтайтын, массалар орталығының және салыстырмалы қозғалыстың айнымалыларына көшейік:
(2.6)
Есепті ұзындық және энергия бірліктері 
формуласымен берілетін бірлікте шешеміз. Бұл айнымалыларда (1.1) гамильтониан келесі түрге ие болады:
(2.7)
Тек бірінші жоғалмайтын ангармоникалық мүшесін ескерген жағдайда 
потенциалы келесі түрге келеді:
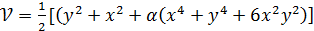(2.8)
ал жалпы жағдайда ол:
(2.9)
болған кездегі (2.8) және (2.9) потенциалдар формуласын қарастырайық:
Сурет 8 – (2.8) және (2.9) потенциалдар графиктері
Екі потенциал да тосқауылдың ақырғы биіктігіне ие болады, ол энергия деңгейлерінің кеңеюіне әкеледі. Ол үшін потенциалдық тосқауылдың максимумында шексіз өткізбейтін тосқауыл қойылды. Сонымен қатар, әртүрлі үшін, тосқауыл орны түрленеді. Потенциал жинақталған аймақты, қарапайымдылық үшін, 
радиусының шеңбері ретінде таңдап аламыз.
2-суретте 
үшін 
шекарасының өзгеруі кезіндегі (2.8) потенциалының өзгерісі бейнеленген. Мұнда үш жағдай көрсетілген: 
; 3.5; 4.5:
Сурет 9 – аймағында берілген 
потенциалы
Оптикалық тұзақтың негізінде бірнеше потенциалдық шұңқыры болады, алайда, менің мақсатым бір шұңқыр аясында стационарлық деңгейлерді есептеу болып табылады. 2-суреттегі графиктерден 
2.7 мәнінен асатын r мәндері кезінде потенциалдың кеми бастайтыны көрініп тұр, потенциалдық тосқауылдың максимумындағы өткізбейтін тосқауыл есебі шығады. Осылай берілген тосқауылмен, 2.7 және кезіндегі потенциал келесі түрде болады:
Сурет 10 – Гамильтониан спектрін сандық әдіспен есептеу кезінде қолданылатын, Vnum(x,y)[1] тосқауылы бар потенциал
Осылайша, сандық есептеулерде (2.8) потенциалдың орнына келесі потенциалды қолданамыз:
(1.9)
және (2.9) потенциалына ұқсас, оны 
түрінде белгілейміз. Нәтижесін 1-кестеге жазамыз, онда 
және потенциалдар шегі келтірілген.
Кесте 1 – және потенциалдар шегі
|
|
| |
| 
| |
| -0.03025 | 2.7 | 3.3 |
| -0.06 | 2.4 |
Кесте 2 – (2.3) потенциалындағы энергетикалық спектрі үшін есептеулер нәтижелері. 
- бірінші ретті анграмоникалыққа дейінгі (2.3) өрнегінде көрсетілген потенциалдың жіктелуіне сәйкес келеді; 
- (2.3) тұзақтың нақты потенциалына сәйкес келеді. Жақшада көрсетілген мәндер [29] жұмысының нәтижелері.
|
| |||
| 
| 
| 
|
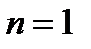
| 0.47428963 (0.4773125) | 1.31766727 (1.3865625) | 2.05997814 (2.2050625) |
| |||
|
|
|
|
|
|
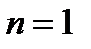
| 0.476255 | 1.3435 | 2.15623 |
Ангармоникалық оптикалық тұзақтағы спектрді есептеу үшін екіөлшемді Шредингер теңдеуін (ШТ) сандық шешу әдістерін өрнектейік. Бастапқы гамильтонианның түрі:
(2.6)
Қарапайымдылық үшін гармоникалық тұзақ үшін шешу сызбасын келтірейік. Бұл жағдайда гамильтонианның түрі:
(2.7)
Салыстырмалы координатаға және массалар орталығы координатасына ауыса отырып:
(2.8)
(5.2) өрнегіндегі гамильтониан келесі түрге түрленеді:
(2.9)
салыстырмалы координатасы үшін (2.9) гамильтонианы бар ШТ сандық есептеу үшін алтыншы ретті дәлдікпен ақырғы-айырмалы туынды аппроксимациясын пайдаланамыз, ал 
массалар орталығының координатасы үшін – екінші ретті аппроксимацияны пайдаланамыз. Тензорлық әсерлесуі бар ШТ есептеуге арналған бағдарламаны өзіміздің жағдай үшін түрлендіреміз, онда шашырау каналдары ретінде айнымалылары бойынша дискреттелу қолданылады. координатасы үшін алынған теңдеулер жүйесі келесі матрицалық түрге ие болады:
(2.10)
Мұндағы
(2.11)
ал 
- 
айнымалысы бойынша дискреттелу қадамы. Осылайша, (2.9) ШТ-нің толық шешімі үшін сәйкес шекаралық шарттарды ескере отырып, айнымалысы бойынша дискреттеу қажет.
2.1 Ангармоникалық тұзақтардағы екіатомдық кванттық жүйелердің ені мен өзгерістері
Тұзақтың ангармонизм эффекттерінің 
салыстырмалы қозғалыс және 
массалар орталығы айнымалыларының бөлінбеуіне әкелетін екібөлшекті кванттық жүйе спектріне әсерін зерттеу үшін біз квазипотенциалдық модель өңдедік. Бұл әдісте V(x) атомаралық әсерлесу g тұрақтысы бар 
псевдопотенциалмен бейнеленеді, ол әртүрлі ультрасуық процестер динамикасына сай сипаттайды. Бұл әдіс пайда болған екіөлшемді Шредингер теңдеуін ақырғы айырмалар әдісі көмегімен сандық зерттеуге мүмкіндік береді:
Ақырғы айырмалар әдісінде пайда болатын меншікті мәндерге алгебралық есеп
стандартты сандық әдіс көмегімен шешуге жол береді. Сонымен қатар, бұл әдіс ``complexrotationmethod''-ге 
жалпылануына жол береді, ол сондай-ақ ангармоникалық тұзақтың ақырғы ені есебінен 
екіатомдық жүйе деңгейлерінің енін есептеуге мүмкіндік береді
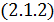
Берілген әдіс аясында кванттық жүйелер деңгейлерінің енін есептеу үшін стационар емес Шредингер теңдеуін шешу көмегімен баламалы алгоритм де мүмкін болады:
мұндағы 
- бастапқы уақыттағы кванттық жүйенің толқындық функциясы (v – жүйе күйін сипаттайтын кванттық сан), ол үшін «өткізбейтін» тосқауылмен шексіз биіктігі және ені бар гармоникалық тұзақтың стационар жағдайына сәйкес келетін шешім алған ыңғайлы болып табылады. t>0 кезінде ангармонизм қосу тұзақ қабырғасының ақырғы еніне әкеледі (қабырға ені 
параметрімен беріледі) және, салдарынан, E деңгейінде еніне әкеледі. 
аймағына (3) стационар емес теңдеуін интегралдап бастапқы енін анықтауға болады
(2.1.4)
Уақыт бойынша интегралдау ақырғы айырым әдісіне ұқсас t айнымалысы бойынша 
айырмалық торда В.С.Мележиктің жұмыстарында өңделген және ұсынылған компонентті ыдырау әдісі көмегімен жүзеге асырылады.
енін анықтап кванттық жүйенің өмір сүру уақытын бағалауға болады
(2.1.5)
Бұл кезде жүйенің ыдырау жылдамдығы
(2.1.6)
Басқа жағынан, бұл әдіс есептеуді бақылауға мүмкіндік береді, өйткені гармоникалық тұзақтың (
) шекті жағдайында есептегі айнымалылар бөлінеді, ол екі тәуелсіз бірөлшемді теңдеулерге келтіріледі
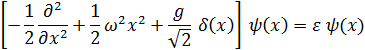
(2.1.7)
(мұндағы 
) және біздің модель бұл шекті жағдайда [8] жұмыста қарастырылған Буштың аналитикалық моделіне сәйкес келеді.
Шредингердің 2D бастапқы теңдеуіндегі туындыларды x және X айнымалылары бойынша ақырғы-айырмалы жуықтау үшін интегралдау қадамы h болатын біртекті 
айырмалық торлар енгізіледі. 
тармағынан басқа әрбір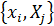 
нүктедегі туындыларды жуықтау үшін 
дәлдік ретін қамтамасыз ететін стандартты үш нүктелік формулалар қолдандық. 
тармағы арнайы қарастыруды қажет етеді. Бұл жерде (2.1.7) Шредингер теңдеуі келесі өрнекке ауыстырылады
(2.1.8)
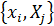айырмалық торда болмайтын (2.5) теңдеуінен 
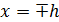нүктелерді алып тастау үшін мына жуықтауды қолдандық:
,
ол 
есептегіш сызбасының дәлдік ретін сақтайды.
интегралдарын Симпсон бойынша есептеу кезінд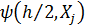е 
және 
шамалары пайда болады, олар
формулалары көмегімен есептелді, сондай-ақ талап етілген дәлдік ретін береді.
Осылайша, үш диагоналды құрылымға ие болатын (2.1.1) алгебралық теңдеулер жүйесін аламыз
Соңғы жағдай алынған алгебралық есептерді сандық шешу үшін экономикалық алгоритмдер құру үшін қолданылды.
Келесі бөлімде кейбір есептеулер нәтижелерін келтіреміз, сондай-ақ алынған нәтижелердің 
шегінде сәйкес келулеріне зерттеулер жүргіземіз.
Ұқсас сызба стационар емес Шредингер теңдеуін сандық шешу үшін қолданылады (3)
(2.1.8)
Оны біз келесі тарауда тұзақ ангармонизмінің екіатомдық молекулалардың пайда болу жылдамдығына әсерін зерттеу үшін қолданамыз.
