Сгенерируем выборку (столбец) из 20 наблюдений над нормальной случайной величиной со средним а = 10 и дисперсией s2 = 4 и определим доверительные интервалы для а с уровнем доверия РД: 0.8, 0.9, 0.95, 0.98, 0.99, 0.999. Выполняется командой
Analisis - Descriptive staistics - в поле Statistics выбрать Conf. Limits for means и указывать значение Alpha error: 80 (90, 95 т.д.).
Выполнение в пакете SPSS
Уровень доверия
а) Генерация k = 50 выборок по n = 10 наблюдений, нормально распределенных с параметрами: среднее а = 10, дисперсия s 2 = 4.
Выборки поместим в таблицу с 50 строками (выборками) и 10 (объем выборки) столбцами (при таком размещении сокращается работа по генерации наблюдений). В первом столбце таблицы выделяем клетку в 50-й строке и вводим точку. 50 строк создано.
Переименуем 1-й столбец:
Data - Define Variable - Name: x 01 - OK
Сгенерируем наблюдения:
Transform - Compute - Target Variable (целевая переменная): x 01, Numeric Expression (числовое выражение):
NORMAL (2) + 10
это выражение вводим кнопками окна - ОК.- Change? - OK.
В первом столбце наблюдения получены. Повторяем, начиная с Transform, заменив х 01 на х 02; и так 9 раз (5 нажатий на 1 столбец). Матрица наблюдений получена.
б) Оценка средних.
В пакете статистики определяются по столбцам (переменным), поэтому выборки-строки преобразуем транспонированием в выборки-столбцы:
Data - Transpose...- все имена переменных переносим в правый список Variables (выделяем все, нажимаем кнопку-стрелку) - ОК.
Теперь имеется 50 столбцов - выборок по 10 строк - наблюдений. Первый столбец case - lbl можно удалить:
выделим его - Edit - Clear (или клавиша Delete).
Определим среднее по выборкам:
Statistics - Summarize - Descriptives...- перенесем имена всех столбцов в правый список, отметим Display labels (имена показывать) - Options...- отметим только Mean; îòìåòèì Display Order: Name (показывать по порядку) - Continue - OK.
В окне Output получаем столбец Mean результатов. Если в столбце есть пропуски или текст, удаляем лишние строки, чтобы столбец результатов состоял из 50 строк с числами.
Сохраним столбец результатов в буфере операцией Copy. Снова транспонируем матрицу (чтобы в дальнейшем не было пустых блоков). Получили 10 числовых столбцов и 50 строк (выборок).
Выделяем 1-й справа свободный столбец и с помощью Edit - Paste помещаем в него столбец средних. Присвоим ему имя as:
выделим его - Data - Define Variable - Name: as
в) Определение столбцов а1 и а2 левых и правых концов доверительных интервалов.
Пусть РД = 0.9, квантиль порядка (1 + РД)/2 = 0.95 есть fР = 1.645. Вычислим левые концы:
Transform - Compute - Target Variable: a1, Numeric Expression (по (5), учитывая, что s = 2): as – 1.645 * 2/ SQRT (10).
Аналогично вычислим левые концы а2.
г) Результаты k = 50 испытаний доверительного интервала представим графически, предварительно образовав столбец а с истинным значением 10 параметра; затем:
Graphs - Line...- Multiple (несколько графиков), Values of individual cases - Define - Line Represent (представить линии): а, а1, а2 - ОК.
Наблюдаем график, из которого видно, сколько интервалов из 50 не содержат истинное значение. Записываем его; оно должно находиться приближенно в пределах 5 ± 2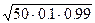 
» 5 ± 4. График распечатаем или сохраним: File - Save As...
д) Пусть РД = 0.99; тогда fР» 2.57; если РД = 0.999, то fР» 3.29. Повторим пп. в) и г) для этих значений РД. Убеждаемся, что с ростом РД число ошибок уменьшается, но ширина интервала увеличивается (чем надежнее гарантия, тем меньше она гарантирует).
Задание: провести аналогично k = 50 испытаний доверительного интервала (7) - (9) для случая неизвестной дисперсии.
