Уровень доверия
а) Сгенерируем массив z размером k´n=50´10=500 наблюдений, распределенных нормально с параметрами а=10, s2 = 22 = 4 (процедурой H.5. Random Number Generation) и образуем k=50 выборок объема n=10 т.е. матрицу х размерности 10 х 50: процедура A.2. File Operation, операция J.Update, оператором
10 50 RESHAPE z
б) Оценим средние (массив xs длиной k=50) по (1) процедурой A.2, операция J, оператором
SUM x/10
в) Определим квантили fp порядков (1+ РД)/2 (0.95, 0.995, 0.9995) нормального распределения N(0,1):
H.4. Critical Values (критические значения) - (Dist. Number: 14 (Normal)) - F6 - (mean: 0, std. deviation: 1) - F6 - (Area at or below: 0.95) - F6.
г) Определим массив a1 длины k = 50 левых концов интервалов по (5): процедура A.2, операция J, оператор
xs - fp *s / SQRT (n)
д) Аналогично определим массив а2 правых концов интервалов.
е) Результаты k = 50 испытаний доверительных интервалов проанализируем по графику, полученному с помощью процедуры E.2. Multiple X-Y Plots, задав
X: COUNT 50
Y: a1
Y: a2
Y: 50 REP 10
Последняя строка потребовалась для изображения истинного значения а=10.
Определим, сколько раз из k= 50 доверительный интервал оказался неверным. Это сделаем для трех значений РД (соответственно fp).
Графики для РД = 0.9 и РД = 0.99 распечатаем.
Задание. Провести аналогично k =50 испытаний доверительного интервала (7) - (9) для случая неизвестной дисперсии.
Интервалы для параметров нормального распределения
Сгенерируем выборку из 20 наблюдений над нормальной случайной величиной со средним а = 10 и дисперсией s2 = 4 и определим доверительные интервалы для а и s с уровнем доверия РД: 0,8, 0,9, 0,95, 0,98, 0,99. Выполняется в процедурном блоке G. Estimation and Testing процедурой 1. One-Sample Analysis Результаты выпишем в виде таблицы. C ростом РД интервал расширяется, с ростом n - уменьшается.
3. Выполнение в пакете STATISTICA
Уровень доверия
Работаем в модуле Basic Statistics and Tables.
а) Генерируем k = 50 выборок по n = 10 наблюдений, нормально распределенных с параметрами: среднее а = 10, дисперсия s2 = 4.
Создадим таблицу с 50 строками (выборками) и 10 (объем выборки) столбцами:
File - New Data - File Name: Doverit (например)- ОК.
Создана таблица 10v ´ 50c; добавим 40 строк после 10-й:
Кнопка Vars ( или Edit - Cases) - Add - Number of Cases to Add: 40, insert after Case: 10 - OK.
Сгенерируем наблюдения:
Vars - All Specs - в появившейся таблице Variables Doverit.sta в 4-м столбце Long name выделим 1-ю клетку и запишем в ней
= Vnormal (Rnd (1); 10, 2)
и перенесем эту запись в строки со 2-й по 10-ю:
Edit - Copy (или кнопка Copy) (копирование в буфер),
затем выделим следующую клетку и
Edit - Paste (или кнопка Paste).
Закроем окно. Выполним назначения:
Edit - Variables - Recalculate...(или кнопка Х =?).
б) Оценим средние:
Edit - Block Stats/Rows - Means.
Образован 11-й столбец MEAN. Присвоим ему имя xs:
выделим столбец MEAN - Vars - Current Specs...-Name: xs - OK.
в) Определим квантили fp порядков (1 + РД)/ 2 (0.95, 0.995, 0.9995) нормального N (0, 1) распределения:
Analisis-Probability Calculator - в окне устанавливаем Distribution Z (Normal), выделим Inverse, p: 0.95 - Compute; результат в поле Z: 1.645.
Аналогично определим fp для остальных вероятностей (2.57 и 3.29).
г) Определим по (5) столбцы а1 и а2 левых и правых концов доверительных интервалов.
Выделим заголовок столбца xs - Vars - Add - Number...: 2, after: xs - OK - выделим новый столбец - Vars - Current Specs - Name: A1 (левые концы), Long name:
= xs - 1,65 * 2 / Sgrt(10)
После ОК получаем столбец левых концов. Аналогично получаем столбец а2 правых концов.
д) Результаты k = 50 испытаний доверительного интервала представим графически:
выделим столбец а1 и а2 - Graphs - Custom Graphs - 2D Graphs - OK (соглашаемся с предложениями).
Видим график (рис.1), по которому определяем число экспериментов (6 из k = 50), в которых интервал не содержит истинного значения параметра. Можем определить координаты любой точки на рисунке, поставив на нее стрелку: координаты в верхнем левом углу. Распечатаем график.
е) повторим пп. г) и д) для двух других значений доверительной вероятности.
Задание: Провести аналогично k = 50 испытаний доверительного интервала (7) - (9) для случая неизвестной дисперсии (рис.2 для Р Д = 0.9; 5 ошибок).

Рис. 1.
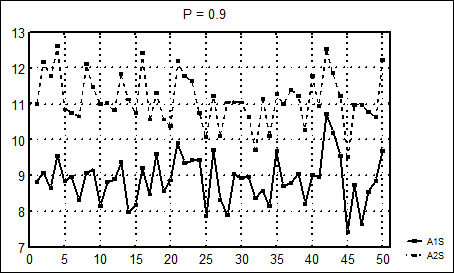
Рис.2.






