Работа N4. Доверительные границы и интервалы
результатом применения точечной оценки a(x1,...,xn) является одно числовое значение; оно не дает представления о точности, т.е. о том, насколько близко полученное значение к истинному значению параметра. Интуитивно ясно, что такое представление может дать, например, дисперсия оценки, так что истинное значение должно находиться где-то в пределах
a ± (2¸4) 
Внесем уточнения.
Основные положения
Определения и построение интервалов
Пусть (x1,...,xn) º x - n независимых наблюдений над случайной величиной с законом распределения F (z / a), зависящим от параметра a, значение которого неизвестно.
Определение 1. Функция наблюдений a1 (x1,...,xn) (заметим, что это случайная величина) называется нижней доверительной границей для параметра a с уровнем доверия РД (обычно близким к 1), если при любом значении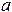 
P { a1 (x1,...,xn)£ a }³ PД
Определение 2. Функция наблюдений a2 (x1,...,xn) (случайная величина) называется верхней доверительной границей для параметра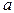 
с уровнем доверия РД, если при любом значении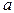
P { a2 (x1,...,xn)³ a }³ PД.
Определение 3. Интервал со случайными концами (случайный интервал)
I (x) = (a1 (x), a2 (x)),
определяемый двумя функциями наблюдений, называется доверительным интервалом для параметра a с уровнем доверия РД, если при любом значении a
P { I (x)' a } º P{ a1 (x1,...,xn)£ a £ a2 (x1,...,xn)} ³ PД,
т.е. вероятность (зависящая от a) накрыть случайным интервалом I (x) истинное значение a - велика: больше или равна РД.
Построение доверительных границ и интервалов. Для построения доверительного интервала (или границы) необходимо знать закон распределения статистики z=z (x1,...,xn), по которой оценивается неизвестный параметр (такой статистикой может быть оценка z = a (x1,...,xn)). Один из способов построения состоит в следующем. Предположим, что некоторая случайная величина j = j(z, a), зависящая от статистики z и неизвестного параметра a такова, что
1) закон распределения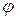 
известен и не зависит от a;
2) j(z, a) непрерывна и монотонна по .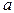
Выберем диапазон для 
- интервал 
так, чтобы попадание в него было практически достоверно:
P { f1 £j(z, a) £ f2 }³ PД, (1)
для чего достаточно в качестве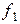 
и 
взять квантили распределения уровня (1- РД)/2 и (1+ РД)/2 соответственно. Перейдем в (1) к другой записи случайного события, разрешив неравенства относительно параметра a; получим (полагая, что монотонно возрастает по ):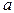
P { g (z, f1)£ a £ g (z, f2) }³ PД.
Это соотношение верно при любом значении параметра a (поскольку это так для (1)), и потому, согласно определению, случайный интервал
(g (z, f1), g (z, f2))
является доверительным для a с уровнем доверия РД. Если убывает по 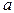, интервалом является (g (z, f2), g (z, f1)).
Для построения односторонней границы для a выберем значения 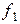и так, чтобы
P {j(z, a) ³ f1 }³ PД, f1=Q (1 - PД)
или P {j(z, a) £ f2 }³ PД , f2 = Q (PД),
где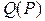 
- квантиль уровня 
. После разрешения неравенства под знаком получим односторонние доверительные границы для a.
Пример. Доверительный интервал с уровнем доверия РД для среднего a нормальной совокупности при известной дисперсии s 
.
Пусть x 
,..., xn - выборка из нормальной N (a, s 
)совокупности. Достаточной оценкой для а является
a = a (x 
,...,xn) = 
,
распределенная по закону N (a, 
); пронормируем её, образовав случайную величину
, (2)
которая распределена нормально N (0, 1)при любом значении а.
По заданному уровню доверия РД определим для j отрезок [- fp, fp ] так, чтобы
, (3)
т.е. fp - квантиль порядка (1+ РД)/2 распределения N (0,1); заметим, что j зависит от а, но (3) верно при любом значении а. Подставим в (3) выражение для j из(2) и разрешим неравенство под знаком вероятности в (3) относительно а; получим соотношение
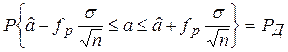, (4)
верное при любом значении а. под знаком вероятности две функции наблюдений
, 
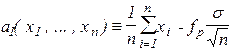( 5)
определяют случайный интервал
I (x1,..., xn) =(a1 (x1,..., xn), a2 (x1,..., xn)), (5a)
который в силу (4) обладает тем свойством, что накрывает неизвестное значение параметра а с большой вероятностью РД при любом значении а, и потому, по определению доверительно интервала, он является доверительным с уровнем доверия РД.
В общем случае случайную величину j в (1) можно построить следующим образом. Определим функцию распределения F (z / a)статистики z (F, конечно, зависит от а). Для непрерывной z случайная величина j (z, а) º F(z / a),как нетрудно видеть, распределена равномерно на отрезке [0, 1] при любом значении а; приняв f1= (1- PД)/ 2, f2 = (1+PД)/ 2, будем иметь в качестве (4)
P { f 1 £ F (z / a) £ f 2} = PД.
Для дискретной z ситуация аналогична.
Можно рассуждать иначе: при любом фиксированном значении а определим отрезок [ z 1(a), z 2(a)] так, что
P{ z1 (a)£ z £ z2 (a)} ³ РД; (6)
ясно, что в качестве z1 и z2 можно взять квантили, т.е. определить из условий
F (z !/ a)=(1- РД)/ 2, F (z 2/ a)=(1+ РД)/ 2.
Если z1 (a) и z2 (a) монотонно возрастают по а, то, разрешив два неравенства под знаком Р в (6) и учитывая, что z 1(a) < z 2(a),получим:
P { z 2-1(z) £ a £ z1-1(z) } ³ РД ,
вверное при любом а; ясно, что интервал (z2-1 (z), z1-1 (z)), определяемый двумя функциями от z, является доверительным с уровнем доверия Р Д.
Уровень доверия
Уровень доверия РД означает, что правило определения интервала дает верный результат с вероятностью РД, которая обычно выбирается близкой к 1, однако, 1 не равно.Убедимся статистически на примере в том, что доверительный интервал с уровнем доверия РД может не содержать (с малой вероятностью 1- РД) истинное значение параметра.
Пример. рассмотрим приведенный в (5) случайный интервал I(x1,..., xn), который при любом значении а накрывает это значение с большой вероятностью РД:
Р { I (x1,...,xn) ' a } = Р Д,
и потому, если пренебречь возможностью осуществления события a Ï I, имеющего малую вероятность (1-Р Д), можно считать событие a Î I(x1,...,xn) практически достоверным, т.е. можно верить тому, что вычисленный по конкретным наблюдениям x1,...,xn интервал I содержит неизвестное значение параметра а.
Испытаем интервал (5) на 50 выборках объема n= 10 для трех уровней доверия Р Д: 0.9, 0.99, 0.999 (соответственно, три значения fp).
При Р Д = 0.9 число неверных из k =50 результатов окажется в окрестности 5, так как среднее число неверных
k (1- Р Д) = 5;
при Р Д =0.99 появление хотя бы одного неверного из k =50 весьма вероятно: вероятность этого события
1- Р Д k=1-0.9950» 0.61;
при Р Д =0.999 появление хотя бы одного неверного весьма сомнительно: вероятность этого события
1- Р Д k=1-0.99950» 0.05.
Задание.
1. Определить, сколько раз из k =50 доверительный интервал оказался неверным;.это сделаем для трех значений Р Д. Графики для Р Д =0.9 и Р Д =0.99 распечатать. Выполнение в пакетах см. в пп. 2 - 4.
2. Провести аналогично 50 испытаний доверительного интервала (7) - (9) для случая неизвестной дисперсии.
