| Типы систем | Статические | Динамические | |||||||
| Дискретные по U.Y | Непрерывные по U.Y | Дискретные по Т | Непрерывные по Т | ||||||
| Дискретные по U, Y | Непрерывные по U,Y | Дискретные по U,Y | Непрерывные по U, Y | ||||||
| Математический аппарат описания | Схемы независимых испытаний | Регрессионные модели | Марковские цепи, стохастические автоматы | Стохастические разностные уравнения | Системы массового обслуживания | Стохастические дифференциальные уравнения | |||
| Методы оценки параметров и анализа | Стохастические оценки вероятности, дисперсионный анализ | Регрессивный анализ | Статистическое моделирование | Статистическое оценивание состояний и параметров, анализ стохастической устойчивости | Теория массового обслуживания, имитационное управление | Теория устойчивости | |||
| Методы синтеза | Стохастическое программирование | Планирование эксперимента, стохастическое программирование | Динамическое программирование | Динамическое программирование | Перебор, методы оптимального управления | Оптимальное и адаптивное управление | |||
| Области применения | Задачи выбора из конечного числа вариантов (испытания) | Обработка результатов измерений, испытаний | ЭВМ | Импульсные и цифровые САУ | Системы обслуживания (вычислительные системы, ГАП и т.д.) | САУ, механические, тепловые, электронные и другие процессы | |||
Примечание: U - множество входов, Y - множество выходов системы.
Закон больших чисел гласит, что если 
– случайные величины с математическим ожиданием 
и дисперсией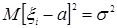 
, то
(30)
при достаточно больших N. Это говорит о принципиальной возможности сколь угодно точной оценки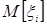 
, по измерениям. Центральная предельная теорема, уточняющая (40), утверждает что
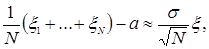(31)
где ξ - стандартная нормально распределенная случайная величина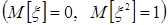 
.
Если величина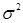 
неизвестна, то следует заменить в (41) σ на оценку
где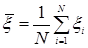 
При этом величина ξ будет распределена уже не нормально, а по закону Стьюдента, который при N ≥ 20 практически неотличим от нормального
Поскольку распределение величины хорошо известно и затабулировано (например, известно, что Р {| ξ |>1}=0.32, Р {| ξ |>2}=0.05, Р {|ξ|>3}=0.03), то соотношение (31) позволяет вычислять погрешность оценки. Пусть, например, требуется найти, при каком числе измерений погрешность оценки их математического ожидания с вероятностью 0.95 окажется меньше, чем 0.01, если дисперсия каждого измерения равна 0.25. Из (31) получаем, что должно выполняться неравенство
откуда N > 10000.
Разумеется, формулировкам (30), (31) можно придать более строгий вид и это легко может быть сделано с помощью понятий вероятностной сходимости. Трудности возникают при попытке проверить условия этих строгих утверждений.
Например, в законе больших чисел и центральной предельной теореме требуется независимость отдельных измерений (реализаций) случайной величины и конечность ее дисперсии. Если эти условия нарушаются, то могут нарушаться и выводы. Например, если все измерения совпадают: 
то, хотя все остальные условия выполняются, об усреднении не может быть и речи.
Другой пример: закон больших чисел несправедлив, если случайные величины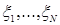 
распределены по закону Коши (с плотностью распределения 
, не обладающему конечными математическими ожиданием и дисперсией. А ведь такой закон встречается в жизни. Например, по Коши распределена интегральная освещенность точек прямолинейного берега равномерно вращающимся прожектором, находящимся в море (на корабле) и включающимся в случайные моменты времени.
Но еще большие трудности вызывает проверка обоснованности самого Употребления термина «случайный». Что такое случайная величина, случайное событие и т.д.? Часто говорят, что событие А случайно, если в результате эксперимента оно может наступить (с вероятностью р) или не наступить (с вероятностью 1 - р). Все, однако, не так просто. Само понятие вероятности может быть связано с результатами экспериментов лишь через частоту его наступления в некотором ряде (серии) экспериментов: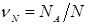 
, где NA - число экспериментов, в которых событие наступило, N - общее число экспериментов. Если числа 
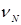при Достаточно большом N приближаются к некоторому постоянному числу рА:
, (32)
то событие А можно назвать случайным, а число р - его вероятностью. При этом частоты, наблюдавшиеся в различных сериях экспериментов, должны быть близки между собой (это свойство называется статистической устойчивостью или однородностью). Сказанное относится и к понятию случайной величины, Поскольку величина ξ является случайной, если случайными являются события { а<ξ<b } для любых чисел а, b. Частоты наступления таких событий в длинных сериях экспериментов должны группироваться около некоторых постоянных значений.
Итак, для применимости стохастического подхода должны выполняться следующие требования:
· массовость проводимых экспериментов, т.е. достаточно большое число;
· повторяемость условий экспериментов, оправдывающая сравнение результатов различных экспериментов;
· статистическая устойчивость.
Стохастический подход заведомо нельзя применять к единичным экспериментам: бессмысленны выражения типа «вероятность того, что завтра будет дождь», «с вероятностью 0.8 ЦСКА выиграет кубок УЕФА» и т.п. Но даже если массовость и повторяемость экспериментов имеются, статистической устойчивости может и не быть, а проверить это – непростое дело. Известные оценки допустимого отклонения частоты от вероятности основаны на центральной предельной теореме или неравенстве Чебышева и требуют дополнительных гипотез о независимости или слабой зависимости намерений. Опытная же проверка условия независимости еще сложнее, так как требует дополнительных экспериментов.
Принципы выбора модели
В заключение попытаемся сформулировать некоторые правила, помогающие на этапе выбора структуры ММ, - принципы выбора модели. Первейшим из них является принцип простоты: из различных вариантов структуры ММ сначала следует попробовать простейший. Например, если исследуется сложная динамическая (инерционная) система, то сначала нужно проверить, нельзя ли ограничиться статической моделью, не учитывающей динамику.
Как указывалось, статическую модель заведомо можно применить, если система устойчива, изменения ее входов достаточно медленны, а выходы измеряются достаточно редко. Однако эти требования не обязательны и в рамках заданной цели, для которой ММ предназначена, могут быть ослаблены.
При уточнении структуры статической модели руководствуются тем же принципом. Например, если зависимость выхода от входа монотонна, то первым делом пробуют линейную ММ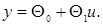 
Если зависимость выхода от входа носит экстремальный характер, то берут квадратичную функцию
а если есть подозрения, что зависимость выхода от входа имеет перегиб, то начинают с кубической функции
Аналогично действует и в случае нескольких входов и выходов. Возможен различный выбор ММ в разных областях переменных. Например, если построение ММ выполняется с целью оптимизации, то вдали от экстремума можно ограничиться линейной моделью, а при приближении к экстремума переходить на квадратичную. В любом случае предпочтительнее модели, в которые постоянные коэффициенты входят линейно.
Если точность моделей с постоянными коэффициентами недостаточна, т.е. исследуемая система нестационарна, то в модель вводят зависимость коэффициентов от времени (дрейф, тренд). Дрейф может быть монотонным или периодическим, причем в большинстве случаев достаточно ограничиться простейшими моделями дрейфа: линейными
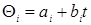
или гармоническими
.
Если возникает дилемма: «выбрать ММ детерминированную или стохастическую», то предпочтение следует отдать детерминированной ММ. И только если не удается обойтись без случайности, то вводят ее, причем сначала в наиболее простой форме, например, приведенной к выходу: 
, где φ -случайное возмущение. Аналогично, переходить к нечеткой ММ следует только при неадекватности стохастических ММ (что в действительности бывает не так уж редко).
Иногда структуру системы характеризуют, кроме прочего, целым числом, определяющим порядок ее динамической модели (например, размерностью вектора состояния ММ, глубиной памяти ММ, максимальной внутренней задержкой и т.п.). В соответствии с принципом простоты, при выборе ММ следует начинать с наименьших значений порядка, учитывая, что многие классы динамических процессов описываются моделями 1-2-го порядка. Например, для описания монотонных (так называемых «апериодических») переходных процессов часто достаточно апериодического звена – линейной стационарной дифференциальной ММ 1-го порядка, имеющей передаточную функцию от входа к выходу
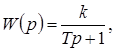
где k – коэффициент усиления статической ММ,
T - постоянная времени звена (Величина Т определяется тем свойством, что за время 3Т переходная составляющая процесса в апериодическом звене уменьшается до 5% от начального уровня).
Для описания колебательных процессов используется колебательное звено – линейное дифференциальное уравнение 2-го порядка, соответствующее передаточной функции
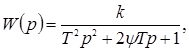
где ψ - показатель затуханий колебаний (| ψ| < 1).
Переходить к ММ более высокого порядка следует лишь тогда, когда экспериментальные данные не позволят принять гипотезу об описании системы моделью данного порядка. Иначе говоря, «не решай сложную задачу, не решив сначала простую».
Отметим, что если ММ системы есть передаточная функция в непрерывном времени, то степень ее числителя не должна превосходить степени знаменателя. Иначе ММ будет включать чистое дифференцирование и ее нельзя будет привести к уравнению состояния. Кроме того, на входные сигналы бесконечной мощности такая ММ будет реагировать сигналами бесконечной мощности, что говорит о ее негрубости. Понятие грубости ММ было введено в конце 20-х годов А.А.Андроновым и означает, что малые изменения исходных данных (входных переменных) приводят к малым изменениям результатов (выходов). Грубость – очень важное свойство модели, так как реальные исходные данные для ее построения и применения всегда содержат ошибки. Если бы эти ошибки существенно сказывались на результатах, моделью просто нельзя было бы пользоваться. Резюмировать сказанное можно в виде принципа грубости: «без ошибки нет модели, а поэтому негрубые модели плохие».
Перечисленные правила следует принимать не как законы, а как рекомендации. В мире моделей царствует плюрализм и для достижения успеха нужно испытать несколько вариантов моделей. При этом самая полная модель не обязательно самая точная, а самая точная не обязательно самая хорошая. Здесь уместно перефразировать слова Э. Хэмингуэя: можно пренебрегать чем угодно, нужно только точно знать, как это повлияет на результат.
Основная литература
1. Царегородцев А.В. Математическое моделирование управляющих систем: Учеб. пособие.— М.: Изд-во РУДН, 2003. — 80 с.
Доцент кафедры Автоматизации
технологических процессов металлургии
и машиностроения
А.В. Манкевич
[1] Счетное множество представляет собой некоторую идеализацию, которую невозможно реализовать практически из-за конечности размеров технических систем и пределов человеческого восприятия. Такие идеализированные модели (например, множество натуральных чисел N ={1, 2,,..}) имеет смысл вводить для множеств конечных, но с заранее не ограниченным (или неизвестным) числом элементов.
[2] Формально понятие операции является частным случаем понятия отношения между элементами множеств. Например, операция сложения двух чисел задает 3-местное (тернарное) отношение R: тройка чисел (х, у, z) принадлежит отношению R, если z = x + y.
[3] Здесь и далее вектор (столбец) с компонентами x 1, x 2, …. xn обозначается
[4] λ – комплексное число, аргумент полиномов А(λ), В(λ).
