Система может быть дискретной или непрерывной по входам, по выходам и по времени в зависимости от того, дискретными или непрерывными являются множества U, Y, Т соответственно. Под дискретным понимается конечное или счетное[1] множество. Под непрерывным будем понимать множество объектов, для которого адекватной моделью служит отрезок, луч или прямая линия, т.е. связное числовое множество. Если система имеет несколько входов и выходов, то это значит, что соответствующие множества U, Т лежат в многомерных пространствах, т.е. непрерывность и дискретность понимаются покомпонентно.
Удобство числового множества как модели реальных совокупностей объектов состоит в том, что на нем естественным образом определяются несколько отношений, формализующих реально встречающиеся отношения между реальными объектами. Например, отношения близости, сходимости формализуют понятия похожести, сходства объектов и могут быть заданы посредством функции расстояния (метрики) d(x, у) (например, d(x, у) = | х - у |). Числовые множества являются упорядоченными: отношение порядка следования (х ≤ у) формализует предпочтение одного объекта другому. Наконец, над элементами числовых множеств определены соответствующие операции[2], например, линейные: х + у, х*у. Если для реальных объектов на входе и выходе также имеют смысл аналогичные операции, то естественным образом возникают требования к моделям (1) – (3): быть согласованными с этими операциями, сохранять их результаты. Таким образом, приходим, например, к линейным моделям: y = au + b, dy/dt = ay + bu и т.д., являющихся простейшими моделями многих процессов.
Как правило, дискретность множества U влечет за собой дискретность Y. Кроме того, для статических систем исчезает различие между непрерывным и дискретным временем. Поэтому классификация детерминированных систем по признакам «статические-динамические», «дискретные-непрерывные» включает шесть основных групп, представленных в таблице 2, где для каждой группы указан математический аппарат описания систем, методы численного анализа и оценки их параметров, методы синтеза (оптимизации), а также типичные области применения.
Таблица 2
ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ СИСТЕМ
| Типы систем | Статические | Динамические | ||||
| Дискретные по U.Y | Непрерывные по U.Y | Дискретные по Т | Непрерывные по Т | |||
| Дискретные по U, Y | Непрерывные по U,Y | Дискретные по U,Y | Непрерывные по U, Y | |||
| Математический аппарат описания | Графы, таблицы соответствий, булева алгебра | Функции вещественных переменных | Конечные автоматы | Разностные уравнения | Асинхронные автоматы, сети Петри, модели теории расписаний | Обыкновенные дифференциальные уравнения |
| Методы оценки параметров и анализа | Методы математической логики | Методы интерполяции и аппроксимации | Теория конечных автоматов | Идентификация, теория устойчивости | Методы идентификации | Идентификация, численное интегрирование ОДУ |
| Методы синтеза | Дискретное программирование, метод Куайна, карты Карно | Методы оптимизации (линейное и нелинейное программирование) | Динамическое программирование, методы синтеза микропрограммных автоматов | Динамическое программирование, дискретный принцип максимума | Динамическое программирование, теория расписаний | Теория управления, методы оптимизации |
| Области применения | Качественные модели исследования операций | Количественные модели исследования операций | Цифровые САУ, ГАП, логическое управление | Импульсные и цифровые САУ | Параллельные процессы в ЭВМ и ГАП | САУ, механические, тепловые, электронные и др. процессы |
Примечание: U - множество входов, Y - множество выходов системы
Модели состояния динамических систем
Модели общего вида
Важнейшую роль при описании динамических систем играет понятие состояния. Состояние - это совокупность величин (вектор)[3] 
, которые определяют (вместе с входным воздействием) будущее поведение системы.
В общем случае уравнения состояния – это системы дифференциальных или разностных уравнений первого порядка вместе с уравнениями для выходных величин. Начальное состояние представляет, «память» системы о прошлом. Модель состояния непрерывной динамической системы записывается в виде
(4)
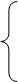
(5)
где u 1, …, um - входные переменные, y 1, …, yl - выходные переменные, x 1, …, xn -переменные состояния. Вводя векторные обозначения, можно записать (5) в более компактном виде:
(6)
где 
, 
, 
.
Для моделей состояния справедлив следующий факт: любая нелинейная динамическая система может быть представлена как соединение линейных динамических и нелинейных статических звеньев.
Еще более общей формой описания динамических систем являются сингулярные дифференциальные (алгебро-дифференциальные) системы
(7)
частным случаем которых являются неявные системы
(8)
Линейные модели
Часто вместо (5) используют упрощенные ММ, основанные на том, что процессы в системе протекают, мало отклоняясь от некоторой так называемой опорной траектории 
удовлетворяющей уравнениям
. (9)
Тогда можно записать приближенную линеаризованную модель в отклонениях от этого режима:
(10)
где 
, 
, 
,
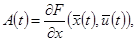
Если расчетный режим является установившимся, т.е. не зависит от времени, то коэффициенты в (10) также не зависят от времени: A(t)=A, B(t)=B и т.д. Такие системы называются стационарными. Особенно часто на практике встречаются стационарные линейные непрерывные системы, описываемые более простыми уравнениями
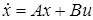, у = Сх. (11)
Матрицы А, В, С являются параметрами модели (11).
Если линеаризация приводит к большим погрешностям, то стараются, по возможности, выбрать ММ линейную по параметрам:
,
где А - матрица параметров порядка n × N,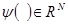 
- нелинейная функция. К этому классу относятся, в частности, билинейные объекты.
Сказанное выше относится и к уравнениям дискретных по времени систем. Уравнения дискретной системы в общем случае имеют вид
, 
. (12)
Дискретным аналогом уравнений линейной стационарной системы (20) являются уравнения:
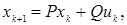
(13)
Наряду с уравнениями состояния широкое применение находят также модели в переменных «вход-выход» и модели, описываемые передаточными функциями. Для непрерывного времени уравнение «вход-выход» имеет вид
A(p)y(t)=B(p)u(t), (14)
где р = d/dt - символ дифференцирования по времени, 
, 
, причем в (14) всегда m < n. Дробно-рациональная функция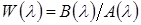 
называется передаточной функцией системы (14), а полином А(λ) - ее характеристическим полиномом [4]. Если уравнение (14) получено из (11), то
(15)
Они справедливы и в случае, когда вход и выход системы (11) являются векторами, при этом 
- матрица. Пользуясь (15), можно показать, что замена переменных состояния в (11) по формуле 
, где Т - неособая n×n матрица (det T = 0), не приводит к изменению передаточной функции (15). Это значит, что обратный переход от описания «вход-выход» к уравнениям состояния (11) неоднозначен: при сохранении передаточной функции базис в пространстве состояний можно выбирать по-разному. На практике применяются несколько типовых способов перехода от передаточной функции к уравнениям состояния. Эти способы соответствуют так называемым каноническим представлениям системы. Опишем один из них, приводящий к управляемому каноническому представлению. Вместо (13) вводятся два уравнения:
, (16-а)
(16-б)
где η - вспомогательная переменная.
Очевидно, что передаточные функции (14) и (16) совпадают. В качестве вектора состояния в уравнении (13) берется 
, так что 
. Из (16-а) и соотношений 
выводится форма матрицы А и вектора В в (11), а из (16-б), записанного в виде 
, получаем строку С:
(17)
Если для системы (14) наблюдению доступна производная 
от величины y при i<n-m -1, То она может быть получена, если в найденных уравнениях сохранить A, B, в форме (17) взять 
Если в (14) m=n (такие передаточные функции называют несобственными), то систему (14) нельзя привести к виду (11), но можно привести к виду
(18)
где А и В имеют вид (17), 
