Исследование движения тел в жидкости
Теоретический минимум
- Идеальная жидкость. Описание движения жидкости с помощью метода Эйлера. Уравнение неразрывности. Уравнение Бернулли.
- Вязкость жидкости. Закон Ньютона. Физический смысл величин, входящих в закон Ньютона. Кинематическая и динамическая вязкость.
- Метод Стокса, использующийся для определения коэффициента внутреннего трения.
- Ламинарное и турбулентное движение жидкости. Расход жидкости. Формула Пуазейля. Число Рейнольдса.
Контрольные задания
Вариант 1
1. Показать, что при установившемся течении идеальной жидкости для любой трубки тока выполняется уравнение неразрывности.
 2. Найти скорость течения воды в трубе АВ, если разность уровней в трубках а и в равна 10 см.
2. Найти скорость течения воды в трубе АВ, если разность уровней в трубках а и в равна 10 см.
3. Какой наибольшей скорости может достичь дождевая капля диаметром  мм, если динамическая вязкость воздуха
мм, если динамическая вязкость воздуха 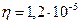 Па.с?
Па.с?
4. В трубе с внутренним диаметром 3 см течет вода (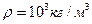 ,
,  ,
,  ). Определить максимальный массовый расход воды при ламинарном течении.
). Определить максимальный массовый расход воды при ламинарном течении.
5. В сосуд льется вода, причем за единицу времени наливается объем воды 0,2 л/с. Каким должен быть диаметр отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h=10 см?
Вариант 2
1. На чем основан вывод уравнения Бернулли и каков физический смысл его составляющих?
 2. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы равна 20 см/с. Чему равна скорость в узкой части трубы, если ее диаметр в 1,5 раза меньше?
2. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы равна 20 см/с. Чему равна скорость в узкой части трубы, если ее диаметр в 1,5 раза меньше?
3. Найти разность уровней в трубках а и в, если скорость течения жидкости в трубе равна 1м/с.
4. Медный шарик диаметром d=1см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? турбулентным? 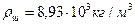 ,
,  ,
,  ,
,  .
.
5. Бак высотой h1=1,5м наполнен до краев водой. На расстоянии h2=1,0м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии от бака падает на пол струя, вытекающая из отверстия?
Вариант 3
1. Чем обусловлена вязкость в жидкости? Почему с повышением температуры вязкость жидкости уменьшается?
2. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы, имеющей диаметр d1, равна  , а в узкой с диаметром d2 равна
, а в узкой с диаметром d2 равна  . Чему равно отношение
. Чему равно отношение 
 , если отношение
, если отношение  ?
?
3. Пробковый шарик (ρп=240 кг/м3) радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом ( ). Найти динамическую и кинематическую вязкость касторового масла, если шарик всплывает с постоянной скоростью 3,5 см/с.
). Найти динамическую и кинематическую вязкость касторового масла, если шарик всплывает с постоянной скоростью 3,5 см/с.
4. Вода течет по круглой трубе диаметром 5 см со средней скоростью 10 см/с. Определить число Рейнольдса для потока жидкости в трубе и указать характер течения жидкости.
5. Горизонтальный цилиндр насоса имеет диаметр 20 см. В нем движется со скоростью 1 м/с поршень, выталкивающий воду через отверстие диаметром 2 см. С какой скоростью будет вытекать вода из отверстия?
Вариант 4
1. Чем обусловлена вязкость в газе? Почему с повышением температуры вязкость газов увеличивается?
2. Динамическая вязкость некоторой жидкости  . С какой скоростью будет падать свинцовая дробинка диаметром 1мм в сосуде, наполненном этой жидкостью?
. С какой скоростью будет падать свинцовая дробинка диаметром 1мм в сосуде, наполненном этой жидкостью?
3. Бак цилиндрической формы площадью основания 10 м2 и объемом 100 м3 заполнен водой. Пренебрегая вязкостью воды, определить время, необходимое для полного опустошения бака, если на дне бака образовалось отверстие площадью 8 см2.
4. В широкой части горизонтально расположенной трубы нефть течет со скоростью 2 м/с ( ). Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях ее равна 6,65 кПа.
). Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях ее равна 6,65 кПа.
5. При движении шарика радиусом 2,4 мм в касторовом масле ( ) ламинарное обтекание наблюдается при скорости, не превышающей 10 см/с. При какой минимальной скорости шарика радиусом 1 мм в глицерине обтекание станет турбулентным (
) ламинарное обтекание наблюдается при скорости, не превышающей 10 см/с. При какой минимальной скорости шарика радиусом 1 мм в глицерине обтекание станет турбулентным (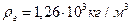 )?
)?
Вариант 5
1. Поясните формулу Пуазейля. Как с помощью данной формулы можно определить коэффициент вязкости жидкости?
2. Определить плотность газа, протекающего по трубе, если известно, что за время 10 мин через поперечное сечение трубы, равное 4 см2, протекает газ массой 480г.
3. В сосуд заливается вода со скоростью 0,5 л/с. Определить диаметр отверстия в сосуде, при котором вода поддерживалась бы в нем на постоянном уровне h=20 см.
4. Латунный шарик диаметром 0,5 мм падает в глицерине. Определить скорость установившегося движения шарика.
5. По трубе течет машинное масло ( ,
,  ). Максимальная скорость, при которой движение масла в этой трубе остается еще ламинарным, равна 3,2 см/с. При какой скорости движение глицерина (
). Максимальная скорость, при которой движение масла в этой трубе остается еще ламинарным, равна 3,2 см/с. При какой скорости движение глицерина (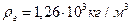 ) в той же трубе переходит из ламинарного в турбулентное?
) в той же трубе переходит из ламинарного в турбулентное?
Лабораторные работы
№ 1.11. Исследование законов колебательного движения физического маятника и определение ускорения свободного падения
№ 1.12. Определение ускорения свободного падения с помощью математического и оборотного маятников
№ 1.13. Определение приведенной длины физического маятника и ускорения свободного падения
№ 1.14. Изучение резонансных явлений при колебаниях плоской пружины
Теоретический минимум
- Гармонические колебания и их характеристики.
- Дифференциальное уравнение гармонических колебаний и его решение.
- Гармонический осциллятор. Пружинный, физический и математический маятники. Приведённая длина физического маятника.
- Сложение одинаково направленных и взаимно перпендикулярных колебаний.
- Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Логарифмический декремент затуханий, добротность.
- Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
Контрольные задания
Вариант 1
1. Уравнение гармонических колебаний точки
 .
.
Каков период этих колебаний?
2. Уравнение колебаний материальной точки массой  г имеет вид
г имеет вид
 см.
см.
Найти максимальную силу, действующую на точку.
3. Однородный диск радиусом R совершает колебания около горизонтальной оси, проходящей на расстоянии R/2 от центра диска. Чему равна циклическая частота колебаний диска?
4. Материальная точка участвует в двух взаимно перпендикулярных колебаниях согласно уравнениям
 и
и  .
.
Какова траектория результирующего движения точки?
5. Амплитуда затухающих колебаний уменьшилась в е раз за 50 колебаний. Каков логарифмический декремент затухания?
6. Период Т0 собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период Т того же маятника стал равным 0,56 с. Какова резонансная частота колебаний?
Вариант 2
1. Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимального значения?
2. Найти отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для момента, когда смещение точки от положения равновесия 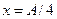 .
.
3. Обруч радиуса R совершает малые колебания относительно оси, проходящей через его край. Каков период этих колебаний?
4. Складываются два взаимно перпендикулярных колебания с одинаковыми частотами. При какой разности фаз результирующее колебание будет линейным?
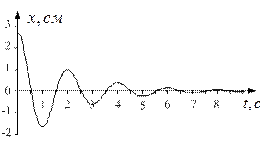
5. Затухающие колебания описываются уравнением
 .
.
График колебания представлен на рисунке. Определите время релаксации.
6. Уравнение движения системы имеет вид
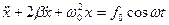 .
.
Чему равен период установившихся вынужденных колебаний системы?
Вариант 3
1. Скорость материальной точки, совершающей гармонические колебания, задается уравнением
 .
.
Записать зависимость смещения этой точки от времени.
2. За какое время тело, совершающее колебание с периодом Т, проходит первую половину пути от среднего значения до крайнего?
3. Однородный стержень длиной  совершает малые колебания относительно оси, проходящей через его край. Какова частота этих колебаний?
совершает малые колебания относительно оси, проходящей через его край. Какова частота этих колебаний?
4. Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Чему равна разность фаз складываемых колебаний?
5. Начальная амплитуда колебания маятника А0=3см. Через t1=10c она равна А1=1см. Через какой промежуток времени она станет равной А2=0,3см?
6. Изобразить резонансные кривые А(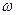 ) для трех коэффициентов затухания
) для трех коэффициентов затухания  .
.
Вариант 4
1. Уравнение движения точки
 см.
см.
Найти период колебаний, максимальную скорость и максимальное ускорение точки.
2. Найти отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для момента времени t=T/6.
3. Однородный диск радиусом R подвешен за край. Чему равна частота его малых колебаний?
4. Точка участвует в двух одинаково направленных колебаниях, данных уравнениями
 см и
см и  см.
см.
Начертить векторную диаграмму сложения амплитуд. Найти амплитуду и начальную фазу результирующего колебания.
5. Логарифмический декремент затухания математического маятника  . Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
6. Чему равна резонансная амплитуда Арез = А(ωрез) у системы без трения?
Вариант 5
1. Колебания материальной точки совершаются по закону
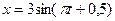 см.
см.
Определить наибольшие значения скорости и ускорения.
2. Груз массой m осторожно прикрепляют к концу свободно висящей пружины. Когда груз освобождают, он опускается на 30см, а затем начинает колебаться. Чему равна частота колебаний?
3. Физический маятник представляет собой тонкий однородный стержень длиной  и массой m с укрепленным на его конце маленьким шариком массой m. Маятник совершает колебания относительно горизонтальной оси, проходящей через центр стержня. Каков период гармонических колебаний маятника?
и массой m с укрепленным на его конце маленьким шариком массой m. Маятник совершает колебания относительно горизонтальной оси, проходящей через центр стержня. Каков период гармонических колебаний маятника?
4. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями
 и
и  , где А1=2см, А2=1см.
, где А1=2см, А2=1см.
Найти уравнение траектории точки.
5. Амплитуда затухающих колебаний маятника за 5 минут уменьшилась в два раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь раз?
6. Найти приближенное значение Арез при  .
.
Лабораторные работы
№ 1.15а. Определение скорости звука в воздухе методом стоячей волны
№ 1.15б. Определение скорости звука в воздухе методом сдвига фаз
Теоретический минимум
- Распространение волн в упругой среде. Продольные и поперечные волны. Скорость волны.
- Уравнение плоской и сферической волны. Длина волны. Волновое уравнение.
- Интерференция волн. Стоячие волны.
- Энергия волны. Вектор Умова.
- Эффект Доплера.
Контрольные задания
Вариант 1
1. Задано уравнение плоской волны
 .
.
Определить частоту, длину волны и фазовую скорость.
2. Волна распространяется в упругой среде со скоростью  м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту колебаний.
м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту колебаний.
3. Найти скорость распространения продольных упругих колебаний в меди.
4. Определить длину бегущей волны, если в стоячей волне расстояние между первой и седьмой пучностями равно 15 см.
Вариант 2
1. Изменение давления в звуковой волне дается выражением
 ,
,
где р измеряется в паскалях, x – в метрах, а t в секундах.
Определить длину волны, частоту и скорость распространения.
2. Найти разность фаз колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 2м, если длина волны  м.
м.
3. Найти скорость распространения звука в стали.
4. Определить длину бегущей волны, если в стоячей волне расстояние между первым и четвертым узлом равно 15см.
Вариант 3
1. Уравнение плоской волны имеет вид
 .
.
Определить частоту, длину волны и фазовую скорость.
2. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии  см, в момент времени
см, в момент времени  равно половине амплитуды. Найти длину бегущей волны.
равно половине амплитуды. Найти длину бегущей волны.
3. Найти скорость распространения поперечных упругих колебаний в меди.
4. В трубе длиной 1,2м находится воздух. Определить минимальную частоту возможных колебаний воздушного столба в двух случаях: 1) труба открыта; 2) труба закрыта. Скорость звука принять равной 340 м/с.
Вариант 4
1. Уравнение плоской волны имеет вид
 .
.
Определить частоту, длину волны и фазовую скорость.
2. Две точки находятся на расстоянии 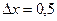 м друг от друга на прямой, вдоль которой распространяется волна со скоростью
м друг от друга на прямой, вдоль которой распространяется волна со скоростью  м/с. Период колебаний равен 0,05с. Какова разность фаз колебаний в этих точках?
м/с. Период колебаний равен 0,05с. Какова разность фаз колебаний в этих точках?
3. Определить скорость звука в азоте при температуре Т=300К.
4. Один из способов измерения скорости звука в воздухе состоит в следующем. В широкой трубке может перемещаться поршень, а перед ее открытым концом расположен звучащий камертон. Отодвигая поршень от конца трубки, наблюдатель отмечает следующих друг за другом увеличения и уменьшения громкости звука. Найти скорость звука в воздухе, если при частоте колебаний 440 Гц двум последовательным усилениям интенсивности звука соответствует расстояние между положениями поршня, равное 0,375м.
Вариант 5
1. Плоская звуковая волна возбуждается источником колебаний частоты ν=200Гц. Амплитуда колебаний источника равна 4 мм. Написать уравнение плоской волны, если в начальный момент смещение точек источника максимально. Скорость звуковой волны принять равной 300м/с.
2. Какова скорость распространения волны в упругой среде, если разность фаз колебаний двух точек среды, отстоящих дуг от друга на расстояние 10см, равна π/3. Частота колебаний 25Гц.
3. Найти положение узлов и пучностей и начертить график стоячей волны, если: а) отражение происходит от менее плотной среды; б) отражение происходит от более плотной среды. Длина бегущей волны 6см.
4. Найти отношение скоростей звука в водороде и углекислом газе при одинаковой температуре газов.
Лабораторные работы
№ 1.16 Определение коэффициента внутреннего трения воздуха при различных температурах
№ 1.20 Изучение реального газа (Эффект Джоуля-Томсона)
Теоретический минимум
- Уравнение Клайперона-Менделеева. Основное уравнение молекулярно-кинетической теории газов.
- Барометрическая формула. Распределение Больцмана.
- Максвелловское распределение молекул по скоростям.
- Эффективный диаметр и средняя длина свободного пробега молекул.
- Явления переноса. Вязкость газов. Диффузия. Теплопроводность. Механизм вязкости газов. Зависимость вязкости газов от температуры. Формула Пуазейля и ее применение для определения вязкости газов.
- Реальные газы. Силы межмолекулярного взаимодействия.
- Поправки Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса.
Контрольные задания
Вариант 1
1. Явление диффузии. Закон Фика. Физический смысл коэффициента диффузии.
2. Чему равна плотность ρ азота, находящегося в баллоне под давлением р = 2 МПа при температуре Т = 400 К?
3. При повышении температуры в 1,5 раза происходит диссоциация молекул двухатомного газа. Как при этом изменяется давление газа?
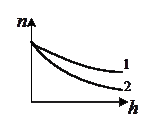 4. На рисунке приведены зависимости концентрации частиц некоторого газа от высоты. Какая кривая соответствует большей температуре газа?
4. На рисунке приведены зависимости концентрации частиц некоторого газа от высоты. Какая кривая соответствует большей температуре газа?
5. Средняя длина свободного пробега молекул определяется выражениями
a) 1/<z> б) < υ>/<z> в)  ·
·  г)
г)  πd2n< υ>
πd2n< υ>
1) а, б 2) б, в. 3) в, г 4) а,г
6. Теплопроводность в газах обусловлена
1) силами межмолекулярного взаимодействия;
2) переносом импульса упорядоченного движения молекул;
3) переносом энергии молекул;
4) переносом массы молекул из одного слоя в другой.
7. Ван-дер-Ваальсом были введены в уравнение Клайперона-Менделеева поправки, учитывающие
1) собственный объем молекул, скорость движения молекул;
2) собственный объем молекул, притяжение молекул;
3) скорость движения молекул, притяжение молекул;
4) скорость движения молекул, колебательные степени свободы.
Вариант 2
1. Явление теплопроводности. Закон Фурье. Физический смысл коэффициента теплопроводности.
2. Газ при температуре Т = 309 К и давлении р = 0,7 МПа имеет плотность ρ = 12 кг/м3. Чему равна молярная масса газа?
3. В результате уменьшения объема газа в 3 раза и увеличения средней кинетической энергии его молекул в 2 раза давление газа
1) не изменилось 2) увеличилось в 2 раза
3) увеличилось в 3 раза 4) увеличилось в 6 раз
4. Найти отношение давления воздуха на высоте h 2 к давлению воздуха на высоте h 1 при постоянной температуре Т.
5. По какой формуле можно найти среднее число столкновения молекул?
1) 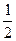 π d 2 n 2)
π d 2 n 2)  3)
3)  π d 2 n < υ> 4)
π d 2 n < υ> 4) 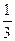 < υ>< λ>
< υ>< λ>
6. Явления переноса характеризуются коэффициентом вязкости (а), коэффициентом диффузии (б), коэффициентом теплопроводности (в). Какой из этих коэффициентов не зависит от плотности газа?
7. Если уменьшение объема насыщенного пара происходит при постоянной температуре, то его давление
1) увеличится; 2) останется прежним; 3) уменьшится;
Вариант 3
1. Явление внутреннего трения. Закон Ньютона. Физический смысл коэффициента вязкости.
2. В сосуде емкостью V = 5 л находится кислород, концентрация п молекул которого равна 9,41·1023 м-3. Чему равна масса т газа?
3. Два идеальных газа характеризуются следующими параметрами: р1, ρ1 и р2 = 2р1, ρ2 = ρ1/2. Чему равно отношение значений среднеквадратичных скоростей движения их молекул υ2/ υ1?
4. Найти высоту, на которой давление газа равно 0,8 давления на уровне моря, считая, что температура Т не меняется.
5. По какой формуле можно найти среднюю длину пробега молекул?
1)  2)
2) 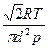 3)
3)  4)
4) 
 6. Температура газовой системы изменяется согласно графику. Сравните плотности потока энергии, переносимой в направлении оси Оx через одинаковые сечения I и II.
6. Температура газовой системы изменяется согласно графику. Сравните плотности потока энергии, переносимой в направлении оси Оx через одинаковые сечения I и II.
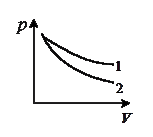
 7. На рисунке представлена изотерма реального газа. Состоянию равновесия между жидкостью и паром соответствует участок
7. На рисунке представлена изотерма реального газа. Состоянию равновесия между жидкостью и паром соответствует участок
1) а, в 2) а 3) б 4) в
Вариант 4
1. Основное уравнение молекулярно-кинетической теории идеального газа.
2. В одинаковых баллонах при одинаковой температуре находятся равные массы водорода Н2 и углекислого газа СО2. Во сколько раз давление, производимое водородом больше?
3. Давление идеального газа 2 мПа, концентрация молекул 2·1010 см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы этого газа.
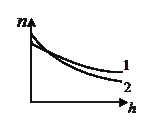 4. На рисунке приведены зависимости концентрации частиц двух разных газов от высоты. Какая кривая соответствует более легким молекулам?
4. На рисунке приведены зависимости концентрации частиц двух разных газов от высоты. Какая кривая соответствует более легким молекулам?
5. В результате протекания изотермического процесса давление газа увеличилось в k раз. Как при этом изменилась длина свободного пробега?
6. Внутреннее трение в газах обусловлено:
1) силами межмолекулярного взаимодействия;
2) переносом импульса упорядоченного движения молекул;
3) переносом энергии молекул;
4) переносом массы молекул из одного слоя в другой.
7. Учет сил притяжения между молекулами газа приводит к появлению внутреннего давления на газ, которое равно
1)  2)
2)  3)
3)  4)
4) 
Вариант 5
1. Уравнение Клапейрона-Менделеева. Изопроцессы.
2. При увеличении абсолютной температуры идеального газа в 2 раза давление газа увеличилось на 25 %. Во сколько раз при этом изменился объем?
3. Давление газа на стенки сосуда
1) пропорционально υ; 2) пропорционально υ1/2;
3) не зависит от υ; 4) пропорционально υ2,.
где υ – средняя квадратичная скорость молекулы.
4. Найти высоту, на которой плотность воздуха в е раз меньше плотности воздуха на уровне моря, считая температуру неизменной.
5. Найти зависимость среднего числа столкновений <z> молекулы идеального газа за 1 с от давления р при изохорном процессе.
6. Определить зависимость динамической вязкости от Т при изобарном процессе.
7. Внутренняя энергия моля реального газа (с учетом потенциальной энергии межмолекулярного взаимодействия) отличается от внутренней энергии идеального газа на величину
1)  2)
2)  3)
3)  4)
4) 
Вариант 6
1. Распределение Больцмана. Влияние температуры и массы молекул на характер распределения.
2. При увеличении объема газа в 2 раза давление увеличилось на 120 кПа, а абсолютная температура возросла на 10 %. Каким было первоначальное давление?
3. Во сколько раз средняя квадратичная скорость молекул кислорода меньше средней квадратичной скорости молекул водорода, если температуры газов одинаковы?
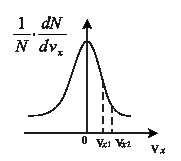 4. На рисунке представлен график функции распределения молекул по проекциям скорости υх. Числа молекул, имеющих проекции в интервалах: от 0 до υх1(N 1) и от υх1 до υх2(N 2) соотносятся как
4. На рисунке представлен график функции распределения молекул по проекциям скорости υх. Числа молекул, имеющих проекции в интервалах: от 0 до υх1(N 1) и от υх1 до υх2(N 2) соотносятся как
1) N 1 > N 2.
2) N 2 > N 1
3) N 1 = N 2
4) зависимость не дает информации о количестве молекул
5. Найти зависимость средней длины свободного пробега молекул идеального газа от температуры Т при изобарном процессе.
6. Определить зависимость динамической вязкости h от температуры Т при изохорном процессе.
 7. На рисунке представлена изотерма реального газа. Насыщенному пару соответствуют области
7. На рисунке представлена изотерма реального газа. Насыщенному пару соответствуют области
1) а 2) б
3) в 4) а, в
Вариант 7
1. Максвелловское распределение молекул по скоростям. Наиболее вероятная, средняя и средняя квадратичная скорости.
2. При нагревании газа на 1 К при постоянном объеме его давление увеличилось на 0,2 %. Какова начальная температура газа?
3. Давление идеального газа выражается формулами
а) p = nkT б)  в)
в) 
г)  ρ υкв2 д)
ρ υкв2 д) 
1) а, б 2) а, б, г 3) а, в, г, д 4) а, б, в, г, д
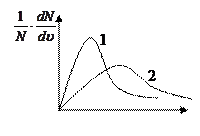 4. Представленным кривым распределения Максвелла соответствуют параметры
4. Представленным кривым распределения Максвелла соответствуют параметры
1) Т 1 = Т 2, М 1 > М 2
2) Т 1 = Т 2, М 2 > М 1.
3) М 1 = М 2, Т 1 > Т 2
4) М 1 = М 2, Т 2 > Т 1
5. Найти зависимость средней длины свободного пробега молекул идеального газа от давления р при изотермическом процессе.
 6. Концентрация молекул газа вдоль оси х изменяется согласно графику. Сравните перенос массы вещества в горизонтальном направлении через одинаковые сечения I и II.
6. Концентрация молекул газа вдоль оси х изменяется согласно графику. Сравните перенос массы вещества в горизонтальном направлении через одинаковые сечения I и II.
7. Удельная теплоемкость твердых тел, с учетом закона Дюлонга и Пти, равна
1)  2)
2) 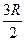 3) 3 R 4)
3) 3 R 4) 
Вариант 8
1. Вывод формулы для расчета длины свободного пробега молекул.
2. В баллоне вместимостью V = 5 л находится азот массой т = 17,5 г. Чему равна концентрация п молекул азота в баллоне?
3. При неизменной концентрации молекул идеального газа в результате нагревания давление газа увеличилось в 4 раза. Как при этом изменилась средняя квадратичная скорость теплового движения молекул?
4. Площадь под кривой распределения молекул по скоростям
1) увеличивается при увеличении температуры
2) увеличивается при уменьшении давления
3) зависит от Т и р
4) остается постоянной.
5. Найти зависимость среднего числа столкновений <z> молекулы идеального газа за 1 с от давления р при изотермическом процессе.
6. Явление диффузии обусловлено:
1) силами межмолекулярного взаимодействия
2) переносом импульса упорядоченного движения молекул
3) переносом энергии молекул
4) переносом массы молекул из одного слоя в другой.
7. Внутренняя энергия моля реального газа равна
1)  2) С v T 3)
2) С v T 3) 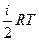 4)
4) 
Лабораторные работы
№ 1.17. Определение удельной теплоемкости воздуха при постоянном давлении
№ 1.18. Определение отношения теплоемкости возду-ха при постоянном давлении и постоянном объеме
№ 1.19. Определение удельной теплоты кристалл-лизации и изменения энтропии при охлаждении олова
Теоретический минимум
- Термодинамическая система и её параметры.
- Число степеней свободы молекул. Закон равномерного распределения энергии по степеням свободы.
- Внутренняя энергия и теплоёмкость идеального газа. Недостаточность классической теории теплоемкости.
- Работа в термодинамике.
- Первое начало термодинамики и её применение к изопроцессам.
- Уравнение адиабаты.
- Фазы и фазовые переходы 1 и 2 рода.
- Уравнение Клапейрона-Клаузиуса.
- Диаграмма состояния. Тройная точка.
- Энтропия системы. Закон возрастания энтропии.
- Энтропия идеального газа.
Контрольные задания
Вариант 1
1. Вывести уравнение Майера.
 2. Внутренняя энергия некоторого газа 60 МДж. На долю поступательного движения приходится 36 МДж. Определить количество атомов в молекуле.
2. Внутренняя энергия некоторого газа 60 МДж. На долю поступательного движения приходится 36 МДж. Определить количество атомов в молекуле.
3. Какова работа, выполняемая идеальным газом за один цикл, представленный на рисунке.?
4. Какая часть количества теплоты, сообщенной одно-атомному газу в изобарном процессе, идет на увеличение внутренней энергии?
5. Вычислить показатель адиабаты двухатомного идеального газа.
6. Плотность некоторого двухатомного газа при нормальных условиях ρ = 1,43 кг/м3. Найти удельную теплоемкость газа при постоянном объеме.
 7. При прямом цикле Карно тепловая машина совершает работу 200 Дж. Температура нагревателя 375 оС, холодильника 300 оС. Определить количество теплоты, получаемое от нагревателя.
7. При прямом цикле Карно тепловая машина совершает работу 200 Дж. Температура нагревателя 375 оС, холодильника 300 оС. Определить количество теплоты, получаемое от нагревателя.
8. Для замкнутого цикла, представленного на рисунке, энтропия газа возрастает на стадии
1) 1-2 2) 2-3
3) 1-2, 2-3 4) 2-3, 3-1
Вариант 2
1. Вывести уравнение Пуассона.
2. Найти отношение средней кинетической энергии вращательного движения молекул к их внутренней энергии для 3-х атомных молекул газа.
 3. Чему равна работа, выполненная идеальным газом за один цикл, представленный на рисунке?
3. Чему равна работа, выполненная идеальным газом за один цикл, представленный на рисунке?
4. В процессе изохорного нагревания водорода объемом V его давление изменилось на Δ р. Какое количество теплоты сообщено газу?
5. Вычислить показатель адиабаты для трехатомного газа.
6. Чему равна теплоемкость водорода при постоянном объеме?
7. При прямом цикле Карно тепловая машина совершает работу 200 Дж. Температура нагревателя 375 оС, холодильника 300 оС. Определить количество теплоты, получаемое от нагревателя.
8. Изменение энтропии при изохорном нагреве моля вещества от температуры Т 1 до температуры Т 2 равно
1)  2) С v(Т 2 – Т 1) 3) (Т 2 – Т 1) 4)
2) С v(Т 2 – Т 1) 3) (Т 2 – Т 1) 4) 
Вариант 3
1. Вывести формулу работы газа при изотермическом процессе.
2. Найти отношение средней кинетической энергии поступательного движения молекул газа к внутренней энергии газа, выраженное через число степеней свободы молекулы.
 3. Чему равна работа, совершаемая одним молем идеального газа за цикл, представленный на рисунке?
3. Чему равна работа, совершаемая одним молем идеального газа за цикл, представленный на рисунке?
4. Какая часть количества теплоты, сообщенной двухатомному газу в изобарном процессе, идет на увеличение внутренней энергии?
5. Вычислить показатель адиабаты для одноатомного газа.
6. Плотность некоторого двухатомного газа при нормальных условиях ρ = 1,43 кг/м3. Найти его удельную теплоемкость при постоянном давлении.
7. Газ в цикле Карно с коэффициентом полезного действия 0,8 совершил работу 38,4 кДж. Какое количество теплоты передано газу нагревателем?
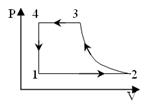 8. Энтропия газа уменьшается при протекании следующих процессов
8. Энтропия газа уменьшается при протекании следующих процессов
1) 1-2, 2-3 2) 3-4, 4-1
3) 3-4, 2-3 4) 4-1, 1-2, 2-3
Вариант 4
1. Вывести формулу работы идеального газа при адиабатном процессе.
2. Из скольких атомов состоит молекула газа, если средние энергии поступательного и вращательного движения молекул одинаковы?
3. Объем идеального газа увеличивается от одного и того же объема и давления: а) изотермически, б) изобарически, в) по закону p ~ V -2. При этом верным соотношением между работами газа в ходе одинакового изменения объема является
1) А б> А а> А в 2) А а > А б> А в 3) А б> А в > А а 4) А в > А б> А а
4. Работа расширения некоторого одноатомного идеального газа при изобарном процессе составляет 2 кДж. Чему равно количество подведенной к газу теплоты?
5. Формулы для расчета показателя адиабаты
а) 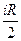 б)
б)  в)
в)  г)
г)  д)
д) 
1) а, б 2) в, д 3) а, д 4) б, д
6. На нагревание некоторого количества вещества массой 0,2 кг от температуры 12 оС до 16,4 оС потребовалось 300 Дж теплоты. Оценить удельную теплоемкость вещества.
 7. Идеальная тепловая машина в течение цикла получает от нагревателя количество теплоты 2095 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Чему равна работа машины за один цикл?
7. Идеальная тепловая машина в течение цикла получает от нагревателя количество теплоты 2095 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Чему равна работа машины за один цикл?
8. Для замкнутого цикла, представленного на рисунке, энтропия уменьшается при протекании следующих процессов:
1) II 2) II, III 3) III, IV 4) IV, I
Вариант 5
1. Вывести формулу КПД цикла Карно.
2. Найти внутреннюю энергию двухатомного газа, если на долю вращательного движения приходится энергия 22 МДж.
 3. Газ переходит из состояния 1 в состояние 3 по пути 1-2-3 и 1-4-3. При этом справедливо утверждение
3. Газ переходит из состояния 1 в состояние 3 по пути 1-2-3 и 1-4-3. При этом справедливо утверждение
1) А 123 = А 143
2) А 123 > А 143
3) А 123 < А 143
4) для определения работы газа информации недостаточно.
4. При изобарном нагревании одного моля идеального одноатомного газа было сообщено количество теплоты 5 кДж. Найти изменение внутренней энергии газа.
 5. На рисунке изображены адиабаты двух газов: водорода и аргона. Какой график соответствует аргону?
5. На рисунке изображены адиабаты двух газов: водорода и аргона. Какой график соответствует аргону?
6. Теплоемкость некоторой массы газа при постоянном объеме вычисляется по формуле
1) 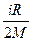 2)
2) 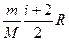 3)
3)  4)
4) 
7. Идеальный газ совершил цикл Карно. Температура нагревателя Т 1 в 3 раза выше температуры Т 2 холодильника. Нагреватель передал газу количество теплоты Q 1 = 42 кДж. Какую работу совершил газ?
8. При изохорном нагревании одноатомного идеального газа (v = 3 моль) его термодинамическая температура увеличилась в п = 2 раза. Найти изменение энтропии при этом процессе.
Вариант 6
1. Записать I закон термодинамики для всех изопроцессов.
2. Отношение средней кинетической энергии вращательного движения молекул газа к средней кинетической энергии поступательного движения, выраженное через число степеней свободы молекулы, равно
1)  2)
2) 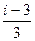 3)
3)  4)
4) 
3. Сравнить работы, которые совершают одинаковые массы водорода и кислорода при изобарном нагревании на одну и ту же температуру.
 4. Двухатомный идеальный газ (v = 2 моль) нагревают при постоянном объеме до Т = 289 К. Найти количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в 3 раза.
4. Двухатомный идеальный газ (v = 2 моль) нагревают при постоянном объеме до Т = 289 К. Найти количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в 3 раза.
5. На рисунке изображены адиабаты двух газов: водорода и аргона. Какой график соответствует водороду?
6. Чему равна удельная теплоемкость кислорода при постоянном давлении?
7. Идеальный газ совершает цикл Карно. Температура Т 1 нагревателя в 4 раза выше температуры Т 2 охладителя. Какую долю количества теплоты, получаемого за один цикл от нагревателя, газ отдает охладителю?
8. Кислород массой т = 2 кг, расширяясь изотермически, увеличил свой объем в 5 раз. Найти изменение энтропии.
Вариант 7
1. Принцип действия и вывод КПД тепловой машины.
2. Из скольких атомов состоит молекула газа, если на долю поступательного движения молекулы приходится энергия 33·10-21 Дж. Полная энергия молекулы 55·10-21 Дж.
3. Найти работу изобарного расширения моля идеального газа при нагревании на 1 К.
4. В процессе изохорного нагревания кислорода объемом V = 20 л его давление изменилось на Δ р = 100 кПа. Какое количество теплоты сообщено газу?
 5. Определить показатель адиабаты γ частично диссоциировавшего газообразного азота, степень диссоциации которого равна 0,4.
5. Определить показатель адиабаты γ частично диссоциировавшего газообразного азота, степень диссоциации которого равна 0,4.
6. Удельная теплоемкость идеального газа при постоянном давлении вычисляется по формуле
1)  2)
2)  3)
3)  4)
4) 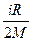
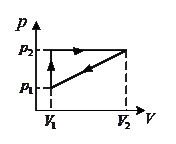
7. Определить КПД цикла, представленного на рисунке, рабочим телом которого является одноатомный идеальный газ, если р 2 = 2 р 1, V 2 = 4 V 1.
8. В результате изохорного нагревания водорода массой т = 1 г давление газа увеличилось в 2 раза. Определить изменение энтропии.
Вариант 8
1. Вывести уравнение адиабаты.
2. Определить среднее значение полной кинетической энергии одной молекулы водяного пара при температуре 400 К.
3. Работы при изотермическом расширении газа от а) 1 до 2 м3 и б) от 2 до 4 м3 соотносятся:
1) А а > А б 2) А а < А б 3) А а = А б 4) А б = 2 А а
4. Какая часть количества теплоты, сообщенной одноатомному газу в изобарном процессе, идет на совершение работы?
5. Уравнение Пуассона представлено формулами
а) pV γ = const б) TV γ-1 = const в) T γ p 1-γ = const г) T γ-1 p γ = const
1) а,б 2) в,г 3) а 4) б
6. Удельная теплоемкость при постоянном объеме некоторого одноатомного газа равна 3,12 Дж/кг·К. Определить молярную массу газа.
 7. Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты Q 1, полученного от нагревателя, отдает холодильнику. Температура Т 2 холодильника равна 280 К. Определить температуру Т 1 нагревателя.
7. Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты Q 1, полученного от нагревателя, отдает холодильнику. Температура Т 2 холодильника равна 280 К. Определить температуру Т 1 нагревателя.
8. В теплую воду бросили лед, он начал таять. Изменению энтропии системы “лед - вода” в процессе установления термодинамического равновесия на графике соответствует зависимость
1) 1 2) 2 3) 3
4) ни одна не соответствует
Вариант 9
1. Вывести уравнение Майера.
2. Определить среднее значение полной кинетической энергии молекулы азота при температуре 1000 К.
3. Работа газа при изотермическом процессе находится по формуле
1) p (V 2 – V 1) 2)  3)
3)  4)
4) 
4. Какая часть количества теплоты, сообщенной двух-атомному газу, идет на совершение работы?
5. Вычислить показатель адиабаты для трехатомного газа.
6. Определить удельную теплоемкость углекислого газа (СО2) при постоянном объеме.
7. Определить КПД цикла Карно, если в результате кругового процесса газ совершил работу А = 1 Дж и передал охладителю количество теплоты Q 2 = 4,2 Дж.
 8. Энтропия газа убывает при протекании следующих процессов
8. Энтропия газа убывает при протекании следующих процессов
1) 1-2, 2-3 2) 2-3, 3-4
3) 3-4, 4-1 4) 4-1, 1-2
Вариант 10
1. Вывести формулу работы газа при адиабатном процессе.
2. Из скольких атомов состоит молекула, если на долю вращательного движения молекулы приходится энергия 11·10-21 Дж, а полная энергия движения молекул равна 22·10-21 Дж?
3. Газ расширяется от объема V 1 до объема V 2: а) изобарно; б) адиабатно; в) изотермически. В каком процессе газ совершает наименьшую работу?
4. В результате изобарного процесса внутренняя энергия трехатомного газа изменилась на 24 МДж. Найти работу, совершенную газом.
5. Вычислить показатель адиабаты для многоатомного газа.
6. Как изменится удельная теплоемкость сv двухатомного газа при полной диссоциации его молекул?
7. Идеальный газ совершает цикл Карно. Работа изотермического расширения А1 = 5 Дж. Определить работу изотермического сжатия А2, если КПД цикла равен 0,2.
8. Одинаковое количество одноатомного и двухатомного газа, нагревают в закрытом сосуде. Начальные и конечные температуры газов в обоих случаях одинаковы. Приращение энтропии во втором случае больше, чем в первом в
1) 2 раза 2) 2,5 раза 3) 3,5 раза 4) 4 раза
Библиографический список
1. Трофимова Т.И. Курс физики: учебн. пособие для вузов / Т.И. Трофимова. 9-е изд. перераб. и доп. Изд-во: Academia, 2007, 560 c.
2. Савельев И.В. Курс физики: учебник: В 3 т. Т.1: Механика. Молекулярная физика / И.В. Савельев. М.:Наука, Гл. ред. физ.-мат. лит.,1989.-352 с.
3. Детлаф А.А. Курс физики: учеб. пособие для втузов / А.А. Детлаф, Б.М. Яворский. М.: Высш.шк.,1989. – 608 с.
4. Сивухин Д.В. Общий курс физики: учебник: в 5т. Т.1: Механика / Д.В. Сивухин. 3-е изд., испр. и доп. М.: Наука, 1989, -575 с.
5. Москаленко А.Г. Физические основы механики: учеб. пособие / А.Г. Москаленко, Е.П. Татьянина, А.А. Щетинин. Воронеж: ГОУВПО “Воронежcкий государственный технический университет”, 2010. 190 с.
6. Механика: методические указания к выполнению лабораторных работ по дисциплине «Физика» для студентов всех специальностей очной формы обучения (№ 243-2010) /ГОУВПО «Воронежский государственный технический университет»; сост. А.Г. Москаленко, И.А. Сафонов, Н.В. Матовых. Воронеж, 2010. 45 с.
7. Методические указанияк выполнению лабораторного практикума по разделу “Молекулярная физика и термо- динамика”для студентов всех специальностей и всех форм обучения (№287-2005) / Воронеж. гос. техн. ун-т; Сост. А.Г. Москаленко, М.Н. Гаршина, Н.В. Матовых, О.В. Мячина, И.А. Сафонов, Б.Г. Суходолов, Е.В. Шведов. Воронеж, 2005. 43 с.
8. Методические указанияк выполнению лабораторного практикума по разделу “Механические колебания и волны”для студентов всех специальностей дневной формы обучения (№298-2005) / Воронеж. гос. техн. ун-т; сост. В.С. Железный, А.Г. Москаленко, И.А. Сафонов, В.А. Евсюков, Н.В. Матовых. Воронеж, 2005, 44 с.
СОДЕРЖАНИЕ
Лабораторная работа №1.0. 1
Расчет погрешностей измерений при определении. 1 объема цилиндра 1
Лабораторная работа №1.1. 5
Определение ускорения свободного падения на машине Атвуда 5
Лабораторная работа №1.2. 12
Определение упругого модуля сдвига стальной проволоки методом крутильных колебаний 12
Лабораторные работы... 15
№1.3. Определение момента инерции методом трифилярного подвеса 15
№1.4. Определение момента инерции металлических колец при помощи маятника Максвелла 15
№1.5а. Исследование основного уравнения динамики вращательного движения и определение момента инерции крестообразного маятника. 15
№1.5б. Определение момента инерции маховика и момента сил трения 15
Лабораторная работа № 1.6. 24
Определение скорости полета пули с помощью баллистического маятника 24
Лабораторная работа № 1.10. 30
Исследование движения тел в жидкости. 30
Лабораторные работы... 34
№ 1.11. Исследование законов колебательного движения физического маятника и определение ускорения свободного падения. 34
№ 1.12. Определение ускорения свободного падения с помощью математического и оборотного маятников 34
№ 1.13. Определение приведенной длины физического маятника и ускорения свободного падения 34
№ 1.14. Изучение резонансных явлений при колебаниях плоской пружины 34
Лабораторные работы... 39
№ 1.15а. Определение скорости звука в воздухе методом стоячей волны 39
№ 1.15б. Определение скорости звука в воздухе методом сдвига фаз 39
Лабораторные работы... 42
№ 1.16 Определение коэффициента внутреннего трения воздуха при различных температурах 42
№ 1.20 Изучение реального газа (Эффект Джоуля-Томсона) 42
Лабораторные работы... 50
№ 1.17. Определение удельной теплоемкости воздуха при постоянном давлении 50
№ 1.18. Определение отношения теплоемкости воздуха при постоянном давлении и постоянном объеме 50
№ 1.19. Определение удельной теплоты кристаллизации и изменения энтропии при охлаждении олова 50
Библиографический список.. 59
Контрольные задания
для зачета по лабораторным работам
по дисциплине «Физика»
«Механика. Молекулярная физика и термодинамика»
для студентов всех специальностей очной формы обучения
Составители:
Москаленко Александр Георгиевич
Гаршина Мария Николаевна
Татьянина Елена Павловна
Бурова Светлана Васильевна
В авторской редакции
Подписано в печать 25.11.2010.
Формат 60  84/16. Бумага для множительных аппаратов.
84/16. Бумага для множительных аппаратов.
Усл. печ. л. 3,9. Уч.-изд. л.3,7. Тираж 50 экз. «С» 303
Заказ №481
ГОУВПО «Воронежский государственный
технический университет»
394026 Воронеж, Московский просп., 14






