Определение упругого модуля сдвига стальной проволоки методом крутильных колебаний

Теоретический минимум

• Упругие напряжения. Нормальное и тангенциальное напряжение. Закон Гука.
• Деформации растяжения и сжатия. Модуль упругости.
• Деформации сдвига. Модуль сдвига. Связь модуля сдвига с модулем Юнга. Коэффициент Пуассона.
• Деформация кручения. Связь модуля кручения с модулем сдвига.
• Энергия упруго деформированных тел.

Контрольные задания

Вариант 1

1. Какие деформации называются упругими? пластическими?

2. Закон Гука для деформации растяжения имеет вид:

1) σ = Е ε. 2) ε = Δ / 3) τ = G γ 4) M = fφ

3. Жесткость трех одинаковых последовательно соединенных пружин равна k. Чему равна жесткость одной пружины?

4. Во сколько раз относительное удлинение проволоки диаметром d ₁ больше, чем проволоки диаметром d ₂ = 2 d ₁, если к концам проволоки приложены одинаковые силы?

5. Вагон массой т = 12 т двигался со скоростью υ = 1 м/с. Налетев на пружинный буфер, он остановился, сжав пружину на x = 10 см. Найти жесткость пружины.

Вариант 2

1. Что называется абсолютным удлинением тела? относительным удлинением?

2. Закон Гука для деформации кручения имеет вид:

1) σ = Е ε. 2) ε = Δ / 3) τ = G γ 4) M = fφ

3. Жесткость куска проволоки равна k. Чему равна жесткость двух половинок этого куска, соединенных параллельно?

4. На рисунке приведена зависимость упругого напряжения σ от относительной деформации ε для двух образцов. Сравните модули упругости образцов.

 

5. Две пружины с жесткостью k ₁ и k ₂ (k ₁ = 2 k ₂) растянуты до одинаковой силы натяжения. Считая деформацию упругой, сравнить работы растяжения пружины.

 

Вариант 3

1. Что называется напряжением? Каково физическое содержание нормального и тангенциального напряжения?

2. Закон Гука для деформации сдвига имеет вид:

1) σ = Е ε 2) ε = Δ / 3) τ = G γ 4) M = fφ

3. Кусок проволоки длиной и жесткостью k разделили на 3 равные части. Чему равна жесткость каждой части?

4. Какие силы надо приложить к концам стальной проволоки с модулем упругости Е = 200 ГПа длиной 4 м и сечением 0,5 мм² для удлинения ее на 2 мм?

5. Пружину растянули на Δ , затем еще на Δ . Найти отношение произведенных работ, считая деформацию упругой.

 

Вариант 4

1. Каков физический смысл модуля Юнга?

2. К проволоке диаметром 2 мм подвешен груз массой 1кг. Определить напряжение, возникающее в проволоке.

3. Два куска проволоки с одинаковыми коэффициентами упругости k соединяют один раз последовательно, другой раз параллельно. Во сколько раз изменится эквивалентная жесткость кусков?

4. Жесткость стального провода равна 10⁴ Н/м. Если к концу троса, сплетенного из 10 таких проводов, подвесить груз массой 200 кг, то каким будет удлинение?

5. Две последовательно соединенные пружины с жесткостями k ₁ и k ₂ (k ₁ = 2 k ₂) растянуты силой F. Найти отношение потенциальных энергий пружины.

 

Вариант 5

1. Каков физический смысл модуля сдвига?

2. Какой максимальной массы груз может выдержать проволока диаметром d, имеющая предел упругости σ_упр?

3. К проволочному образцу подвешен груз массой т. При этом проволока удлиняется на Δ . Каким будет удлинение образца при добавлении еще трех грузов массой т каждый?

4. К проволоке подвесили груз, затем ее согнули пополам и подвесили тот же груз. Как изменятся а) абсолютные удлинения? б) относительные удлинения?

5. Две пружины с жесткостями k ₁ и k ₂ (k ₁ = 2 k ₂) растянули на одинаковую длину. Сравнить работы растяжения пружин, считая деформацию упругой.

 

Вариант 6

1. Каков физический смысл коэффициента Пуассона?

2. Проволока с известным пределом прочности подвеше-на в вертикальном положении за верхний конец. Какую наибольшую длину может иметь проволока, не обрываясь под действием силы тяжести?

3. Жесткость куска проволоки равна k. Чему равна жесткость половины от этого куска?

4. Нижнее основание железного стержня (G = 76 ГПа) диаметром d = 20 см и высотой h = 20 см закреплено неподвижно. На верхнее основание действует сила F = 20 кН. Найти тангенциальное напряжение, возникающее в материале.

5. Стальной стержень (Е = 200 ГПа) растянут так, что напряжение в материале составляет σ = 300 МПа. Найти объемную плотность потенциальной энергии растянутого стержня.

 

Лабораторные работы

№1.3. Определение момента инерции методом трифилярного подвеса

№1.4. Определение момента инерции металлических колец при помощи маятника Максвелла

№1.5а. Исследование основного уравнения динамики вращательного движения и определение момента инерции крестообразного маятника

№1.5б. Определение момента инерции маховика и момента сил трения

Теоретический минимум

• Момент инерции материальной точки и абсолютно твёрдого тела. Расчёт момента инерции тел простейшей формы. Теорема Штейнера.
• Момент силы, момент импульса тела относительно точки и оси. Уравнение моментов.
• Основное уравнение динамики вращательного движения твёрдого тела.
• Момент импульса материальной точки относительно точки и относительно оси. Момент импульса твердого тела. Закон сохранения момента импульса.
• Кинетическая энергия и работа при вращательном движении. Плоское движение твёрдого тела.

Контрольные задания

Вариант 1

1. Четыре маленьких шарика одинаковой массы, жестко закрепленые невесомыми стержнями, образуют квадрат. Чему равно отношение моментов инерции системы , где 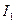- момент инерции относительно оси совпадающей со стороной квадрата, - момент инерции относительно оси совпадающей с его диагональю?

 

2. Определите момент инерции системы относительно оси ОО’ (масса стержня 3m )

 

 

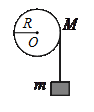
3. Однородный диск массой М приводится во вращение разматывающейся нитью с грузом массой m. Чему равно ускорение груза?

 

 

4. Тонкостенная трубка и кольцо, имеющие одинаковые массы и радиусы, вращаются с одинаковой угловой скоростью. Чему равно отношение величины момента импульса трубки к величине момента импульса кольца.

5. Человек стоит на краю вращающейся по инерции вокруг вертикальной оси карусели. Как изменится частота вращения, если он перейдет в центр карусели?

6. Чему равна полная кинетическая энергия шара массы m, катящегося по горизонтальной поверхности со скоростью ?

 

Вариант 2

1. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на одинаковые расстояния и расставили симметрично относительно оси OO’. Сравните моменты инерции I ₁, I ₂ и I ₃ относительно оси OO’.

2. Определить момент инерции тонкого стержня массой m относительно оси ОО’.

 

3. На рисунке к диску, который может свободно вращаться вокруг оси, проходящей через току О, прикладываются одинаковые по величине силы. В каком положении момент сил будет максимальным?

 

 

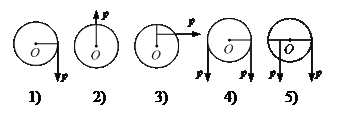
4. Тонкий обруч радиусом R=1м, способный вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 90⁰ и отпустили. Чему равно угловое ускорение обруча в начальный момент времени?

5. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Как изменится частота вращения, если он повернет шест из вертикального положения в горизонтальное?

6. Определите линейную скорость центра шара, скатившегося без скольжения с наклонной плоскости высотой h = 0,1 м.

 

Вариант 3

 

1. Три маленьких шарика расположены в вершинах равностороннего треугольника. Момент инерции этой системы относительно оси О₁, перпендикулярной плоскости треугольника и проходящей через его центр – I₁. Момент инерции этой же системы относительно оси О₂, перпендикулярной плоскости треугольника и проходящей через один из шариков - I₂. Сравните моменты инерции I₁. и I₂.

2. Определите момент инерции проволочного квадрата со стороной d и ее массой m, относительно оси ОО¢.

 

 

 

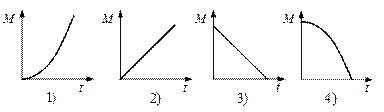
3. Величина момента импульса тела относительно неподвижной оси изменяется по закону , при этом зависимость величины момента сил, действующих на тело, описывается графиком…

 

4. При выстреле орудия снаряд вылетел из ствола, расположенного под углом к горизонту, вращаясь вокруг своей продольной оси с угловой скоростью . Момент инерции снаряда относительно этой оси I=15 кг·м², время движения снаряда в стволе 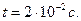Определите момент сил, который действует на ствол орудия во время выстрела.

5. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Как изменится частота вращения карусели в конечном состоянии, если он переместит шест влево от себя?

6. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы вкатываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то какое тело поднимется выше?

 

Вариант 4

1. Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4г. Если поменять местами шарики 2 и 3, то как изменится момент инерции системы относительно оси O, перпендикулярной прямой и проходящей ее середину?

2. Прямолинейная однородная проволока длиной и массой m согнута так, что точка перегиба делит проволоку на две части, длины которых относятся как 1:2. Чему равен момент инерции проволоки относительно оси вращения, проходящей через точку перегиба и перпендикулярной плоскости проволоки?

3. Алюминиевый и стальной цилиндры имеют одинаковую высоту и равные массы. На цилиндры действуют одинаковые по величине силы, направленные по касательной к их боковой поверхности. Сравните моменты сил, действующих на цилиндры.

4. Диск радиуса R и массы m может вращаться вокруг неподвижной оси. На диск намотана нить, к концу которой приложена постоянная сила F. Определите угловое ускорение диска.

 

5. Экспериментатор, стоящий на неподвижной скамье Жуковского получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью 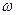. Если экспериментатор повернет ось колеса на угол 180⁰, то он вместе с платформой придет во вращение с угловой скоростью . Чему равно отношение момента инерции экспериментатора со скамьей к моменту инерции колеса?

…

6. Какую долю составляет кинетическая энергия вращательного движения катящегося по горизонтальной поверхности шара от полной кинетической энергии?

 

Вариант 5

1. Как изменится момент инерции тонкого кольца, если ось вращения перенести из центра масс на край?

 

 

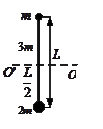2. Чему равен момент инерции системы относительно оси ОО’ (масса стержня 3m)

3. Две материальные точки одинаковой массы движутся с одинаковой угловой скоростью по окружностям радиусами и R₂. Чему равно отношение моментов импульса точек ?

4. Маховик в виде сплошного диска, момент инерции которого I, вращаясь при торможении равнозамедленно, за время t уменьшил частоту вращения n в 2 раза. Найдите выражение для момента силы торможения.

5. Два невесомых стержня длины b соединены под углом a₁ = 180° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На одном конце каждого стержня прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до a₂ = 120°. С какой угловой скоростью стала вращаться система?

6. Для того чтобы раскрутить стержень массы m₁ и длины (см.рисунок) вокруг вертикальной оси, проходящей перпендикулярно через его середину, до угловой скорости 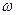, необходимо совершить работу А₁. Какую необходимо совершить работу, для того чтобы раскрутить до той же угловой скорости стержень массы m₂₌m₁/2 и длины ?

 

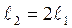Вариант 6

 

1. Тонкостенный и сплошной цилиндры имеют одинаковые массы и радиусы. Сравните моменты инерции этих тел

2.

Если ось ОО¢ перенести из положения 1 в положение 2, то как изменится момент инерции двух материальных точек массами m, соединенных невесомым стержнем длиной L?

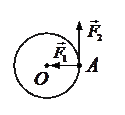3. Чему равна сумма моментов двух сил F₁ = 2H и F₂ = 3Н, приложенных в точке А к диску радиусом R=1 м, вращающемуся относительно оси, прохо-дящей через точку О перпендикулярно плоскости чертежа.?

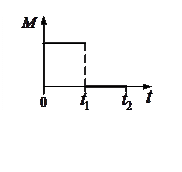4. Диск вращается равномерно с некоторой угловой скоростью 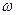. Начиная с некоторого момента времени t=0 на него действует момент сил, график временной зависимости которого представлен на рисунке. Постройте график, отражающий зависимость угловой скорости от времени.

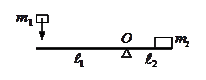5. Тело массой m₁ вертикально падает на свободный конец рычага с плечом ( =2 ) и теряет скорость. Какую скорость приобретает масса m₂ (m₂= 4 m₁) после удара?

 

 

6. Обруч массой m=0,3 кг и радиусом R=0,5м привели во вращение сообщив ему энергию вращательного движения 1200 Дж, и опустили на пол так, что его ось вращения оказалась параллельной плоскости поля. Какую работу совершила сила трения, если обруч начал двигаться без проскальзывания, имея кинетическую энергию поступательного движения 200 Дж?

Вариант 7

1. Определите момент инерции прямоугольной пластинки массы m относительно оси ОО¢.

 

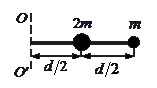
2. Чему равен момент инерции системы относительно оси ОО’ (масса стержня 3m)

 

3. Сплошной цилиндр массы m и радиуса R вращается с угловой скоростью ω вокруг оси Z, совпадающей с одной из образующих цилиндрической поверхности. Найдите выражение для момента импульса цилиндра.

 

4. Диск радиуса R и массы m может вращаться вокруг неподвижной оси. На диск намотана нить, к концу которой приложена постоянная сила F. Чему равна кинетическая энергия диска после того, как он совершит один оборот?

6. Шар и полая сфера имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то какое тело поднимется выше?

5. Момент импульса тела относительно неподвижной оси изменяется по закону L = аt ². Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.

Лабораторная работа № 1.6