389-2010
КОНТРОЛЬНЫЕ ЗАДАНИЯ
для зачета по лабораторным работам по дисциплине «Физика»
«Механика. Молекулярная физика и термодинамика»
для студентов всех специальностей очной формы обучения

Воронеж 2010
Составители: канд. физ.-мат.наук А.Г.Москаленко, канд. техн. наук М.Н. Гаршина, канд. физ.-мат. наук Е.П. Татьянина, канд. физ.-мат. наук С.В. Бурова
УДК 531 (07)
Контрольные задания для зачета по лабораторным работам по дисциплине «Физика» «Механика. Молекулярная физика и термодинамика», для студентов всех специальностей очной формы обучения / ГОУВПО «Воронежский государственный технический университет»; сост. А.Г. Москаленко, М.Н. Гаршина, Е.П.Татьянина, С.В. Бурова. Воронеж, 2010. 61 с.
Методические указания содержат теоретический минимум и варианты контрольных заданий по дисциплине «Физика» для сдачи зачета по лабораторным работам «Механика. Молекулярная физика и термодинамика».
Предназначены для студентов первого курса очной формы обучения всех специальностей.
Библиогр.: 8 назв.
Рецензент д-р. физ.-мат. наук, проф. Е.В. Шведов
Ответственный за выпуск зав. кафедрой профессор В.С.Железный
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
 ГОУВПО «Воронежский
ГОУВПО «Воронежский
государственный технический университет», 2010
Лабораторная работа №1.0
Расчет погрешностей измерений при определении
Объема цилиндра
Теоретический минимум
- Погрешности измерений и их типы.
- Систематическая (приборная) и случайная погреш-ности. Доверительный интервал и доверительная вероятность.
- Методика расчета погрешностей прямых и косвенных измерений.
- Графическое представление результатов измерений.
Контрольные задания
Вариант 1.
1. Табличное значение плотности свинца 11,3·103 кг/м3. Какова абсолютная погрешность представленной величины?
2. Какова приборная погрешность цифрового секундоме-ра, если его показания t =15,28 с?
3. Получить формулу для вычисления абсолютной си-стематической погрешности при определении ускорения свободного падения с помощью математического маятника. Расчетная формула имеет вид:
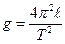 .
.
4. По представленной таблице результатов измерений оценить случайную погрешность и записать в окончательном виде полученный результат. Доверительную вероятность принять равной α=0,9.
| № измерения | x, мм | 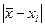 , мм , мм
|  , мм2 , мм2
|
| 30,15 | |||
| 30,10 | |||
| 30,20 | |||
| Ср.знач. |  = =
| 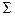 = =
|
5. Округлить среднее арифметическое значение искомой величины  с учетом полученной абсолютной погрешности
с учетом полученной абсолютной погрешности  .
.
Вариант 2
1. Табличное значение плотности стали 7,7·103 кг/м3. Какова абсолютная погрешность представленной величины?
2. Чему равна приборная погрешность штангенциркуля с ценой деления 0,05 мм?
3. Получить формулу для вычисления абсолютной систематической погрешности при определении ускорения равноускоренного движения. Расчетная формула имеет вид:

4. По представленной таблице результатов измерений оценить случайную погрешность и записать в окончательном виде полученный результат. Доверительную вероятность принять равной α=0,9.
| № измерения |  , с , с
|  , с , с
|  , с2 , с2
|
| 12,015 | |||
| 12,021 | |||
| 12,017 | |||
| 12,020 | |||
| 12,018 | |||
| Ср.знач. |  = =
| 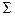 = =
|
5. Округлить среднее арифметическое значение искомой величины  с учетом полученной абсолютной погрешности
с учетом полученной абсолютной погрешности  .
.
Вариант 3
1. Табличное значение модуля Юнга стали 2,16∙107 Па. Какова абсолютная погрешность представленной величины?
2. Чему равна приборная погрешность штангенциркуля с ценой деления 0,1мм?
3. Получить формулу для вычисления абсолютной систематической погрешности при определении плотности шара. Расчетная формула имеет вид:

4. По представленной таблице результатов измерений оценить случайную погрешность и записать в окончательном виде полученный результат. Доверительную вероятность принять равной α= 0,95.
| № измерения | x, мм | 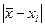 , мм , мм
|  , мм2 , мм2
|
| 30,15 | |||
| 30,10 | |||
| 30,20 | |||
| Ср.знач. |  = =
| 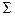 = =
|
5. Округлить среднее арифметическое значение искомой величины  с учетом полученной абсолютной погрешности
с учетом полученной абсолютной погрешности  .
.
Вариант 4
1. Табличное значение модуля Юнга меди 1,18∙107 Па. Какова абсолютная погрешность представленной величины?
2. Какова приборная погрешность цифрового вольтметра,
если его показания U=10,575мВ?
3. Получить формулу для вычисления абсолютной систематической погрешности при определении момента инерции диска. Расчетная формула имеет вид:


4. По представленной таблице результатов измерений оценить случайную погрешность и записать в окончательном виде полученный результат. Доверительную вероятность принять равной α=0,95.
| № измерения |  , с , с
|  , с , с
|  , с2 , с2
|
| 2,11 | |||
| 2,13 | |||
| 2,10 | |||
| Ср.знач. |  = =
| 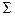 = =
|
5. Округлить среднее арифметическое значение искомой величины  с учетом полученной абсолютной погрешности
с учетом полученной абсолютной погрешности  .
.
Вариант 5
1. Табличное значение температуры плавления алюминия
6590С. Какова абсолютная погрешность представленной величины?
2. Чему равна приборная погрешность микрометра с ценой деления 0,01мм?
3. Получить формулу для вычисления абсолютной систематической погрешности при определении удельного сопротивления проволоки. Расчетная формула имеет вид:

4. По представленной таблице результатов измерений оценить случайную погрешность и записать в окончательном виде полученный результат. Доверительную вероятность принять равной 0,95.
| № измерения | h, мм |  , мм , мм
|  , мм2 , мм2
|
| 10,30 | |||
| 10,35 | |||
| 10,40 | |||
| 10,30 | |||
| Ср.знач. |  = =
| 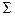 = =
|
5. Округлить среднее арифметическое значение искомой величины  с учетом полученной абсолютной погрешности
с учетом полученной абсолютной погрешности  .
.
Лабораторная работа №1.1
Определение ускорения свободного падения на машине Атвуда
Теоретический минимум
Основные понятия кинематики материальной точки: система отсчета, траектория, путь, перемещение.
Кинематические характеристики движения: скорость, ускорение. Нормальное, тангенциальное и полное ускорение. Кинематическое уравнение движения.
Угловая скорость и ускорение. Связь между линейными и угловыми характеристиками движения.
Закон всемирного тяготения. Сила тяжести и вес тела. Невесомость. Зависимость ускорения свободного падения от широты местности.
Контрольные задания
Вариант 1
1. Указать характер движения в случае an= const, at= f(t)
1) прямолинейное равноускоренное;
2) равномерное вращение по окружности;
3) неравномерное движение по окружности;
4) неравномерное криволинейное движение.
2. Какой смысл имеет выражение  ?
?
3. Зависимость радиус-вектора частицы от времени дается уравнением
 .
.
Чему равна проекция скорости на ось Оx?
4. Материальная точка, двигаясь равноускоренно из состояния покоя, проходит путь S1 за время t1. Путь S2 от начала движения оно пройдет за время t2, равное
1)  2)
2) 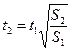 3)
3)  4)
4) 
5. Камень бросили со скоростью  = 10 м/с под углом α = 60° к горизонту. Каков радиус кривизны в высшей точке траектории?
= 10 м/с под углом α = 60° к горизонту. Каков радиус кривизны в высшей точке траектории?
6. Зависимость угла поворота колеса радиусом R = 0,1 м от времени дается уравнением
φ = 3 + 2t +t3 (рад).
Каково нормальное ускорение точек, лежащих на ободе колеса, через 1 с после начала движения?
Вариант 2
1. Перемещение - это
1) линия, по которой движется материальная точка
2) длина линии, по которой движется материальная точка
3) длина траектории материальной точки
4) направленный отрезок прямой линии, соединяющий начальное и конечное положение материальной точки.
2. Смысл выражения  .
.
3. Частица движется со скоростью  , где А = 1 м/с. Чему равен модуль скорости в момент времени
, где А = 1 м/с. Чему равен модуль скорости в момент времени
t = 1 с?
 4. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. Как изменяется при этом величина нормального ускорения?
4. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. Как изменяется при этом величина нормального ускорения?
5. Мяч брошен вертикально вверх из точки, находящейся на высоте h. Чему равен модуль его начальной скорости, если известно, что за время движения мяч пролетел путь 3h?
6. Движение тела с неподвижной осью задано уравнением φ = 2π(6t – 3t2). Начало движения при t = 0. Сколько тело сделает оборотов до момента изменения направления вращения?
Вариант 3
1. При неравномерном движении по окружности справедливы выражения:
1) an = f(t), at = const 3) an = f(t), at = f(t)
2) an = const, at = f(t) 4) an = const, at = const
2. Какой смысл имеет выражение  ?
?
3. Частица движется со скоростью  , А = 1 м/с. Чему равен модуль ускорения в момент времени t=1с?
, А = 1 м/с. Чему равен модуль ускорения в момент времени t=1с?
 4.Какова средняя скорость тела, свободно падающего с высоты H на Землю?
4.Какова средняя скорость тела, свободно падающего с высоты H на Землю?
5. Камень бросили под углом  к горизонту со скоростью
к горизонту со скоростью  . Как изменяется модуль тангенциального ускорения aτ на участке АВ?
. Как изменяется модуль тангенциального ускорения aτ на участке АВ?
6. Твердое тело вращается вокруг неподвижной оси по закону φ = 6t – 2t3. Чему равен модуль углового ускорения в момент остановки тела?
Вариант 4
1. Тангенциальная составляющая ускорения характеризует
1) изменение направления скорости;
2) быстроту изменения скорости по модулю;
3) быстроту изменения скорости и по модулю, и по направлению;
4) увеличение модуля скорости.
 2. Материальная точка M движется по окружности. График зависимости
2. Материальная точка M движется по окружности. График зависимости 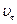 от времени представлен на рисунке. Укажите направление полного ускорения точки М.
от времени представлен на рисунке. Укажите направление полного ускорения точки М.
3. Зависимость радиус-вектора частицы от времени дается уравнением
 .
.
Чему равна проекция ускорения на ось Oy?
4. Тело движется равномерно из состояния покоя с ускорением а. Чему равен путь, пройденный за n–ю секунду?
5. Тело брошено с начальной скоростью  под углом
под углом  к горизонту. Нарисовать траекторию тела и показать векторы нормального и тангенциального ускорений в точках, соответствующих началу движения и наивысшей точке подъема.
к горизонту. Нарисовать траекторию тела и показать векторы нормального и тангенциального ускорений в точках, соответствующих началу движения и наивысшей точке подъема.
6. Зависимость угла поворота колеса радиусом R = 0,1 м от времени дается уравнением
φ = 3 + 2t +t3 (рад).
Чему равно через 1 с после начала движения нормальное ускорение точек, лежащих на ободе колеса?
Вариант 5
1. При неравномерном криволинейном движении справедливы выражения:
1) an = const, at = 0 2) an = const, at = f(t)
3) an = f(t), at = f(t) 4) an = 0, at = const
2. Какой смысл имеет выражение  ?
?
3. Частица движется вдоль оси Ox по закону
х = -19 + 20t - t2.
 Чему равна в момент времени t = 5 с проекция ускорения частицы на ось Oх?
Чему равна в момент времени t = 5 с проекция ускорения частицы на ось Oх?
 4. График зависимости координаты тела от времени прямолинейного движения представлен на рисунке. Движению этого тела соответствует график зависимости проекции скорости от времени
4. График зависимости координаты тела от времени прямолинейного движения представлен на рисунке. Движению этого тела соответствует график зависимости проекции скорости от времени
 5. Два тела брошены под углом к горизонту так, что проекции их начальных скоростей на вертикальную ось отличаются в два раза. Чему равно отношение их времени полета t1/t2, до падения при полете над горизонтальной плоскостью?
5. Два тела брошены под углом к горизонту так, что проекции их начальных скоростей на вертикальную ось отличаются в два раза. Чему равно отношение их времени полета t1/t2, до падения при полете над горизонтальной плоскостью?
6. Вал вращающийся с частотой n = 180 об/мин, начал двигаться равнозамедленно с угловым ускорением e = 3 рад/с2. Чему равно время до остановки?
Вариант 6
1. Что означает выражение 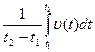 ?
?
2. Нормальное ускорение характеризует быстроту изменения…
1) направления скорости;
2) направления и величины скорости;
3) величины скорости;
4) направления перемещения.
3. Зависимость радиус-вектора частицы от времени дается уравнением
 .
.
Чему равен модуль ускорения?
4. Зависимость координаты тела от времени имеет вид:
x=10+2t2+5t (м).
Чему равна средняя скорость тела за первые 5 секунд движения?
5. Тело брошено под углом 60° к горизонту. Чему равно тангенциальное ускорение камня в начальный момент движения?
6. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением j(t)=2p(t2-6t+12)(рад). В какой момент времени частица остановится?
Вариант 7
1. Тангенциальная составляющая ускорения направлена
1) произвольно;
2) перпендикулярно касательной к траектории к центру ее кривизны;
3) вдоль касательной к траектории в данной ее точке;
4) перпендикулярно касательной к траектории от центра ее кривизны.
2. Какой смысл имеет выражение  ?
?
3. Движение частицы определяется уравнениями x=4t, y=2t2. Каков угол между вектором скорости  и вектором ускорения
и вектором ускорения  в момент времени t = 1 с?
в момент времени t = 1 с?
4.Камень бросили со скоростью υ = 10 м/с под углом α = 60° к горизонту. Каков радиус кривизны траектории в начальный момент времени?
5. С крыши с интервалом времени 1с падают одна за другой две капли. Каково расстояние между каплями через 2с после начала падения второй капли?
6. Частица из состояния покоя начала двигаться по дуге окружности радиуса R = 1 м с постоянным угловым ускорением e = 2 с-2 .Чему равно отношение нормального ускорения к тангенциальному через одну секунду?
Вариант 8
1. Какой смысл имеет выражение  ?
?
2. При равномерном вращении по окружности выполняются соотношения:
1) an = const, at = 0 2) an = const, at = f(t)
3) an = f(t), at = f(t) 4) an = 0, at = const
3. Частица ударяется о стенку под углом a к ней и упруго отражается. Чему равен модуль приращения скорости ï∆  ï?
ï?
 4.Тело брошено под углом 30° к горизонту. Чему равно тангенциальное ускорение камня в начальный момент движения?
4.Тело брошено под углом 30° к горизонту. Чему равно тангенциальное ускорение камня в начальный момент движения?
5. Твердое тело начинает вращаться вокруг оси Oz. Зависимость проекции углового ускорения ez на ось Oz меняется от времени t согласно графику. Такому движению соответствует график зависимости проекции угловой скорости wz от времени…
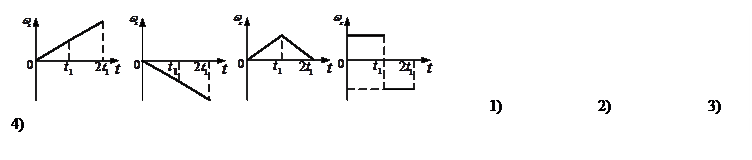
6. Твердое тело вращается вокруг неподвижной оси по закону φ = 6t – 2t3.
Чему равно среднее значение угловой скорости за промежуток времени от t = 0 до остановки?
Лабораторная работа №1.2






