Пример 16. Найти градиент функции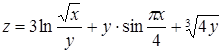 
в точке
М (4; 2) и производную по направлению вектора 
Решение. Найдем частные производные
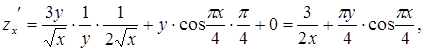
и
Вычислим значения частных производных в точке М:
Таким образом, градиентом функции будет вектор:
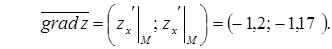
Производную по направлению вектора 
найдем по формуле:
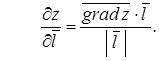
Ответ: 
Дифференциальные уравнения
Пример 17. Решить задачу Коши:
Решение. 1) Найдем общее решение дифференциального уравнения. Данное дифференциальное уравнение первого порядка является линейным. Следовательно, произведем следующую замену переменной:
Тогда
Подберем теперь такую функцию v (x), чтобы v ¢+2 xv =0. То есть v (x) будем искать как решение дифференциального уравнения с разделяющимися переменными:
При С = 0 получим: ln| v | = - x 2. Следовательно, 
.
При таком выборе функции v (x) исходное дифференциальное уравнение примет вид: 
Следовательно, 
Таким образом,
2) Для решения задачи Коши воспользуемся начальным условием y (0)=0.
Тогда 
Ответ: 
.
КОНТРОЛЬНАЯ РАБОТА
Задание №1. Решить систему линейных уравнений:
1) методом Гаусса; 2) методом Крамара; 3) с помощью обратной матрицы.
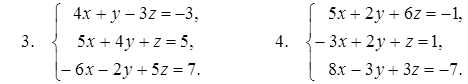
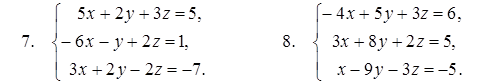
Задание №2. Дана пирамида ABCD. Найти: 1) угол CBD; 2) площадь грани ABC; 3) объем пирамиды.
1. A(2; 4;-3), B(-1; 3; 5), C(6;-2; 1), D(-2;-3; 4).
2. A(4; 2; 3), B(1;-4; 5), C(2;-4;-1), D(-3; 2; 3).
3. A(-1; 3; 3), B(7; 2; 0), C(-2;-1; 4), D(4; 3; -1).
4. A(-2; 5; 6), B(0; 5;-8), C(-3; 2; 4), D(5; -2; 6).
5. A(1; 5; 3), B(7; 0; -1), C(-6; 2; 3), D(-2; 3; 3).
6. A(2; 4;-3), B(-1; 3; 5), C(3; -2; 1), D(2; 3;-7).
7. A(3; 0; 5), B(-4; 3; -1), C(-5; 2; 3), D(1; 1; 4).
8. A(5;-2; 1), B(-2;-3; 0), C(7;-1;-1), D(-1; 0; 5).
9. A(-3; 1; 0), B(4; 1; -5), C(-6; 1; 1), D(3;-1;-1).
10. A(-7; 1;-5), B(3; -6; 1), C(4;-1; 4), D(2; 5; 0).
Задание №3. Дан треугольник ABC. Найти: 1) уравнения сторон;
2) уравнение и длину медианы AM; 3) уравнение и длину высот BD и CK;
4) уравнение биссектрисы угла B; 5) точку пересечения медианы АМ с высотой BD и угол между ними.
| 1. A(2; 3), B(-4; 3), C(-1; -1). | 2. A(-2; 4), B(-2; 1), C(1; 5). |
| 3. A(4; 1), B(3; 1), C(0; -3). | 4. A(3; -2), B(3; 0), C(-1; -3). |
| 5. A(6; 4), B(-3; 4), C(1; 1). | 6. A(-2; 2), B(-2; 6), C(1; 10). |
| 7. A(5; 1), B(3; 1), C(-1; -2). | 8. A(3; 0), B(3; -6), C(0; -2). |
| 9. A(-2; 3), B(4; 3), C(1; -1). | 10. A(6; 1), B(6; -3), C(3; -1). |
Задание №4. Найти предел следующих функций:
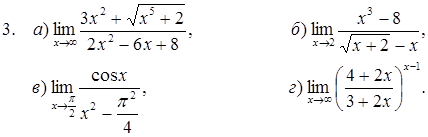
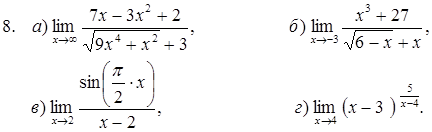
Задание №5. Найти производную y¢ (x) следующих функций:
Задание №6. Вычислить приближенно, с помощью дифференциала:
Задание №7. Найти неопределенный интеграл:
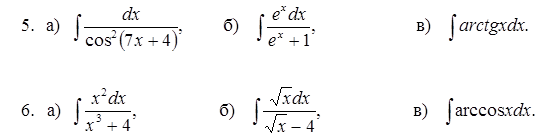
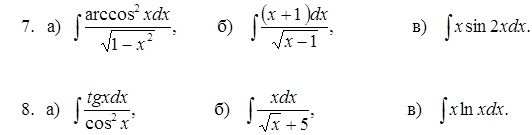
Задание №8. С помощью определенного интеграла вычислить площадь земельного участка, ограниченного линиями:
Задание №9. Найти градиент функции z = z (x; y) в точке М и производную по направлению вектора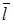 
.
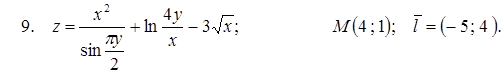
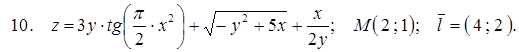
Задание №10. Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию (задача Коши):
ЧАСТЬ III
Программа 3-го семестра
(зачет)
1. Случайные события. Классическое, статистическое и геометрическое определение вероятности.
2. Алгебра событий. Теоремы сложения и умножения вероятностей.
3. Формула полной вероятности
4. Формула Бернулли. Локальная и интегральная теоремы Лапласа.
5. Дискретные случайные величины. Закон распределения случайной величины. Законы биномиальный и Пуассона.
6. Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Закон больших чисел.
7. Непрерывные случайные величины. Функция распределения и плотность распределения.
8. Числовые характеристики непрерывных случайных величин.
9. Равномерное, нормальное и показательное распределения.
10. Выборочный метод. Эмпирическая функция распределения. Полигон и гистограмма.
11. Точечные и интервальные оценки параметров распределения.
12. Корреляция. Линейная и криволинейная корреляция.
13. Коэффициент корреляции. Линии регрессии.
14. Множественная корреляция.
15. Статистическая проверка статистических гипотез.
