printf("\n Reshenie sistemy uravn.:\n");
for (i=0; i<n; i++)
printf("%10.5f", x[i]);
printf("\n");
Return 0;
}
Результат работы программы:
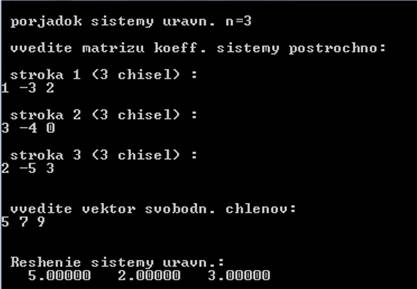
Таким образом,
x1=5.0 x2=2.0 x3=3.0
Решение системы линейных алгебраических уравнений
итерационным методом Гаусса-Зайделя
В головной программе необходимо:
1. описать прототип функции решения системы уравнений:
int Gauss_Zaidel(int n, float a[n][n], float b[n], float eps, int count, float x[n]);
2. ввести значение переменной n – порядок системы уравнений,
3. описать массивы:
float a[n][n]; // матрица коэффициентов системы уравнений
float b[n]; // матрица свободных членов
float x[n]; // вектор решения (вектор неизвестных)
4. ввести массивы a[n][n] и b[n],
5. ввести погрешность вычислений eps и максимальное количество итераций count,
6. обратиться к программе решения системы уравнений:
Gauss_Zaidel(n, a, b, eps, count, x);
7. вывести на экран терминала (в текстовый файл) вектор решения.
Пример: решить систему уравнений
x1 + 0,17x2 - 0,25x3 + 0,54x4 = 0,3;
0,47x1 + x2 + 0.67x3 - 0,32x4 = 0,5;
-0,11x1 + 0,35x2 + x3 - 0,74x4 = 0,7;
0,55x1 + 0,43x2 + 0,36x3 - x4 = 0,9;
В этом случае n=4;
1.0 0,17 0,25 0,54 0,3
a[4][4]= 0,47 1.0 0.67 0,32 b[4] = 0,5
-0,11 0,35 1.0 0,74 0,7
0,55 0,43 0,36 1.0 0,9
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int Gauss_Zaidel(int n, float a[n][n], float b[n], float eps, int count, float x[n]);
int main(int argc, char **argv)
{
int n; // порядок системы уравнений
int count; // заданное количество итераций
int i,j; // рабочие переменных
printf("\n porjadok sistemy uravn. n=");
scanf("%d", &n);
float a[n][n]; // матрица коэффициентов системы уравнений
float b[n]; // вектор свободных членов
float x[n]; // вектор решения системы уравнений
float eps; // заданная точность вычислений
printf("\n vvedite matrizu koeff. sistemy postrochno:\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n");
printf("\n vvedite vektor svobodn. chlenov (%d chisel):\n", n);
for (i=0; i<n; i++)
scanf("%f", &b[i]);
printf("\n");
printf("\n pogreshn. vychisl. eps=");
scanf("%g", &eps);
printf("\n max kolich. iteraciy count=");
scanf("%d", &count);
Gauss_Zaidel(n, a, b, eps, count, x);
printf("\n Reshenie sistemy uravn.:\n");
for (i=0; i<n; i++)
printf("%10.5f", x[i]);
printf("\n");
Return 0;
}
Результат работы программы:

Таким образом,
x1=0.441 x2=-0.363 x3=1.667 x4=0.3935
Решение системы несовместных линейных уравнений
методом наименьших квадратов
В головной программе необходимо:
1. описать прототип функции решения системы уравнений:
int nesovmest(int n, int kk, float a[kk][n], float b[kk], float x[n], float y[kk], float *s0);
2. ввести значение переменной n – порядок системы уравнений,
3. ввести значение переменной k – количество уравнений (k>n),
4. описать массивы:
float a[n][n]; // матрица коэффициентов системы уравнений
float b[n]; // матрица свободных членов
float x[n]; // вектор оценок неизвестных
float y[n]; // вектор невязок
5. ввести массивы a[n][n] и b[n],
6. обратиться к программе решения системы уравнений:
nesovmest(n, k, a, b, x, y, &s0);
7. вывести на экран терминала (в текстовый файл) вектор оценок неизвестных, вектор невязок и среднеквадратическую невязку
Пример: решить систему уравнений
2x1 + 3x2 = 5;
x1 - 2x2 = 7;
2x1 - x2 = 8;
В этом случае n=2, k=3;
2 3 5
a[3][2]= 1 -2 b[3]= 7
2 -1 9
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int nesovmest(int n, int kk, float a[kk][n], float b[kk], float x[n], float y[kk], float *s0);
int main(int argc, char **argv)
{
int n; // количество неизвестных
int k; // количество уравнений (k>n)
float s0; // среднеквадратическая невязка
int i,j; // рабочие переменные
printf("\n Kol-vo neizvestn. n=");
scanf("%d", &n);
printf("\n Kol-vo uravnen. (k>n) k=");
scanf("%d", &k);
float a[k][n]; //матрица коэффициентов системы уравнений
float b[k]; // вектор свободных членов
float x[n]; // вектор оценок неизвестных
float y[k]; // вектор невязок
printf("\n vvedite matrizu koeff. sistemy postrochno:\n");
for (i=0; i<k; i++)
{
printf("\n stroka %d (%d znachenij):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n");
printf("\n vvedite vektor svobodn. chlenov (%d znachenij):\n", k);
for (i=0; i<k; i++)
scanf("%f", &b[i]);
printf("\n");
nesovmest(n, k, a, b, x, y, &s0);
printf("\n Ocenki neizvestnyh:\n");
for (i=0; i<n; i++)
printf("%10.5f", x[i]);
printf("\n");
printf("\n Vector nevjazok:\n");
for (i=0; i<k; i++)
printf("%10.5f", y[i]);
printf("\n");
printf("\nSrednekv. nevjazka: %e\n", s0);
Return 0;
}
Результат работы программы:

Таким образом,
x1=3.902 x2=-1.057
Решение системы нелинейных и трансцендентных уравнений
методом Стеффенсена
В головной программе необходимо:
1. описать прототип функции решения системы уравнений:
int Steffensen(int n, float eps, int count, float x[n], float y[n]);
2. ввести значение переменной n – количество неизвестных,
3. ввести значение переменной eps – погрешность вычислений,
4. ввести значение переменной count – заданное количество итераций,
5. описать массивы:
float x[n]; // вектор решения системы уравнений
float y[n]; // вектор невязок
6. описать систему уравнений в функции:
void pr_chasti(int n, float x[n], float b[n])
в виде b[i]=b(x[j]); i,j=0…n-1,
7. ввести массив x[n] – вектор начальных приближений неизвестных,
8. обратиться к программе решения системы уравнений:






