2. описать подынтегральное выражение в функции float function(float x):
Float function(float x)
{
return sqrt(1.0-(x-1.0)*(x-1.0)); // формула полуокружности
}
3. ввести значение переменных x_nach и x_kon – нижний и верхний пределы интегрирования,
4. ввести значение переменной n – количество участков интегрирования (формула интегрирования), n<10:
n=1 - формула трапеций,
n=2 - формула Симпсона,
n=3 - формула трех восьмых,
n=4 - формула Бодэ,
n=5 - формула Дьяконова,
5. обратиться к программе вычислений:
integral=integral_Newton_Kotes(n, x_nach, x_kon);
6. вывести на экран терминала (в текстовый файл) значение интеграла.
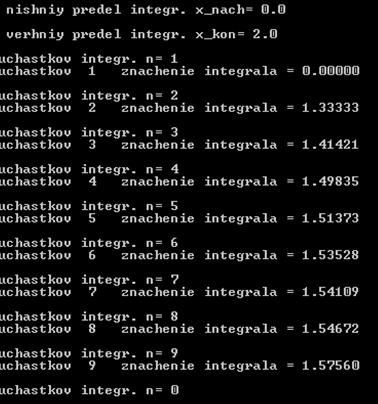
Пример: найти значение интеграла от полуокружности единичного радиуса
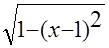в пределах от 0,0 до 2,0 (точное значение интеграла равно
π/ 2=1,570796 …) для n=1…9.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
Float integral_Newton_Kotes(int n, float x_nach, float x_kon);
int main(int argc, char **argv)
{
int n; // количество участков интегрирования
//(метод интегрирования):
// 1 - метод трапеций,
// 2 - метод Симпсона,
// 3 - метод трех восьмых,
int i; // рабочая переменая
float x_nach, x_kon; // нижний и верхний пределы
// интегрирования
float integral; // значение интеграла
printf("\n nishniy predel integr. x_nach= ");
scanf("%f", &x_nach);
printf("\n verhniy predel integr. x_kon= ");
scanf("%f", &x_kon);
Do
{
printf("\nuchastkov integr. n= ");
scanf("%d", &n);
if (n==0)
Break;
integral=integral_Newton_Kotes(n, x_nach, x_kon);
printf("uchastkov %d znachenie integrala = %1.5f\n", n, integral);
}
While (1);
Return 0;
}
Описание подынтегральной функции:
Float function(float x)
{
return sqrt(1.0-(x-1.0)*(x-1.0));
}
Результат работы программы:
Топологический анализ ориентированных графов
В головной программе необходимо:
1. описать прототип функции:
void topolog(int n, int v1, int v2, float s[n][n], int puti_i_kontury, int *contur, int *path, int t[puti_i_kontury][n+1], float dlina[puti_i_kontury]);
2. ввести значение переменной n – количество вершин в графе,
3. ввести значение переменных v1, v2 – номера вершин входа и выхода,
4. описать массив s[n][n] – матрица смежности графа:
если вершина k не связана с вершиной m ребром, то s[k][m] = 0, в противном случае этот элемент матрицы равен длине этого ребра,
5. описать массивы:
int t[puti_i_kontury][n+1] – матрица прямых путей “вход-выход” и замкнутых контуров графа: первые path строк – пути, остальные – замкнутые контура,
float dlina[puti_i_kontury] - длины путей и контуров,
6. ввести массив s[n][n] из текстового файла или с кловиатуры,
7. обратиться к программе вычислений:
topolog(n, v1, v2, s, puti_i_kontury, &contur, &path, t, dlina);
8. вывести на экран или в текстовый файл:
path – количество прямых путей “вход-выход”,
contur – количество замкнутых контуров,
t[puti_i_kontury][n+1] -матрицу прямых путей “вход-выход” и замкнутых контуров графа,
dlina[puti_i_kontury] - длину путей и контуров.
Пример: произвести топологический анализ следующего графа:
 |
Найти все прямые пути от входа 1 до выхода 6.
В этом случае n=6, v1=1, v2=6 и матрица смежности имеет вид (длина всех ребер – единица):
0 1 0 1 0 0
0 0 1 0 1 0
s[6][6]= 0 0 0 0 0 1
0 0 1 0 1 0
1 0 0 0 0 1
0 0 0 0 0 0
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void topolog(int n, int v1, int v2, float s[n][n], int puti_i_kontury, int *contur, int *path, int t[puti_i_kontury][n+1], float dlina[puti_i_kontury]);
int main(int argc, char **argv)
{
int n; // количество вершин в графе
int v1; // номер вершины-входа
int v2; // номер вершины-выхода
int puti_i_kontury; // количество путей и контуров
char path_input[30]="E:/User/topolog_inp_6.txt";
// полный путь к текстовому файлу для ввода данных,
char path_output[30]="E:/User/topolog_out_6.txt";
// полный путь к текстовому файлу для вывода данных
int contur; // количество замкнутых контуров в графе
int path; // количество прямых путей "вход-выход"
int i, j, i1, j1; // рабочие переменные
Char c0;
printf("\nKol-vo vershin n= ");
scanf("%d", &n);
float s[n][n]; // матрица смежности графа:
// если вершина k связана с вершиной m
// ребром длиной d,
// то s[k][m]=d, иначе s[k][m]=0.0
printf("\nNomer vhoda v1= ");
scanf("%d", &v1);
printf("\nNomer vyhoda v2= ");
scanf("%d", &v2);
printf("\nMax. kol-vo putej i konturov (predpoloshit.) puti_i_kontury= ");
scanf("%d", &puti_i_kontury);
int t[puti_i_kontury][n+1]; // матрица путей и контуров:
// в ее первых path строках –
// последовательность номеров вершин,
// образующих прямые пути от
// вершины-входа до вершины-выхода,
// в последующих contur строках –
// последовательность номеров вершин,
// образующих замкнутые контуры в графе.
float dlina[puti_i_kontury]; // длина прямых путей
// и контуров
FILE *f_input;
f_input=fopen(path_input, "r"); // файл для ввода данных
if (f_input==0)
{
printf("Error input!");
Return 1;
}
for (i=0; i<n; i++)
for (j=0; j<n; j++)
fscanf(f_input, "%f", &s[i][j]);
Fclose(f_input);
topolog(n, v1, v2, s, puti_i_kontury, &contur, &path, t, dlina);
FILE *f_output;
f_output=fopen(path_output, "w"); // файл для вывода данных
if (f_output==0)
{
printf("Error output!");
Return 1;
}
if (path>0)
{
printf("\n");
printf("V grafe:\n");
printf("\nvsego putey - %3d\n", path);
printf("\nPuti ot %2d do %2d:\n",v1,v2);
printf("Puty vershiny dlina\n");
fprintf(f_output, "\n");
fprintf(f_output, "V grafe:\n");
fprintf(f_output, "\nvsego putey - %3d\n", path);
fprintf(f_output, "\nPuti ot %2d do %2d:\n",v1,v2);
fprintf(f_output, "Puty vershiny dlina\n");
for (i=1; i<=path; i++)
{
printf("%3d ", i);
fprintf(f_output, "%3d ", i);
for (j=1; j<=n; j++)
{
i1=t[i-1][j-1];
j1=t[i-1][j];
if (i1!=0)
{
printf("%4d", i1);
fprintf(f_output, "%4d", i1);
}
}
printf(" %0.2f\n", dlina[i-1]);
fprintf(f_output, " %0.2f\n", dlina[i-1]);
}
}
if (contur>0)
{
printf("\n");
printf("\nvsego konturov - %3d\n", contur);
printf("Kontur vershiny dlina\n");
fprintf(f_output, "\n");
fprintf(f_output, "\nvsego konturov - %3d\n", contur);
fprintf(f_output, "Kontur vershiny dlina\n");
for (i=1; i<=contur; i++)
{
i1=i+path;
printf("%3d ", i);
fprintf(f_output, "%3d ", i);
for (j=1; j<=n+1; j++)
{
j1=t[i1-1][j-1];
if (j1!=0)
{
printf("%4d", j1);
fprintf(f_output, "%4d", j1);
}
}
printf(" %0.2f\n", dlina[i1-1]);
fprintf(f_output, " %0.2f\n", dlina[i1-1]);
}
}
Fclose(f_output);
c0=getch();
Return 0;
}
Результат решения задачи:
