8. вывести на экран терминала (в текстовый файл) матрицы f[n][n] и c[n][m].
Пример: определить дискретный аналог динамической системы:
dx1/dt = x2(t) – 0,5u1(t) + 0,2u2(t);
dx2/dt = x3(t) + u1(t) - u2(t);
dx3/dt = -2x1(t) – 3x2(t) – 3x3(t) - 0,1u1(t) + 5u2(t);
для интервала дискретности h0=0,1 c.
В этом случае n=3, m=2,
0 1 0 -0.5 0.2
a = 0 0 1 b = 1 -1
-2 -3 -3 -0.1 5
Собственные значения исходной системы:
p = -2 -0.5 0.5
0 -0.866 0.866
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void diskret_analog(int n, int m, float h0, float a[n][n], float b[n][m], float p[2][n], float f[n][n], float c[n][m]);
int main(int argc, char **argv)
{
int n; // количество фазовых координат
int m; // количество управлений
float h0; // интервал дискретности
int i, j; // рабочие переменные
Char c0;
printf("\n Kol-vo fazov. koordinat n= ");
scanf("%d", &n);
printf("\n Kol-vo upravlen. m= ");
scanf("%d", &m);
printf("\n Interval diskretn. h0 =");
scanf("%f", &h0);
printf("\n");
float a[n][n]; // матрица динамики исходной системы
float b[n][m]; // матрица управления исходной системы
float p[2][n]; // матрица собственных значений
// исходнойсистемы:
// первая строка - действительные части,
// вторая строка - мнимые части,
// комплексные собств. значения
// вводить парами, первым –
// с отрицательной мнимой частью,
float f[n][n]; // фундаментальная матрица дискретного
// аналога для интервала дискретности h0
float c[n][m]; // матрица управления дискретного
// аналога для интервала дискретности h0
printf("\nVvedite matricu dinamiki postrochno (%d znashenij v stroke):\n", n);
for (i=0; i<n; i++)
{
printf("\n%d stroka:\n", i+1);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n");
printf("\nVvedite matricu upravlenija postrochno (%d znashenij v stroke):\n", m);
for (i=0; i<n; i++)
{
printf("\n%d stroka:\n", i+1);
for (j=0; j<m; j++)
scanf("%f", &b[i][j]);
}
printf("\n");
printf("\nVvedite dejstvit. chasti sobstv. znachenij (%d znashenij):\n", n);
for (i=0; i<n; i++)
scanf("%f", &p[0][i]);
printf("\n");
printf("\nVvedite mnimye chasti sobstv. znachenij (%d znashenij):\n", n);
for (i=0; i<n; i++)
scanf("%f", &p[1][i]);
printf("\n");
Diskret_analog(n, m, h0, a, b, p, f, c);
printf("\nFundament. matrica discretnogo analoga:\n");
for (i=0; i<n; i++)
{
for (j=0; j<n; j++)
printf("%15.6e ", f[i][j]);
printf("\n");
}
printf("\n");
printf("\nMatrica upravl. discretnogo analoga:\n");
for (i=0; i<n; i++)
{
for (j=0; j<m; j++)
printf("%15.6e ", c[i][j]);
printf("\n");
}
printf("\n");
c0=getch();
Return 0;
}
Результат работы программы:

Определение дискретного аналога передаточной функции
методом Тастина
В головной программе необходимо:
1. описать прототип функции:
void tastin(int n, float h0, float w[2][n+1]);
2. ввести значение переменной n – степень полинома знаменателя,
3. ввести значение переменной h0 – интервал дискретности,
4. описать массивы:
w[2][n+1] – матрица коэффициентов исходной передаточной функции по возрастающим степеням:
первая строка – числитель,
вторая строка – знаменатель,
после вычислений – массив коэффициентов дискретной передаточной функции по возрастающим степеням,
5. ввести массив w [2][n+1]
6. обратиться к программе вычислений:
Tastin(n, h0, w)
7. вывести на экран терминала (в текстовый файл) матрицу w[2][n+1].
Пример: определить дискретный аналог передаточной функции:
W(p) = (0,5p + 1) / (6p3 + 11p2 + 6p + 1)
для интервала дискретности h0 = 0,5 c.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void tastin(int n, float h0, float w[2][n+1]);
int main(int argc, char **argv)
{
int n; // степень полинома знаменателя
float h0; // период дискретности
Int i;
Char c;
printf("\n stepen polinoma znamenat. n= ");
scanf("%d", &n);
printf("\nVvedite period diskretn. h0 =");
scanf("%f", &h0);
printf("\n");
float w[2][n+1]; //матрица коэффициентов исходной
// передаточной функции по возраст.
// степеням:
// первая строка - числителя,
// вторая строка - знаменателя,
// после вычислений - массив коэфф.
// дискретной передаточной функции
// по возраст. степеням
printf("\nVvedite koeff. chislitelja (%d znacheniy):\n", n+1);
for (i=0; i<n+1; i++)
scanf("%f", &w[0][i]);
printf("\nVvedite koeff. znamenatelja (%d znacheniy):\n", n+1);
for (i=0; i<n+1; i++)
scanf("%f", &w[1][i]);
printf("\n");
Tastin(n, h0, w);
printf("\nKoefficienty chislit. diskretn. peredat. funkcii:\n");
for (i=0; i<n+1; i++)
printf("%e ", w[0][i]);
printf("\n\n");
printf("\nKoefficienty znamenat. diskretn. peredat. funkcii:\n");
for (i=0; i<n+1; i++)
printf("%e ", w[1][i]);
printf("\n\n");
c=getch();
Return 0;
}
Результат работы программы:
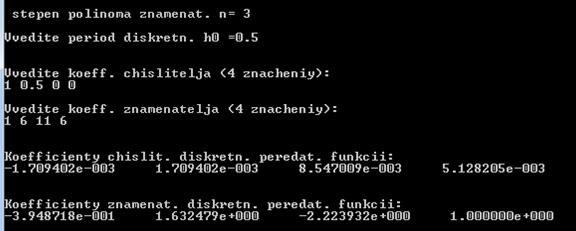
Таким образом, дискретный аналог исходной передаточной функции для интервала дискретности h0 = 0,5 имеет вид:
W(z)=(-1,7094×10-3 z-3 +1,7094×10-3 z-2 +8,547×10-3z-1 +5,1282×10-3z) / (-0,39487 z-3 + 1,6325 z-2 – 2,2239 z-1 + z)
Расчет выходного сигнала динамической системы,
заданной передаточной функцией
В головной программе необходимо:
1. описать прототип функции:






