1. Определенный интеграл является числом, не зависящим от выбора обозначения переменной интегрирования, т. е.
.
2. Если функция f (x) определена в точке a, то
.
3. Если функция f (x) интегрируема на отрезке [ a, b ], то при замене пределов интегрирования меняется знак:
.
4. Если функции f (x) и g(x) интегрируемы на отрезке [ a, b ], 
и 
— постоянные множители, то функция 
тоже интегрируема на этом отрезке, причем
.
5. Если функция f (x) интегрируема на отрезках [ a, c ] и [ c, b ], то она интегрируема и на отрезке [ a, b ], причем
.
Геометрически этот факт иллюстрируется рис. 7.3.
 |
Рис. 7.3. Разбиение площади под кривой на две фигуры
Можно утверждать обратное. Если функция интегрируема на отрезке [ a, b ], то она интегрируема и на любой части этого отрезка.
6. Если функция f (x) непрерывна на отрезке [ a, b ], то она интегрируема на этом отрезке, причем существует точка c 
[ a, b ] такая, что справедливо равенство
.
Это свойство, иллюстрируемое рис. 7.4, часто называют теоремой о среднем значении или просто теоремой о среднем.
 |
Рис. 7.4. Пояснение теоремы о среднем
Формула Ньютона-Лейбница
Пусть функция f (x) непрерывна на отрезке [ a, b ], следовательно, по свойству 6 она интегрируема на этом отрезке. Выберем произвольную точку x 
[ a, b ]. Тогда f (x) также интегрируема на отрезке [ a, x ] по свойству 5.
Рассмотрим функцию
,
которая называется интегралом с переменным верхним пределом. Докажем, что функция F 1(x) является первообразной для функции f (x) на отрезке [ a, b ].
Дадим переменной x приращение 
x так, что x + 
x [ a, b ]. Тогда приращение функции
.
Воспользуемся теоремой о среднем
, с [ x, x + x ].
По определению производной
.
Таким образом, доказано, что функция F 1(x) является первообразной для f (x) на отрезке [ a, b ].
Возьмем какую-либо другую первообразную F (x) для f (x). По теореме о первообразных функциях
F (x) = F 1(x) + C,
т. е. 
на отрезке [ a, b ].
Рассмотрим значения F (x) на концах отрезка [ a, b ].
;
.
Отсюда
.
Перейдя по свойству 1 к переменной интегрирования x и вводя обозначение, называемое символом двойной подстановки, имеем
,
окончательно запишем основную формулу интегрального исчисления — формулу Ньютона-Лейбница.
.
Формула Ньютона-Лейбница позволяет вычислять определенный интеграл, если существует первообразная F (x) подынтегральной функции f (x).
Следует помнить, что эта формула была получена в предположении, что f (x) непрерывна на отрезке [ a, b ]. Поэтому, если на этом отрезке есть точка разрыва подынтегральной функции, то формула Ньютона-Лейбница в общем случае неприменима.
Пример 7.25.
Вычислить определенные интегралы:
1. 
.
2. 
.
3. 
.
4. 
.
7.5. Вычисление площадей плоских фигур
Пусть функция у = f (x) неотрицательна и непрерывна на отрезке [ а, b ]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой у = f (x)на [ а, b ]численно равна определенному интегралу
.
Заметим, что перед производством вычислений всегда строят качественный вид фигуры, площадь которой необходимо вычислить.
Пример 7.26. Найти площадь фигуры, ограниченной линиями 
, х = 0, у = 4.
Решение. Из чертежа видно, что искомая площадь S криволинейного треугольника ОАВ равна разности двух площадей:
S = S 0 авс – S 0 ВС ,
каждая из которых находится по геометрическому смыслу определенного интеграла.
Решая систему
получаем, что точка В пересечения прямой у = 4 и кривой имеет координаты (2; 4).
Тогда
,
.
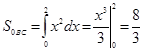Окончательно 
(ед2).
Отметим, что данная задача может быть также решена другим способом, если рассматривать площадь под кривой до оси у. Тогда пределы интегрирования необходимо заменить на отрезок [0; 4], на котором переменная у меняет свои значения:
16/3(ед.2).
Пусть функция у = f (x)неположительная и непрерывна на [ а, b ].
Тогда площадь под осью х вычисляется с учетом неположительности функции у = f (x):
, т.е. 
.
Таким образом, если функция у = f (x) неположительная на [ а, b ],то площадь S над кривой у = f (x)на [ а, b ]отличается з н а к о м определенного интеграла 
.
Пример 7.27. Найти площадь фигуры, ограниченной линиями 
, у = х – 2, у = 0.
Решение. Из рисунка видно, что искомая площадь S криволинейного треугольника 0 АВ может рассматриваться как площадь над ломанной кривой 0 АВ на отрезке [0; 2]. Однако указанная кривая не задается одним уравнением.
Поэтому для нахождения S = S 0 AB разобьем криволинейный треугольник 0 АВ на части, проецируя точку излома А на ось абсцисс. Тогда S = S 0 AC + SABC.
Абсцисса точки А легко определяется, как точка пересечения линий 
и у = х – 2. Ее значение равно 1. Тогда можно записать
;
.
Окончательно 
(ед.2).
Пусть на отрезке [ а, b ]задана непрерывная функция y = f (x)общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция у = f (x) будетзнакопостоянна или равна нулю.
 |
В этом случае площадь заштрихованной фигуры равна алгебраической сумме S = S 1 + S 2 + S 3 соответствующих определенных интегралов:
.
Рассмотрим теорему, применение которой часто упрощает решение задач на вычисление площадей плоских фигур:
пусть на отрезке[ а, b ]заданы непрерывные функции у = f 1(x) и у = f 2(x)такие, что f 2(x) ≥ f 1(x). Тогда площадь S фигуры, заключенной между кривыми y = f 2(x) и y = f 1(x),на отрезке[ а, b ] вычисляется по формуле
. (7.1)
Проиллюстрируем теорему графически. Возможны несколько случаев расположения кривых на отрезке [ а, b ].
1. f 2(x) ≥ f 1(x) ≥ 0.
.
2. 0 ≥ f 2(x) ≥ f 1(x).
3. f 2(x) ≥ 0, f 1(x) 
0.
.
4. 
Общий случай сводится к частным случаям,
рассмотренным выше, если разбить отрезок [ а, b ]на отдельные отрезки [ а, с ],[ с, d ],[ d, b ].
Пример 7.28. Найти площадь фигуры, ограниченной линиями у = х2 – 2, у = х.
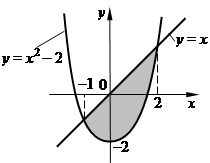Решение. Найдем координаты точек пересечения параболы у = х – 2 и прямой у = х. Решая систему из этих уравнений, получим точки (– 1; –1) и (2; 2).
На интегрируемом отрезке [–1; 2] выполняется х ≥ х 2 – 2. Тогда по формуле (5.1) имеем:
(ед.2).
Пример 7.29.
Найти площадь фигуры, ограниченной линиями у = 4– х 2, у = х 2– 2 х.
Решение. Координаты точек пересечения кривых у = 4 – х 2 и у = х 2 –2 х найдем из системы их уравнений: (–1; 3) и (2; 0).
Проецируя фигуру на ось абсцисс, видно, что интегрируемый отрезок составляет [–1; 2]. На этом на отрезке выполняется f 2(x) = 4 – х 2 ≥ f 1(x) = х 2 – 2 х.
Применяя формулу (5.1), получаем
(ед.2).
Пример 7.30.
Вычислить площадь фигуры, ограниченной графиком функции y = 6 x – x 2 и осью0 x.
Решение. Графиком функции y =6 x – x 2 является квадратичная парабола, повернутая ветвями вниз. Абсциссы точек пересечения графика с осью x находятся из решения уравнения 6 x – x 2 = 0, т. е. x 1 = 0; x 2 = 6. Следовательно, фигура, площадь которой нужно найти, имеет вид, изображенный на рисунке.
Из геометрического смысла определенного интеграла очевидно, что площадь
(ед.2).
Пример 7.31.
Вычислить площадь криволинейной трапеции, ограниченной графиком функции y = ex, осью x, осью y и прямой x = 2.
Решение. Из рисунка следует, что
(ед.2).
Пример 7.32.
Вычислить площадь фигуры, ограниченной графиками функций y = x 2 и
y = x + 2.
Решение. Из рисунка видно, что искомая заштрихованная площадь S равна разности площадей двух криволинейных трапеций, ограниченных с боков линиями x = x 1и x = x 2.Значения x 1и x 2представляют собой абсциссы точек пересечения графиков, которые находим, решая уравнение:
; 
;
; 
; 
; 
.
Искомая площадь S равна
(ед.2).
7.6. Методы вычисления определенного интеграла
Необходимо заметить, что вычисление определенного интеграла производится в два этапа.
На первом этапе вычисляется первообразная, а затем (на втором этапе) в нее подставляются пределы интегрирования по формуле Ньютона-Лейбница.
Методы вычисления первообразной определенного интеграла совершенно аналогичны неопределенному интегрированию.
Однако при использовании методов замены переменной и интегрирования по частям в определенном интеграле имеются свои особенности.
Действительно, если необходимо вычислить
,
в котором f (x) dx можно представить в виде
,
то используется замена переменной t = u (x).
При этом
,
где α = u (a); β = u (b).
Также аналогично вычислению неопределенного интеграла, используя формулу Ньютона-Лейбница, можно получить следующую формулу интегрирования по частям
.
Пример 7.33.
.
Пример 7.34.
.
Пример 7.35.
.
|
Несобственные интегралы
Пусть функция y = f (x) определена и интегрируема на любом отрезке [ a, t ], t > a. Тогда несобственным интеграломс бесконечным верхним пределом называется предел
= 
.
Если этот предел существует и конечен, то указанный несобственный интеграл называется сходящимся и он равен этому пределу.
Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся и его вычисление невозможно.
Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом:
.
Несобственный интеграл с бесконечными пределами 
можно представить как сумму
.
Если оба интеграла в правой части этого равенства являются сходящимися, то и интеграл в левой части сходящийся и он равен сумме этих интегралов. Если хотя бы один из интегралов в правой части расходится, то и результирующий интеграл тоже расходится.
Введем понятие несобственного интеграла с конечными пределами, при приближении к которым функция стремится к бесконечности.
Рассмотрим функцию, неограниченную на отрезке интегрирования.
Пусть 
, как показано на рис. 7.5.
Тогда несобственный интеграл определяется как
,
где 
— бесконечно малая величина. Если предел существует и конечен, то несобственный интеграл сходящийся и он равен этому пределу. Если предел не существует или бесконечен, то несобственный интеграл расходящийся.
Аналогично вводится несобственный интеграл, если 
:
.
Пример 7.38.
.
Пример 7.39.
.
Пример 7.40.
.
Пример 7.41.
