Одним из методов нахождения интегралов, отличных от табличных, является преобразование подынтегральной функции таким образом, чтобы осуществить переход от произведения или частного функций к их сумме и, в конечном итоге, на основе свойств интеграла 4 и 5 свести эти интегралы к табличным.
Такой метод интегрирования называют методом разложения. Часто при этом успех достигается путем применения формул сокращенного умножения, а также тригонометрических формул перехода от произведения (или степени) к сумме.
Пример 7.3.
.
Пример 7.4.
.
Пример 7.5.
.
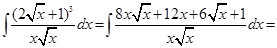
Пример 7.6.
.
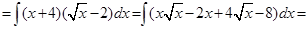
Пример 7.7.
.
Пример 7.8.
.
Метод замены переменной. Если подынтегральное выражение можно представить в виде
,
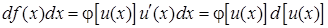а интеграл 
является табличным, то для нахождения интеграла 
производится замена переменной (подстановка)
t = u (x).
Тогда
и легко находится выражение для интеграла через переменную интегрирования t. В заключение необходимо выполнить обратную подстановку, вернувшись к переменной x.
Такая замена переменной позволяет свести сложный интеграл к табличному. Нахождение 
в подынтегральной функции часто называют выделением дифференциала.
Наиболее просто осуществить подстановку, когда u (x) является линейной функцией вида
u (x) = kx + b,
то есть если интеграл имеет вид
.
Действительно, пусть F (x) — первообразная для f (x). Тогда
, d [ u (x)]= kdx и 
.
Следовательно,
.
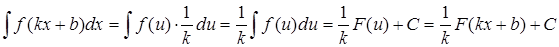Пример 7.9.
Найти неопределенный интеграл 
.
Решение. Используя последнюю формулу, можно сразу записать ответ
.
Рассмотрим этот пример подробнее, используя выделение дифференциала:
.
Следовательно, нужно сделать замену переменной (подстановку) u = 3 x + 2. Запишем
.
Пример 7.10.
.
Обозначим t = cos x. Тогда
.
Пример 7.11.
.
В примере использовалось обозначение t = x 2 + 5.
Необходимо уточнить, что во многих случаях выделить дифференциал достаточно трудно. Поэтому часто метод замены переменной используют, просто пробуя различные подстановки.
Пример 7.12. Рассмотрим последний пример, в котором использовалась подстановка
t = x 2 + 5.
Тогда
; 
; 
и, подставляя в исходный интеграл, имеем
.
Существует несколько типовых приемов при интегрировании методом замены переменной. Рассмотрим некоторые из них.
1. Если нужно найти интеграл от алгебраической дроби, причем в знаменателе дроби находится квадратный трехчлен ax 2 + bx + c, а в числителе — многочлен от x не выше первой степени, то в знаменателе выделяется полный квадрат и новая переменная приравнивается к выражению, возводимому в квадрат.
Тот же прием применяется, если квадратный трехчлен находится под знаком квадратного корня.
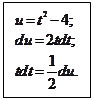
Пример 7.13.
.
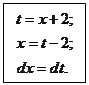Пример 7.14.
.
2. Если в знаменателе дроби подынтегральной функции находится квадратный трехчлен, а в числителе — многочлен от x степени выше первой, то следует провести деление, например, уголком числителя на знаменатель, после чего интеграл сводится к уже рассмотренным случаям.
Пример 7.15.
.
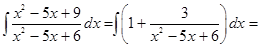
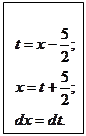
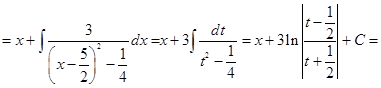
3. Если в подынтегральной функции имеются корни различной степени из x, то часто к успеху приводит замена переменной 
, где n — наименьшее общее кратное показателей степени всех корней.
Пример 7.16.
.
4. Если подынтегральная функция представляет собой тригонометрическое выражение, то часто используют замену переменной 
. Тогда тригонометрические функции запишутся в виде:
; 
;
.
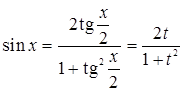Найдем dx. Для этого отразим переменную x
.
И окончательно
.
Пример 7.17.
.
Очень часто на практике является полезным использование следующих формул
;
.
Пример 7.18.
 |  |
Пример 7.19.
Интегрирование по частям. В некоторых случаях интеграл можно представить в виде
.
Если при этом легко вычисляется интеграл 
, то следует воспользоваться формулой, называемой формулой интегрирования по частям
.
Эта формула легко получается при интегрировании дифференциала произведения двух функций. Действительно,
.
Интегрируя, получаем
; 
.
Интегрирование по частям обычно используют тогда, когда подынтегральная функция представляет собой произведение двух функций разного типа (степенной и тригонометрической; степенной и показательной; степенной и логарифмической; тригонометрической и показательной и т. п.).
Если в подынтегральном выражении имеется логарифмическая функция, то ее следует принять за u, а если логарифмической функции в подынтегральном выражении нет, то за u принимают степенную функцию. Все, что остается под интегралом, принимают за dv.
Пример 7.20.
.
Пример 7.21.
.
Не все интегралы могут быть выражены через элементарные функции. Эти интегралы имеют вид:
; 
; 
; 
; 
; 
.
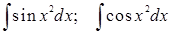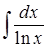Для вычисления таких интегралов (иногда их называют неберущимися) используются специальные методы.
