и экономический смысл
Пусть на отрезке [ a, b ] определена некоторая функция y = f (x) (рис. 13.1). Разобьем отрезок [ a, b ] на n частей точками x 1 , x 2 ,…, xn –1 . Для унификации обозначений положим a = x 0 ; b = xn.
Отрезок [ xk –1 , xk ] назовем k -тым частичным отрезком. Длина k -того частичного отрезка равна
xk = xk – xk –1 .
Число d равное наибольшей длине k -того частичного отрезка называется диаметром или мелкостью разбиения
.
Выберем на каждом частичном отрезке [ xk –1 , xk ] произвольную точку 
k, найдем f (
k) и составим сумму
.
Функция 
называется интегральной суммой для функции f (x) на отрезке [ a, b ]. Ясно, что таких интегральных сумм можно составить бесконечное множество.
Если существует предел интегральных сумм при 
(при этом 
), то он называется определенным интегралом от функции f (x) в пределах от a до b, а функция f (x) называется интегрируемой на отрезке [ a, b ].
Эту формулу можно записать в виде:
.
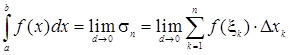Числа a и b называются соответственно нижним и верхним пределами интегрирования, а функция f (x), как и в случае неопределенного интеграла, называется подынтегральной функцией.
Отметим, что в отличие от неопределенного интеграла, представляющего собой множество функций, определенный интеграл — это вполне определенное число.
Геометрический смысл определенного интеграла. Как видно из рис. 7.1, интегральная сумма
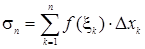
численно равна площади заштрихованной ступенчатой фигуры.
При переходе к пределу при интегральная сумма по определению будет равна интегралу 
, а ступенчатая линия, ограничивающая сверху заштрихованные прямоугольники, совпадет с графиком функции y = f (x) на отрезке [ a, b ].
 |
Рис. 7.1. Разбиение площади под кривой функции y = f (x)
Следовательно, геометрический смысл определенного интеграла состоит в том, что он по абсолютной величине численно равен площади фигуры (криволинейной трапеции), ограниченной графиком функции y = f (x), осью x и прямыми x = a и x = b (рис. 7.2).
 |
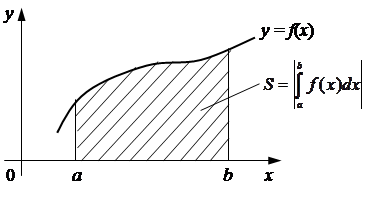Рис. 7.2. Геометрический смысл определенного интеграла
Символ абсолютной величины здесь используется потому, что площадь фигуры является величиной положительной, а определенный интеграл может быть отрицательным числом, если, например, f (x) < 0 на отрезке [ a, b ] или если при положительной f (x) верхний предел интегрирования меньше нижнего.
Экономический смысл определенного интеграла состоит в том, что если подынтегральная функция является предельной величиной (т. е. производной) какого-либо экономического показателя, то определенный интеграл представляет собой соответствующую этому показателю суммарную величину.
Например, пусть известна производительность труда как функция времени f (t). Из курса экономики известно, что производительность труда представляет собой предельный объем произведенной продукции (т. е. производную объема произведенной продукции по времени). Тогда объем V продукции, произведенной от момента времени t 1 до момента t 2, равен определенному интегралу
.
