Преобразование звезды в треугольник и треугольника в звезду.

Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.15), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.16), - треугольником. В узлах 1, 2, 3 (потенциалы их φ_1, φ₂ и φ₃) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).

Обозначим токи, подтекающие к узлам 1, 2, 3 через I₁, I₂ и I₃.

Часто при расчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены.

Рис.2.15 Рис.2.16

Выведем формулы преобразований. С этой целью выразим токи I₁ I₂ и I₃ в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

Для звезды

'(2.25)

Но

(2.26)

Подставим (2.26) в (2.25) и найдем φ₀:

откуда

(2.27)

Введем φ₀ в выражение (2.26) для тока I₁:

(2.28)

Для треугольника в соответствии с обозначениями на рис. 2.16

(2.29)

Так как ток I, в схеме рис. 2.15 равен току I, в схеме рис. 2.16 при любых значениях потенциалов φ_1, φ₂ и φ_3, то коэффициент при φ₂ в правой части (2.27) равен коэффициенту при φ₂ в правой части (2.26), а коэффициент при φ₃ в правой части (2.27) - коэффициенту при φ₃ в правой части (2.26).

Следовательно,

(2.30)

(2.31)

Аналогично

(2.32)

Формулы (2.30)-(2.32) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе - сумма проводимостей лучей звезды.

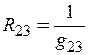Из уравнений (2.30)-(2.32) выразим сопротивления лучей звезды ; и через сопротивления сторон треугольника: ; и

С этой целью запишем дроби, обратные (2.30)-(2.32):

(2.33)

где

(2.34)

(2.35)

(2.36)

Подставив (2.33), (2.35), и (2.36) в (2.34), поучим:

Следовательно,

Подставив m в (2.35), найдем

. (2.37)

Аналогично

; (2.38)

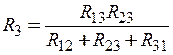. (2.39)

Структура формул (2.37)-(2.39) аналогична структуре формул (2.30)-(2.32).

Преобразование треугольника в звезду можно пояснить, рассмотрев, например, рис. 2.17 а, б. Схема до преобразования изображена на рис. 2.17 а, штриховой линией обведен преобразуемый треугольник. На рис. 2.17 б представлена та же схема после преобразования. Расчет токов произвести для нее проще (например, методом двух узлов), чем для схемы на рис. 2.17 а.

В полезности преобразования звезды в треугольник можно убедиться на примере рис. 2.17 в,г. Схема до преобразования изображена на рис. 2.17 в, штриховой линией обведена преобразуемая в треугольник звезда. На рис. 2.17 г представлена схема после преобразования, которая свелась к последовательному соединению сопротивлений.

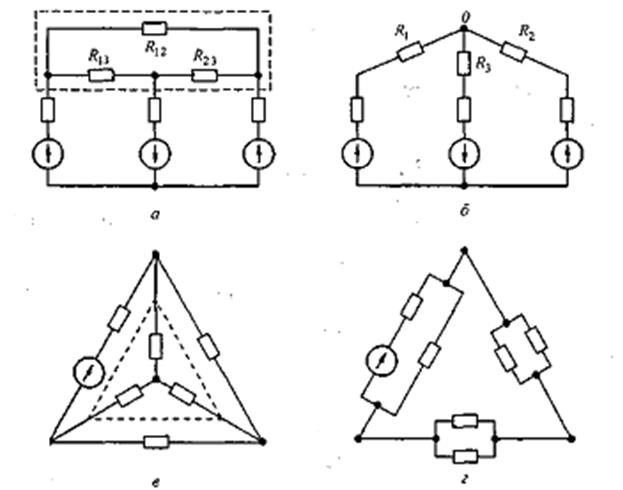
Рис.2.17