Принцип наложения и метод наложения.

ГЛАВА2

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Основные методы расчета электрических цепей.

Метод контурных токов.

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.

Таким образом, метод контурных токов можно определить как ме­тод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.

Следовательно, метод контурных токов более экономен при вычисли-тельной работе, чем метод на основе законов Кирхгофа (в нем меньше число уравнений).

 

 

 

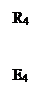
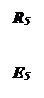
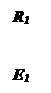
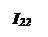
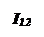
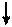
Рис.2.8.

 

Вывод основных расчетных уравнений приведем применительно к схеме с двумя независимыми контурами (рис. 2.8). Положим, что в левом контуре по часовой стрелке течет контурный ток I₁₁, а в правой (также по часовой стрелке) - контурный ток I₂₂. Для каждого контура составим уравнения по второму закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением R₅) течет сверху вниз ток I₁₁-I₂₂ . Направления обхода контуров примем также по часовой стрелке.

Для первого контура

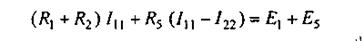(2.6)

или

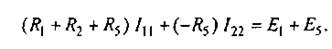(2.7)

Для второго контура

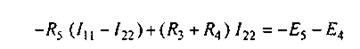
или

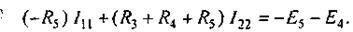
В уравнении (2.12) множитель при токе I₁₁, являющийся суммой сопротивлений первого контура, обозначим через R₁₁, множитель при токе I₂₂ (сопротивление смежной ветви, взятое со знаком минус) — через R₁₂.

Перепишем эти уравнения следующим образом:

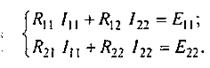(2.8)

Здесь

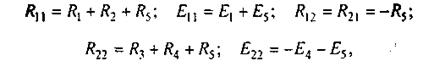
где R₁₁ - полное, или собственное, сопротивление первого контура; R₁₂ - сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; E₁₁ - контурная ЭДС первого контура, равная алгебраической сумме ЭДС этого контура (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура); R₂₂ - полное, или собственное, сопротивление второго контура; R₂₁ - сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; E₂₂ - контурная ЭДС второго контура.

В общем случае можно сказать, что сопротивление смежной ветви между k- и m- контурами (R_km) входит в уравнение со знаком минус, если направления контурных токов I_kkIl_mm вдоль этой ветви встречны, и со знаком плюс, если направления этих токов согласны.

Если в схеме больше двух контуров, например три, то система урав-нений выглядит следующим образом:

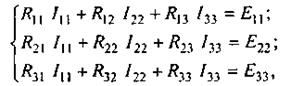(2.9)

илив матричной форме

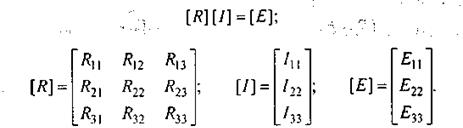(2.10)

Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например по часовой стрелке.

В результате решения системы уравнений какой-либо один или несколько контурных токов могут оказаться отрицательными.

В ветвях, не являющихся смежными между соседними контурами (например, в ветви с сопротивлениями R₁, R₂ на рис. 2.8), найденный контурный ток является действительным током ветви. В смежных ветвях через контурные токи определяют токи ветвей. Например, в ветви с сопротивлением R₅ протекающий сверху вниз ток равен разности I₁₁ -I₂₂

Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно п.

Общее решение системы п уравнений относительно тока I_kk:

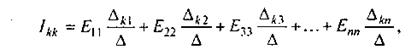(2.11)

где

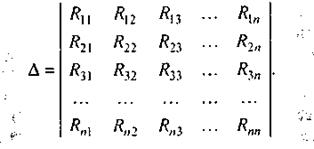(2.12)

есть определитель системы.

Алгебраическое дополнение D_km получено из определителя D путем вычеркивания k-го столбца и т-й строки и умножения полученного оп-ределителя на (-1)^k+m.

Если из левого верхнего угла определителя провести диагональ в его правый нижний угол (главная диагональ) и учесть, что R_km = R_mk, то можно убедиться в том, что определитель делится на две части, являющиеся зеркальным отображением одна другой. Это свойство определителя называют симметрией относительно главной диагонали. В силу симметрии определителя относительно главной диагонали D_кт = D_тк.

 

Принцип наложения и метод наложения.

Чтобы составить общее выражение для тока в k -ветви сложной схемы, составим уравнения по методу контурных токов, выбрав контуры так, чтобы k -ветвь входила только в один k -контур (это всегда возможно). Тогда согласно (2.11) ток в k -ветви будет равен контурному току I_kk. Каждое слагаемое пра-вой части (2.11) представляет собой ток, вызванный в k -ветви соответст-вующей контурной ЭДС. Например, Е₁₁ Δ _ki / Δ есть составляющая тока k -ветви, вызванная контурной ЭДС Е₁₁. Каждую из контурных ЭДС можно выразить через ЭДС ветвей Е₁, Е₂, Е₃,..., Е_к..., Е_n, сгруппировать коэффициенты при этих ЭДС и получить выражение следующего вида:

I_k = Е₁ g _k1 + Е₂ g _k2 + Е₃ g _k3 +…..+ Е_k g _kk + Е_n g _nn (2.13)

Если контуры выбраны таким образом, что какая-либо из ЭДС, напри-мер Е_т, входит только в один m -контур, а в другие контуры не входит, то

g _{km =} Δ _km / Δ.

Уравнение (2.18) выражает собой принцип наложения.

Принцип наложения формулируется следующим образом: ток в k-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных элек-трических цепей.

При расчете цепей данным методом поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов.