Расчет сложных схем упрощается при замене нескольких параллельно включенных ветвей, содержащих источники ЭДС, источники тока и сопротивления, одной эквивалентной ветвью.
Участок цепи на рис. 6 эквивалентен участку цепи на рис. а, если при любых значениях тока I, подтекающего из всей остальной, не показанной на рисунке части схемы, напряжение на зажимах а и b (Uab) 
а б в
Рис.2.13
в обеих схемах одинаково. Для того чтобы выяснить, чему равняются Rэ и E, составим уравнения для обеих схем.
Для схемы на рис.2.13 а
но
(2.19)
Следовательно,
(2.20)
где п - число параллельных ветвей с источниками ЭДС; q - число па-раллельных ветвей с источниками тока. Для схемы на рис.2.21, б
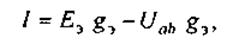(2.21)
где 
Равенство токов в схемах (см. рис.2.13 а,б) должно иметь место при любых значениях Uab, а это возможно только в том случае, когда коэффициент при Uab (2.21) равен коэффициенту при Uab в (2.20).
Следовательно,
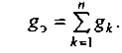(2.22)
Если слагаемые с Uab в (2.20) и (2.21) равны и токи I по условию эквивалентности двух схем также равны, то
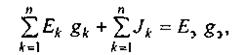
откуда
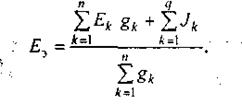(2.23)
Формула (2.22) дает возможность найти проводимость gэ и по ней Rэ в схеме на рис.2.13, б. Из этой формулы видно, что проводимость gэ не зависит от того, есть в ветвях схемы (рис.2.13 а) ЭДС или нет.
При подсчетах по формуле (2.23) следует иметь в виду следующее:
1) если в какой-либо ветви схемы ЭДС отсутствует, то соответствующее слагаемое в числителе (2.23) выпадает, но проводимость этой ветви в знаменателе (2.23) остается;
2)если какая-либо ЭДС в исходной схеме имеет направление, обратное изображенному на рис.2.13 а, то соответствующее слагаемое войдет в числитель формулы (2.23) со знаком минус.
Ветви схемы (рис.2.13 а, б) эквивалентны только в смысле поведения их по отношению ко всей остальной части схемы, не показанной на рисунке, но они не эквивалентны в отношении мощности, выделяющейся в них.
Метод двух узлов.
Часто встречаются схемы, содержащие всего два узла (рис. 2.14). Наиболее рациональным методом расчета токов в них является метод двух узлов.
Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы.
Расчетные формулы этого метода получают на основе формул (2.20) и (2.29); их также можно просто получить из более общего метода - метода узловых потенциалов.
Рис.2.14
В отличие от схемы на рис. 2.13, а ток I к узлам а и b схемы на рис. 2.14 не подтекает.
Поэтому если в формуле (2.20) принять I = 0, то из нее может быть найдено напряжение между двумя узлами:
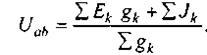(2.24)
После определения напряжения Uab находят ток в любой (А-й)ветви по формуле 
