Связь поверхностных интегралов первого и второго рода.
Поверхностные интегралы первого и второго рода связаны друг с другом соотношением:

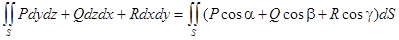
В этой формуле cosa, cosb, cosg - направляющие косинусы нормали к поверхности S в выбранную сторону поверхности.
Формула Гаусса – Остроградского.
Формула Гаусса – Остроградского является аналогом формулы Грина – Остроградского. Эта формула связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью.
Для вывода формулы Гаусса – Остроградского надо воспользоваться рассуждениями, подобными тем, которые использовались при нахождении формулы Грина – Остроградского.
Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум доугим координатным осям.
После этого полученные результаты обобщаются, приводя к формуле Гаусса – Остроградского:


Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.
На практике формулу Гаусса – Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
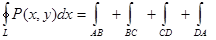
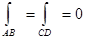


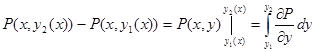
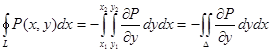
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:

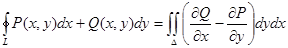
Эта формула называется формулой Остроградского – Грина.
Формула Остроградского – Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область D все время оставалась по левую сторону линии обхода.
Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.
Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.
Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.
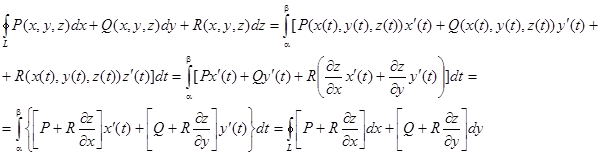
Введем обозначения: 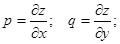
Применив формулу Грина – Остроградского, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:
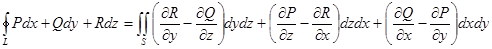
эта формула и называется формула Стокса.






