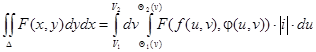Теорема. Егер (P) облысында анықталған f(x,y) функциясы үшін 
қос интегралы бар болса және a 
x b интервалындағы х – тің әрбір тұрақты мәнінде жай интеграл
, (a x b) бар болса, онда сонымен қатар қайталанған интеграл
бар болады және 
теңдік орындалатын болады.Х және у айнымалыларының рольдерін өзгерте отырып осы формуламен қатар мына формула орындалады
және 
ДӘРІС. Қос интегралдарда айнымалыларды ауыстыру
Жазық облыстарды түрлендіру. Біреу х және утік бұрышты осьтеріне, ал екіншісі сондай 
және 
осьтеріне қатысты алынған екі жазықтық берілген дейік. Осы жазықтықтардағы шектелген екі тұйық облысты қарастырамыз. Мынадай қос интегралды қарастырамыз: ху жазықтықтағы (D) облысыын және облысында 
облысын. Бұл облыстардың әрқасысының контуры немесе шекарасы жай үзінді тегіс қисық деп ұйғарамыз. (D) облысыын контурын (S) символымен және облысының контурын 
символымен белгілейміз.
облысында үздіксіз функциялар системасы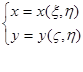 
(1)
берілген дейік. Бұл система облысының әрбір (, ) нүктесіне (D) облысынын бір белгілі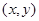 
нүктесін сәйкес және де (D) облысынын бір нүктесі деп қалып қоймайды, сондықтан бұл облыстын әрбір нүктесі облысының кемінде бір (, ) нүктесіне сәйкес келетін болады.
Егер әртүрлі (, ) нүктелерге әр түрлі 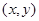нүктелері сәйкес келетін болса, онда әрбір 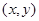нүктесі тек бір ғана (, ) нүктесіне сәйкес келеді, ендеше (1) теңдеулер және ға қатысты бір мәнді шешілген болады және айнымалылары (D) облысында х,у тердіңбір мәнді функциялар болады
(2). Сөйтіп (D) және облыстарының арасында өз ара бір мәнді немесе бір бір мәнді сәйкестік тағайындалады. Сонымен қатар (1) формулалар облысын (D) облысына түрлендіреді, ал (2) формулалар (D) облысын облысына керісінше түрлендіреді деп те айтады. Бұл жағдайда қажетті түрде контурының нүктелеріне (S) контурының нүктелері сәйкес келетіндігін және керісінше болатындығын ескертеміз. Одан әрі (1) функциялар үздіксіз ғана болып қоймай, облысында үздіксіз бірінші ретті дербес туындылары болады деп ұйғарамыз. Сонда функцияоналдық анықтауыш та 
(3)
облысында (, ) лардың үздіксіз функциясы болады. Бұл анықтауыш әрқашан 0 ге тең емес деп есептейміз, ал ендеше үздіксіз болғандықтан тұрақты таңбасын сақтайтын болады.
, мұнда (D) облысы қарапайым үзінді тегіс (S) контурымен қоршалған, ал f(x,y) функциясы осы облыста үздіксіз. D облысы {a<х<b, j1(x)<y<j2(х)}.
Енді х = f(u, v); y = j(u, v) болсын. Сонда қисық сызықты координатталар системасында (D) фигураның ауданын өрнектейтін формуланы барлық шарттар орындалған деп есептейміз.
Онда dx =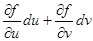 
; dy = 
;
өйткені х айнымалы тұрықты болғандықтан dx = 0.
Мына өрнекті 
, яғни 
Жоғарғы теңдеуге қойғанда dy, ті аламыз:
Якобиан деп аталады f(u, v) және j(u, v) функцияларға
Онда 
Егер интегралдау ретін өзгертесек онда
