ДӘРІС. Бірінші ЖӘНЕ ЕКІНШІ типті беттік интегралДАРЫ

 

Үзінді тегіс контурмен қоршалған кейбір екі жақты тегіс S бетің нүктелірінде f(M) функциясы анықталған болсын. S бетті қалауымызша жүргізілген қисықтыр торы арқылы бөліктерге бөлеміз. Әрбір бөліктен қалауымызша нүктесін алып,сол нүктедегі функцияның f(M ) мәнін есептейміз және оны беттің сәйкес бөлігінің ауданына көбейтіп, барлық осындай көбейтінділердің қосындысын құрамыз Бұл қосынды бұдан бұрын қарастырылған көп қосындыларға ұқсас болғандықтын, біз оны интегралдық қосынды деп атайтын боламыз.

Анықтама. Барлық бөліктердін диаметрлері нөльге ұмтылғандығы осы косындының шектеулі шегін f(M) функциясының S бет бойындағы алынған беттік интеграл деп аталады. Және

 

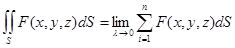
символмен белгіленеді

Беттік интегралдың қасиеттері:

 

1) S – ауданы

2)

3)

4) Егер S бетті екі бетке бөлсек S₁ және S₂, онда

5) Егер , онда

6)

Беттік интегралды екі еселі интегралға келтіру

 

Сөйтіп бірінші типті беттік интегралды еселі интегралға кнлтіру үшін x, z, y координатталарын олардың параметрлер арқылы өрнектерімен, ал ауданның dS элементін оның қисық сызықты координаталар арқылы өрнегімен ауыстырса болғаны

Если на поверхности S есть хотя бы одна точка и хотя бы один не пересекающий границу поверхности контур, при обходе по которому направление нормали в точке меняется на противоположное, то такая поверхность называется односторонней.

Если при этих условиях направление нормали не меняется, то поверхность называется двухсторонней.

Будем считать положительным направлением обхода контура L, принадлежащего поверхности, такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остается слева.

Двухсторонняя поверхность с установленным положительным направлением обхода называется ориентированной поверхностью.

 

Рассмотрим в пространстве XYZ ограниченную двухстороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан либо уравнением вида z = f(x, y), либо является цилиндрической поверхностью с образующими, параллельными оси OZ.

Определение. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы, составленные как суммы произведений значений некоторой функции на площадь частичной поверхности, имеют конечный предел, то этот предел называется поверхностным интегралом второго рода.

 

- поверхностный интеграл второго рода.

 

Свойства поверхностного интеграла второго рода аналогичны уже рассмотренным нами свойствам поверхностного интеграла первого рода.

Т.е. любой поверхностный интеграл второго рода меняет знак при перемене стороны поверхности, постоянный множитель можно выносить за знак интеграла, поверхностный интеграл от суммы двух и более функций равен сумме поверхностных интегралов от этих функций, если поверхность разбита на конечное число частичных поверхностей, интеграл по всей поверхности равен сумме интегралов по частичным поверхностям.

Если S- цилиндрическая поверхность с образующими, параллельными оси OZ, то . В случае, если образующие поверхности параллельны осям OX и OY, то равны нулю соответствующие составляющие поверхностного интеграла второго рода.

Вычисление поверхностного интеграла второго рода сводится к вычислению соответствующих двойных интегралов. Рассмотрим это на примере.