Наклавши ґрати на аркуш паперу, вписуємо перші п’ятнадцать (за кількістю вирізів) літер повідомлення:
ШИФРРЕШЕТКАЯВЛЯ …
Знявши ґрати, ми побачимо текст, поданий на рис. 5.2. Повернімо ґрати на 180°. У „віконечках” з'являться нові, ще не заповнені клітинки. Вписуємо в них наступні п'ятнадцять літер. Вийде запис, наведений на рис. 5.3. Потім повертаємо ґрати на інший бік і зашифровуємо залишок тексту в аналогічний спосіб (рис. 5.4 та 5.5).
| Ш | Е | Ш | Т | С | Я | |||||||||||||||
| И | Ф | Р | Р | И | Ф | Р | Р | Ч | ||||||||||||
| Е | Ш | Е | Е | А | Ш | С | Е | |||||||||||||
| Т | К | Т | Т | Н | К | Ы | ||||||||||||||
| А | А | М | С | Л | У | |||||||||||||||
| Я | В | Л | Я | Я | В | Л | Ч | Я |
Рисунок 5.2 Рисунок 5.3
| Е | Ш | А | Т | С | Е | М | Я | Ш | Е | Ш | А | Т | С | Е | М | Я | Н | Ш | ||
| И | И | Ф | Р | Р | Ч | И | И | О | Й | Ф | П | Р | Р | Ч | Е | |||||
| Е | А | Ф | Ш | С | Р | Е | Р | Е | А | Ф | Е | Ш | С | Р | С | Е | ||||
| Т | А | Т | Н | М | К | Ы | А | Т | А | Т | Т | Н | М | А | К | Ы | А | |||
| Р | А | М | С | Ш | Л | Р | У | У | Р | А | М | С | Ш | Л | Р | У | Н | У | ||
| Т | Я | В | Л | Ч | Я | О | Т | Я | В | К | В | Л | И | Ч | Я |
Рисунок 5.4 Рисунок 5.5
Одержувач повідомлення, котрий має точно такі самі ґрати, без утруднень прочитає вихідний текст, накладаючи ґрати на шифртекст по порядку у чотири способи.
Можна довести, що кількість можливих трафаретів, тобто кількість ключів шифру "ґрати", становить T = 4 mk. Цей шифр призначено для повідомлень довжини n = 4 mk. Кількість всіх переставлянь у тексті такої довжини становитиме (4 mk)!, що в багато разів більше за кількість Т. Однак вже при розмірі трафарету 8´8 кількість можливих ґрат перевершує чотири мільярди.
5.2 Приклади розв’язування криптографічних завдань за
допомогою шифрів простої заміни
Шифри заміни схарактеризовуються тим, що окремі частини повідомлення (літери, слова тощо) замінюються на певні інші літери, числа, символи і т. д. При цьому заміна здійснюється у такий спосіб, аби потім за шифрованим повідомленням можна було однозначно відновити передаване повідомлення.
5.2.1 Шифрування одноабетковою підстановкою
Нехай зашифровується повідомлення українською мовою й при цьому заміні підлягає кожна літера повідомлення. Формально в цьому разі шифр заміни можна описати в такий спосіб. Для кожної літери а вихідної абетки будується певна множина символів Ма,аби множини Ма та Мв попарно не перетинались за а ≠ в, тобто будь-які дві різні множини не містили однакових елементів. Множина Ма називається множиною шифропозначань для літери а.
Таблиця 5.1 є ключем шифру заміни. Знаючи її, можна здійснювати як зашифровування, так і розшифровування.
Таблиця 5.1- Зашифровування літер відкритого повідомлення за допомогою будь-якого символу з множини Мj
| а | б | в | … | я |
| Ма | Мб | Мв | … | Мя |
При зашифровуванні кожна літера а відкритого повідомлення, розпочинаючи з першої, замінюється на будь-який символ з множини Ма . Якщо в повідомленні міститься кілька літер а, то кожна з них замінюється на будь-який символ з Ма. За рахунок цього за допомогою одного ключа (табл. 5.2) можна дістати різноманітні варианти зашифрованого повідомлення для одного й того самого відкритого повідомлення.
Наприклад, якщо ключем є таблиця 5.2, то повідомлення «мені відомі шифри заміни» може бути зашифровано, кожним з трьох способів, поданих в цій таблиці.
Таблиця 5.2 - Зашифровування літер відкритого повідомлення за допомогою одного з трьох числових символів множини Мj
| а | б | в | г | д | е | є | ж | з | и | і | к | л | м | н | о | п |
| р | с | т | у | ф | х | ц | ч | ш | щ | ь | ї | ю | я |
м е н і в і д о м і ш и ф р и з а м і н и
Оскільки множини Ма, Мб, Мв, …, Мя попарно не перетинаються, то за кожним символом шифрованого повідомлення можна однозначно визначити, якій множині він належить й, отже, яку саме літеру відкритого повідомлення він замінює. Тому розшифровування є можливе й відкрите повідомлення визначається у єдиний спосіб.
5.2.2 Шифрування за допомогою квадрата Полібія
Як вже зазначалося вище, за один з перших шифрів простої заміни вважається так званий полібіанський квадрат. За два сторіччя до нашої ери Полібій винайшов для цілей зашифровування квадратну таблицю розміром 5´5, заповнену літерами грецької абетки у довільному порядку (рис. 5.6).
| λ | ε | υ | ω | γ |
| ρ | ζ | δ | σ | ο |
| μ | η | β | ξ | τ |
| ψ | π | θ | α | ς |
| χ | ν | - | φ | ί |
Рисунок 5.6 – Полібіанський квадрат, заповнений у довільний спосіб
24-ма літерами грецької абетки й прогалиною
При зашифровуванні в цьому квадраті відшукували чергову літеру відкритого тексту й записували до шифртексту літеру, розташовану нижче за неї в тім самім стовпці. Якщо літера тексту містилася в нижньому рядку таблиці, то для шифртексту брали найверхню літеру з того самого стовпця. Наприклад, для слова
τ α υ ρ ο σ χ
виходить шифртекст
ς φ δ μ τ ξ λ.
Концепція полібіанського квадрата виявилася плідною і набула застосування в криптосистемах подальшого часу.
5.2.3 Зашифровування за рахунок перетворювання числового повідомлення на літерне
Розглянемо 30-літерну абетку української мови:
АБВГДЕЄЖЗИІКЛМНОПРСТУФХЦЧШЩЬЮЯ
У цій абетці відсутні літери Ї, Й, що практично не обмежує можливостей за складання відкритих повідомлень українською мовою.
В абетці будь-якої природної мови літери слідують одна за одною у певному порядку. Це дає можливість надати кожній літері абетки її природний порядковий номер.
Занумеруємо літери української абетки відповідно до табл. 5.3.
Таблиця 5.3 - Відповідність поміж українською абеткою та множиною цілих
| А | Б | В | Г | Д | Е | Є | Ж | З | И | І | К | Л | М | Н |
| О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я |
Якщо у відкритому повідомленні кожну літеру замінити на її природний порядковий номер у розглядуваній абетці, то перетворення числового повідомлення на літерне дозволяє однозначно відновити вихідне відкрите повідомлення. Наприклад, числове повідомлення 1 13 22 1 3 11 20 перетвориться на літерне повідомлення: АЛФАВІТ.
5.2.4 Розшифровування повідомлення за відомою умовою шифрування
Для зашифрованого повідомлення з n літер обирається ключ К – певна послідовність з n літер абетки, наведеної в табл. 5.3. Зашифровування кожної літери повідомлення полягає в додаванні її номера в таблиці з номером відповідної літери ключової послідовності й заміні дістаної суми на літеру абетки, номер якої має ту саму остачу від ділення на 30, що й ця сума.
Необхідно прочитати шифроване повідомлення: РБЬНПТИТСРРЕЗОХ, якщо відомо, що шифрувальна послідовність не містила жодних літер, окрім А, Б та В.
Кожну літеру шифрованого повідомлення розшифруємо в трьох варіантах, припускаючи послідовно, що відповідна літера шифрувальної послідовності є літера А, Б чи В:
Таблиця 5.4 - Три варианти розшифровування шифрованого повідомлення
| Шифртекст | Р | Б | Ь | Н | П | Т | И | Т | С | Р | Р | Е | З | О | Х |
| Варіант А | П | А | Щ | М | О | С | З | С | Р | П | П | Д | Ж | Н | Ф |
| Варіант Б | О | Я | Ш | Л | Н | Р | Ж | Р | П | О | О | Г | Е | М | У |
| Варіант В | Н | Ю | Ч | К | М | П | Е | П | О | Н | Н | В | Д | Л | Т |
Обираючи з кожного стовпчика таблиці 5.4 лише по одній літері, віднайдемо осмислене повідомлення НАШКОРЕСПОНДЕНТ, яке й є шуканим.
Зауваження. З дістаної таблиці можна було б віднайти не одне осмислене повідомлення. Кількість решти різноманітних варіантів вихідних повідомлень без обмежень на осмисленість дорівнює 315, або 14348907, тобто понад 14 мільйонів!
5.2.5 Подвійне шифрування
Перетворення шифру простої заміни в абетці А = { а 1, а 2, …, аn }, яка складається з n різних літер, полягає в заміні кожної літери тексту, який треба зашифрувати, літерою тієї самої абетки, причому різні літери замінюються на різні. Ключем до шифру простої заміни є таблиця 5.5, в якій зазначено, якою саме літерою треба замінити кожну літеру російської абетки А.
Таблиця 5.5 - Зашифровування літер за допомогою шифру простої заміни
| А | Б | В | Г | Д | Е | Ж | З | И | К | Л | М | Н | О | П |
| Ч | Я | Ю | Э | Ы | Ь | Щ | Ш | Ц | Х | Ф | У | Б | Д | Т |
| Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ы | Э | Ю | Я |
| З | В | Р | П | М | Л | К | А | И | О | Ж | Е | С | Г | Н |
Якщо слово СРОЧНО зашифрувати простою заміною за допомогою ключа таблиці 5.5, то вийде слово ВЗДАБД. Зашифрувавши здобуте слово за допомогою того самого ключа вдруге, здобудемо слово ЮШЫЧЯЫ.
Слід визначити, скільки всього всіляких слів можна здобути, якщо зазначений процес зашифровування продовжувати необмежено. Оскільки розглядуваний шифр має таку властивість, що різні літери замінюються на різні, то при зашифровуванні різних слів виходять різні слова. З іншого боку, однакові літери замінюються на однакові незалежно від циклу зашифровування, тому що використовується один і той самий ключ. Отже, при зашифровуванні однакових слів виходять однакові слова, тобто, кількість різних слів, які можна здобути в зазначеному процесі зашифровування з початковим словом СРОЧНО, збігається з найменшим номером циклу зашифровування, котрий дає це початкове слово.
Оскільки літера С повторюється в кожнім циклі зашифровування, номер якого дорівнює 5, а літери Р, О, Ч, Н – у кожнім циклі, номери яких є кратні до 13, 7, 2 та 3 відповідно, то слово СРОЧНО з'явиться вперше в циклі з номером, дорівнюваним
НСК (2,3,5,7,13) = 2 · 3 · 5· 7· 13 = 2730,
де НСК – найменше спільне кратне.
5.2.6 Шифрування за допомогою афінної системи
У системі шифрування Цезаря використовувалися лише адитивні властивості цілих 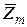 . Однак символи множини
. Однак символи множини 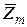 можна також перемножувати за модулем m. Застосовуючи водночас операції додавання та множення за модулем m над елементами множини
можна також перемножувати за модулем m. Застосовуючи водночас операції додавання та множення за модулем m над елементами множини 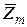 , можна здобути систему підставляння, що її називають афінною системою підставляння Цезаря.
, можна здобути систему підставляння, що її називають афінною системою підставляння Цезаря.
Визначимо перетворювання в такій системі:
Е а,b: 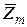 →
→  ,
,
Е а,b: t → Е а,b(t),
Е а,b(t) = at + b (mod m),
де a, b – цілі числа, 0 ≤ a, b < m, НСД (найбільший спільний дільник) (a, m) = 1.
У даному перетворюванні літера, котра відповідає числу t, замінюється на літеру, котра відповідає числовому значенню at + b за модулем m.
Слід зауважити, що перетворення Еа,b(t) є взаємно однозначним відбиттям на множину  лише в тому разі, якщо найбільший спільний дільник чисел a та m дорівнює одиниці, тобто a та m повинні бути взаємно простими числами. Наприклад, нехай m = 26, a = 3, b = 5. НСД (3,26) = 1 і можна здобути таку відповідність поміж числовими кодами літер:
лише в тому разі, якщо найбільший спільний дільник чисел a та m дорівнює одиниці, тобто a та m повинні бути взаємно простими числами. Наприклад, нехай m = 26, a = 3, b = 5. НСД (3,26) = 1 і можна здобути таку відповідність поміж числовими кодами літер:
Таблиця 5.6 - Відповідність поміж числовими кодами літер
| t | |||||||||||||
| 3 t + 5 |
| t | |||||||||||||
| 3 t + 5 |
Якщо перетворити числа на літери англійської мови, дістанемо таку відповідність для літер відкритого тексту та шифртексту:
Таблиця 5.7 - Відповідність для літер англійської мови відкритого тексту та шифртексту
| А | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| F | I | L | O | R | U | X | A | D | G | J | M | P | S | V |
| P | Q | R | S | T | U | V | W | X | Y | Z |
| Y | B | E | H | K | N | Q | T | W | Z | C |
Вихідне повідомлення HOPE перетвориться на шифртекст AVYR.
Достоїнством афінної системи є зручне керування ключами: ключі зашифровування й розшифровування подаються в компактній формі у вигляді пари чисел (a, b). Недоліки афінної системи є аналогічні до недоліків системи шифрування Цезаря.
5.2.7 Шифрування за допомогою системи Цезаря з ключовим словом
Система шифрування Цезаря з ключовим словом є одноабетковою системою підставляння. Особливістю цієї системи є використання ключового слова для зсунення та змінювання порядку символів в абетці підставляння.
Оберемо певне число k, 0  k < 25, і слово чи коротку фразу як ключове слово. Бажано, щоб усі літери ключового слова були різні. Оберемо слово DІPLOMAT за ключове й число k = 5.
k < 25, і слово чи коротку фразу як ключове слово. Бажано, щоб усі літери ключового слова були різні. Оберемо слово DІPLOMAT за ключове й число k = 5.
Ключове слово записується під літерами абетки, розпочинаючи з літери, числовий код якої збігається з обраним числом k:
0 1 2 3 4 5 10 15 20 25
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
D I P L O M A T
Решта літер абетки підставляння записуються після ключового слова за абеткою:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
V W X Y Z D I P L O M A T B C E F G H J K N Q R S U
Тепер ми маємо підставляння для кожної літери довільного повідомлення.
Вихідне повідомлення
SEND MORE MONEY
шифрується як
HZBY TCGZ TCBZS
Слід зазначити, що вимога щодо розходження всіх літер ключового слова не є обов'язковою. Можна просто записати ключове слово (чи фразу) без повторення однакових літер. Наприклад, ключова фраза
КАК ДЫМ ОТЕЧЕСТВА НАМ СЛАДОК И ПРИЯТЕН
і число k = 3 породжують таку таблицю підставляння:
Таблиця 5.8 - Зашифровування літер за допомогою ключової фрази у шифрі простої заміни
| А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П |
| Ъ | Э | Ю | К | А | Д | Ы | М | О | Т | Е | Ч | С | В | Н | Л |
| Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ы | Ъ | Э | Ю | Я |
| И | П | Р | Я | Б | Г | Ж | З | Й | У | Ф | Х | Ц | Ш | Щ | Ь |
Безперечним достоїнством системи Цезаря з ключовим словом є те, що кількість можливих ключових слів є практично невичерпна. Недоліком цієї системи є можливість зламу шифртексту на підставі аналізу частості з׳явлення літер.
5.2.8 Шифрування за допомогою таблиці Трисемуса
Для здобуття шифру заміни Трисемуса зазвичай використовувалися таблиці для записування літер абетки й ключове слово. У таблицю спочатку вписувалося по рядках ключове слово, причому повторювані літери відкидалися. Потім ця таблиця доповнювалася літерами абетки, які не увійшли до неї одна за одною.
Для української абетки таблиця Трисемуса може мати розмір 4´8. Оберемо за ключ слово БАНДЕРОЛЬ. Розглянемо шифрувальну таблицю з ключем, поданим у табл. 5.9
Таблиця 5.9 - Шифрувальна таблиця з ключевим словом
| Б | А | Н | Д | Е | Р | О | Л |
| Ь | В | Г | Є | Ж | З | И | І |
| Ї | Й | К | М | П | С | Т | У |
| Ф | Х | Ц | Ч | Ш | Щ | Ю | Я |
Як і в разі полібіанського квадрата, при шифруванні відшукують у цій таблиці чергову літеру відкритого тексту і записують у шифртекст літеру, розташовану нижче за неї в тім самім стовпці. Якщо літера тексту міститься в нижньому рядку таблиці, тоді для шифртексту беруть першу верхню літеру з того ж самого стовпця.
Наприклад, при шифруванні за допомогою цієї таблиці повідомлення
ДІЛОМАЙСТРАВЕЛИЧАЄ
дістаємо шифртекст
ЄУІИЧВХЩЮЗВЙЖІТДВМ
Такі табличні шифри називаються монограмними, тому що шифрування виконується за однією літерою.
5.2.9 Шифрування за допомогою біграмного шифру Плейфейра
Основою шифру Плейфейра є шифрувальна таблиця з випадково розташованими літерами абетки вихідних повідомлень.
У цілому структура таблиці системи шифрування Плейфейра є цілком аналогічна до структури таблиці Трисемуса. Тому для пояснення процедур зашифровування й розшифровування в системі Плейфейра скористаємося таблицею 5.9.
Процедура зашифровування включає такі вимоги:
Відкритий текст вихідного повідомлення розбивається на пари літер (біграми). Текст повинен мати парну кількість літер і в ньому не повинно бути біграм, котрі містили б дві однакові літери. Якщо цих вимог не додержано, то текст змодифіковується навіть через незначні орфографічні помилки.
Послідовність біграм відкритого тексту перетворюється за допомогою шифрувальної таблиці на послідовність біграм шифртексту за такими правилами:
· якщо дві літери відкритого тексту не потрапляють в один рядок чи стовпець (як, наприклад, літери А та И у табл. 5.9), тоді відшукують літери в кутах прямокутника, визначуваного даною парою літер. (У нашому прикладі це літери АИОВ. Пара літер АИ відбивається в пару ОВ.) Послідовність літер у біграмі шифртексту має бути дзеркально розташована стосовно послідовності літер у біграмі відкритого тексту;
· якщо обидві літери біграми відкритого тексту належать до одного стовпця таблиці, то за літери шифртексту вважаються літери, котрі розміщено під ними (наприклад, біграма НК дає біграму шифртексту ГЦ). Якщо при цьому літера відкритого тексту перебуває в нижньому рядку, то для шифртексту береться відповідна літера з верхнього рядка того самого стовпця (наприклад, біграма ВХ дає біграму шифртексту ЙА);
Якщо обидві літери біграми відкритого тексту належать до одного рядка таблиці, то за літери шифртексту вважаються літери, котрі розміщено праворуч від них (наприклад, біграма НО дає біграму шифртексту ДЛ). Якщо при цьому літера відкритого тексту перебуває в крайньому правому стовпці, то для шифру беруть відповідну літеру з лівого стовпця в тому самому рядку (наприклад, біграма ХЯ дає біграму шифртексту ЦФ).
Зашифруємо текст:
ВСЯКИЙ СВОГО ЩАСТЯ КОВАЛЬ
Розбиття цього тексту на біграми дає
ВС ЯК ИЙ СВ ОГ ОЩ АС ТЯ КО ВА Л Ь
Дана послідовність біграм відкритого тексту перетворюється за допомогою шифрувальної таблиці (табл. 5.9) на таку послідовність біграм шифртексту:
ЗЙ ЦУ ВТ ЙЗ НИ РЮ РЙ УЮ ТН ЙВ БІ
При розшифровуванні застосовується зворотний порядок дій.
5.3 Приклади розв’язування криптографічних завдань за
допомогою шифрів складної заміни
5.3.1 Шифрування за допомогою таблиці Віженера
Нехай за ключове обране слово АМБРОЗІЯ. Необхідно зашифрувати повідомлення ПРИЛІТАЮ СЬОМОГО.
Випишемо відкрите повідомлення в рядок і запишемо під ним ключове слово з повторенням. В третій рядок будемо виписувати літери шифртексту, визначувані з таблиці Віженера (Додаток А).
| Повідомлення | П | Р | И | Л | І | Т | А | Ю | С | Ь | О | М | О | Г | О |
| Ключ | А | М | Б | Р | О | З | І | Я | А | М | Б | Р | О | З | І |
| Шифртекст | П | В | І | Б | Ш | Ь | І | Ь | С | Й | П | В | В | Ї | Ш |
5.3.2 Шифрування за допомогою шифру Гронсфельда
Шифр складної заміни, називаний шифром Гронсфельда, являє собою модифікування шифру Цезаря з числовим ключем. Для цього під літерами відкритого повідомлення записують цифри числового ключа. Якщо ключ є коротший за повідомлення, то його запис циклічно повторюють. Шифртекст здобувають приблизно так само, як в шифрі Цезаря, але відлічують за абеткою не третю літеру (як це чинять в шифрі Цезаря), а обирають ту літеру, котру зміщено за абеткою на відповідну цифру ключа. Шифр Гронсфельда являє собою, власне кажучи, окремий випадок системи шифрування Віженера (ключ надається в числовому вигляді), тому для шифрування відкритого повідомлення користуються таблицею Віженера (Додаток А)
Приміром, застосовуючи як ключ групу з чотирьох початкових цифр числа e (основу натурального логарифму), а саме 2718, здобуваємо для відкритого повідомлення БЕЗ ОХОТИ НЕМА РОБОТИ такий шифртекст:
| Повідом-лення | Б | Е | З | О | Х | О | Т | И | Н | Е | М | А | Р | О | Б | О | Т | И | |
| Ключ | |||||||||||||||||||
| Шифр-текст | Г | Й | И | Ц | Ч | Х | У | О | П | Й | Н | З | Т | Х | В | Ц | Ф | Н |
Слід зазначити, що шифр Гронсфельда розкривається відносно легко, якщо врахувати, що в числовому ключі кожна цифра має лише десять значень, а отже, є лише десять варіантів прочитання кожної літери шифртексту. З іншого боку, шифр Гронсфельда припускає подальші модифікування, що вони поліпшують його стійкість, зокрема подвійне шифрування різними числовими ключами.
5.3.3 Шифрування за допомогою подвійного квадрата
1854 року англієць Чарльз Уїтстон розробив новий метод шифрування біграмами, котрий називають подвійним квадратом. Своєї назви цей шифр дістав за аналогією з полібіанським квадратом. Шифр Уїтстона відкрив новий етап в історії розвинення криптографії. На відміну від полібіанського, шифр "подвійний квадрат" використовує одразу дві таблиці (рис.5.7), розміщувані на одній горизонталі, а шифрування здійснюється біграмами, як у шифрі Плейфейра. Ці не надто складні модифікації призвели до з׳являння на світ якісно нової криптографічної системи ручного шифрування. Шифр "подвійний квадрат" виявився вельми надійним та зручним і застосовувався в Німеччині навіть у роки другої світової війни.
Пояснімо процедуру шифрування цим шифром на прикладі. Нехай є дві таблиці з довільно розташованими в них українськими абетками. Перед зашифровуванням повідомлення розбивають на біграми. Кожна біграма шифрується окремо. Першу літеру біграми відшукують у лівій таблиці, а другу літеру – у правій таблиці. Потім подумки будують прямокутник у такий спосіб, аби літери біграми містилися в його протилежних вершинах. Інші дві вершини цього прямокутника надають літери біграми шифртексту.
| Ж | Щ | Н | Ю | Р | И | Ч | Г | Я | Т | ||
| И | Т | Ь | Ц | Б | Ф | Ж | Ь | М | О | ||
| Я | М | Е | Л | С | З | Ю | Р | В | Щ | ||
| В | І | П | Ч | А | Ц | У | П | Е | Л | ||
| Х | Д | У | О | К | Є | А | Н | Б | Х | ||
| З | Є | Ф | Г | Ш | І | К | С | Ш | Д |
Рисунок 5.7 – Дві таблиці з довільно розташованими символами української абетки для шифру "подвійний квадрат"
Припустімо, що шифрується біграма вихідного тексту ИЛ. Літера И міститься в стовпці 1 і рядку 2 лівої таблиці. Літера Л міститься в стовпці 5 і рядку 4 правої таблиці. Це означає, що прямокутник утворено рядками 2 й 4, а також стовпцями 1 лівої таблиці й 5 правої таблиці. Отже, до біграми шифртексту входять літера О, розміщена в стовпці 5 і рядку 2 правої таблиці, і літера В, розташована в стовпці 1 і рядку 4 лівої таблиці, тобто здобуваємо біграму шифртексту ОВ.
Якщо обидві літери біграми повідомлення містяться в одному рядку, то й літери шифртексту беруть з того самого рядка. Першу літеру біграми шифртексту беруть з лівої таблиці в стовпці, який відповідає другій літері біграми повідомлення. Друга ж літера біграми шифртексту береться з правої таблиці в стовпці, який відповідає першій літері біграми повідомлення. Тому біграма повідомлення ТО перетворюється на біграму шифртексту БЖ. В аналогічний спосіб шифруються всі біграми повідомлення:
| Повідомлення | ПО | ВТ | ОР | НА | ПЕ | РЕ | ДА | ЧА | ||||||||
| Шифртекст | ЛЬ | ЛЖ | НЛ | ЧУ | ЧП | ЯА | ДА | УО |
Шифрування методом подвійного квадрата надає вельми стійкий до розкриття і простий у застосуванні шифр. Зламування шифртексту "подвійний квадрат" потребує потужних зусиль, при цьому довжина повідомлення має бути не менш ніж тридцять рядків.
Окремим випадком системи шифрування Віженера є система шифрування Вернама. Конкретна версія цього шифру, запропонована 1926 року Гілбертом Вернамом, співробітником фірми AT&T США, використовує двійкове подання символів вихідного тексту (модуль m = 2).
Кожен символ вихідного відкритого тексту з англійської абетки {А, В, С, D,..., Z}, розширеного шістьма допоміжними символами (прогалина, повернення каретки й т. п.), передусім кодувався в п’ятибітовий блок (b 0, b 1, …, b 4) телеграфного коду Бодо. Випадкова послідовність двійкових ключів k 0, k 1, k 2,... заздалегідь записувалася на паперовій стрічці. Шифрування вихідного тексту, попередньо перетвореного на послідовність двійкових символів х, здійснювалося шляхом додавання за модулем 2 символів х з послідовністю двійкових ключів k. Символи шифртексту
y = x  k.
k.
Розшифровування полягає в додаванні за модулем 2 символів у шифр-тексту з тією самою послідовністю ключів k:
x= y  k = x
k = x  k
k  k.
k.
При цьому послідовності ключів, використовувані при шифруванні й розшифровуванні, компенсують одна одну (при додаванні за модулем 2) – і як наслідок відновлюються символи х вхідного тексту.
При розроблянні своєї системи Вернам перевіряв її за допомогою закільцьованих стрічок, установлених на передавачі й приймачі для того, аби використовувалась одна й та сама послідовність ключів.
Слід зазначити, що метод Вернама не залежить від довжини послідовності ключів і, окрім того дозволяє використовувати випадкову послідовність ключів. Однак при реалізації методу Вернама виникають серйозні проблеми, пов'язані з необхідністю доставляння одержувачеві такої самої послідовності ключів, як і у відправника, або з необхідністю безпечного зберігання ідентичних послідовностей ключів у відправника й одержувача. Ці недоліки системи шифрування Вернама подолано при шифруванні методом гаммування.
Під гаммуванням розуміють процес накладання за певним законом гамми шифру на відкриті дані. Гамма шифру – це псевдовипадкова послідовність, створена за заданим алгоритмом для зашифровування відкритих даних і розшифровування зашифрованих даних.
Практичні роботи
6.1 Практична робота № 1
Модулярна арифметика
Метою роботи є вивчення основних принципів арифметики за модулем. Для цього студент повинен:
· ознайомитися з теоретичними відомостями;
· вміти дати відповіді на контрольні питання;
· вирішити завдання 6.1.1 – 6.1.3
Теоретичні відомості
Розглянемо випадок використання модулярної арифметики у нашому житті. Наприклад, якщо на циферблаті годинника ми бачимо 5 годин, це означає, що зараз може бути чи 5 годин ранку, чи 17 годин вечора. Це арифметика за модулем 12.
Запис в модулярній арифметиці
a ≡ b (mod n)
читається так: число a збігається (конгруентно, тотожно дорівнює, еквівалентно) з числом b за модулем n, якщо є таке число k, що
a ≡ b + k n.
Якщо a ≡ b (mod n), то число b називають лишком числа a за модулем n..
У нашому прикладі 17mod12 = 5 чи 17≡ 5 (mod12) число 5 є лишком числа 17 за модулем 12.
Модулярна арифметика аналогічна звичайній арифметиці. Фактично можна чи по-перше привести до модулю n, а потім виконувати операції, чи по-перше виконувати операції, а вже потім приводити до модулю n.
Так для чисел a ≡ b (mod n) та c ≡ d (mod n) є правила складання та множення:
(a ±c) ≡ (b ± d) mod n, ac ≡ bd mod n
чи
(a ±c) mod n ≡ (a mod n ± c mod n) mod n,
(ac) mod n ≡ [(a mod n)(c mod n)] mod n.
(a (b + c) mod n ≡{[a b(mod n)] +[a c (mod n)]} mod n.
Приклад. (15 + 20) mod 4 ≡ 15 mod 4 +20 mod 4 ≡(3+0) mod 4≡3 mod 4.
Якщо a ≡ b (mod n), то at ≡ bt mod n, де t – ціле число. Ділення має сенс тоді, тобто  mod n, коли
mod n, коли  – ціле число.
– ціле число.
Приклад. Для числа 18 ≡ 4 mod 14 справедливо множення на t =2, тобто 36 ≡ 8 mod 14, але несправедливо ділення на t = 2, тому, що 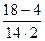 = 0,5 - не ціле число.
= 0,5 - не ціле число.
З правила множення випливає правило піднесення до степеня:
якщо a ≡ b (mod n), то
a m ≡ b m mod n ≡(b mod n) m mod n.
Приклад. 530 mod 3 ≡ (52 mod 3)15 mod 3 ≡ (1 mod 3)15 mod 3≡ 1 mod 3.
Криптографія використовує обчислювання за модулем, тому що задачі типу обчислення дискретних логарифмів та квадратних коренів дуже складні. Крім того, з обчислюваннями за модулем легше працювати, тому що вони обмежують діапазон усіх проміжних величин та результату.
Для модулю n довжиною k біт проміжні результати будь-якого складання, віднімання чи множення будуть не довше за 2k біт. Тому піднесення до степеня в медулярній арифметиці можна виконати без генерації дуже великих проміжних результатів.
Піднесення до степеня числа а за модулем n
ах mod n
можна виконувати, як ряд множення та ділення.
Наприклад, якщо треба обчислити а8 mod n, варто виконати три множення та три приведення до модулю:
((а2 mod n) 2 mod n) 2 mod n..
Якщо треба обчислити двійкове число, тоді число х записують як суму степенів 2:
х = 25 (10)→ 1 1 0 0 1 (2), тому 25 = 24 + 23 + 20.
Тоді
а 25 mod n = (а · а24) mod n = (а ·а 8·а 16) mod n == [ а ·((а 2) 2)2 ·(((а 2)2)2)2] mod n...
Цей метод зменшує трудомісткість обчислень до 1,5х k операцій, де k – довжина числа в бітах.
Так як алгоритми шифрування основані на піднесенні до степеня по модулю, тому доцільно використовувати алгоритми швидкого піднесення до степеня.
Алгоритм Евкліда
За допомогою алгоритму Евкліда можна знайти найбільший спільний дільник (НСД) чисел а та b, тобто НСД (а, b) чи просто (а, b) – це найбільше ціле число, яке одночасно ділить числа а та b без залишку.
Наприклад, (18,9) = 9; (7,3) = 1. Якщо НСД (а, b) = 1, то цілі числа а та b – взаємно прості.
Для опису алгоритму Евкліда припустимо, що а>0, b>0, а>b.
а ≡ с mod b, с>0;
b ≡ d mod с, d>0;
c ≡ e mod d, e>0;
...........................
m ≡ 0 mod n, n>0.
Знайшли НСД (а, b) = n..
Приклад. Знайти НСД (21, 15).
Згідно алгоритму Евкліда можна записати
21 ≡ 6 mod 15, 21 = 1·15 + 6;
15 ≡ 3 mod 6, 15 = 2·6 + 3;
6 ≡ 0 mod 3 6 =2·3 +0.
Так, знайшли НСД (21, 15) = 3.
Кожне ціле число n>1 може бути представлено єдиним чином як добуток простих
З точки зору криптографії позитивним фактом є те, що не відомо ніякого ефективного алгоритму розкладення чисел на множники. Більш того, не відомо ефективнів методів навіть в такому простому випадку, коли необхідно відновити два простих числа p та q з їхнього добутку:
n = p· q
Обчислення обернених величин
У модулярній арифметиці числа а та х є оберненими за модулем n, якщо
ах (mod n) ≡ 1 mod n.
чи
а - 1≡ х mod n,
де а та n - взаємно прості числа.






