   |
- Перемішування – це здатність шифру приховувати статистичну залежність між символами відкритого тексту та символами у відповідній до нього криптограмі. Якщо алгоритм зашифрування забезпечує досить якісне перемішування символів відкритого тексту, то між символами відкритого та закритого текстів не існує ніяких статистичних і функціональних залежностей.
Шифр, що у достатній мірі відповідає цим умовам, може бути розкритий лише повним перебором ключів по всій їх множині. Першою серйозною спробою побудувати такий шифр була система “Люцифер”. Вона передбачає поступове чергування замін та перестановок символів відкритого тексту.
Спрощена система системи “Люцифер” наведена на рисунку 2.7. Перед тим як виконувати зашифрування, повідомлення розподіляють на блоки фіксованої довжини.
У зв’язку із тим, що реалізація замін та перестановок символів вимагає достатньо великої пам’яті, черговий блок інформації, якій підлягає зашифруванню розподіляється на блоки меншої довжини. У наведеному на рисунку прикладі, 16 розрядний блок розділяється на чотири 4-х розрядні блоки, для кожного з яких передбачається наявність 32-х бітного блоку пам’яті S, що забезпечують заміну вхідних символів. Якщо обмежитись одним блоком пам’яті на всі 16 розрядів, то його загальний об’єм складав би 216 бітів або 16384 байтів, тобто у 1024 разів більше.
Виходи всіх блоків S під’єднуються до загального блоку Р, що забезпечує перестановку вхідних символів. Загальна пам’ять, що потребує реалізація такого блоку має складати лише 32 біти. Саме виконання рівномірної перестановки у межах всього 16-ти розрядного блоку надає ефективність розсіюванню символів блоку, що підлягає зашифруванню.
Для того щоб наведена система забезпечувала високу криптографічну стійкість, кількість етапів чергування замін та перестановок повинна бути великою, а кожен символ на її виході повинен бути складною функцією від символів на всіх її входах. Що стосується секретності цієї системи, то для її забезпечення необхідно, щоб заміни та перестановки, які виконуються блоками S та Р відповідно, були параметричними. Це означає, що для кожного етапу криптографічного перетворення має існувати свій окремий і незалежний від інших ключ Кі.
Система “Люцифер” була майже єдиною спробою реалізувати ефективну лінійну систему криптографічного перетворення, що виконувались корпорацією ІВМ. Як спало ясно пізніше, забезпечення необхідної криптографічної стійкості у такій системі вимагало великої кількості етапів шифрування і, як слідство, великих обчислювальних ресурсів.
Другий спосіб формування складних криптографічних систем називається “ виваженою сумою ” і передбачає наявність декількох простих систем (двох і більше, наприклад R1 і R2). Кожного разу, перед зашифруванням чергового повідомлення, випадковим чином з імовірністю р, обирається система шифрування R1, або система шифрування R2, з імовірністю q = 1- р. Таким чином, в загальному випадку, у криптографічному перетворені повідомлення буде брати участь одна із двох окремих секретних систем із загальною областю визначення за правилом 
. Щоб таку систему можна було практично реалізувати, необхідно, щоб вибір секретної системи повністю визначався складом ключа. В цьому разі буде забезпечено співпадання процедур зашифрування та розшифрування як на стороні джерела повідомлень, так і на приймальній стороні.
Наведена система передбачає наявність т ключів, що обираються відповідно з імовірностями
кожен з яких перетворює повідомлення Ті в одну з т можливих криптограм. Якщо на основі обраного ключа буде вибрана система R1, то повідомлення Ті буде перетворене на одну з криптограм 
з імовірностями 
Якщо ж, навпаки, буде обрано систему R2, це повідомлення буде перетворене на одну з криптограм 
з імовірностями 
Наведений спосіб формування композиційного шифру дає змогу робити вибір з будь-якої кількості секретних систем. У загальному випадку її можна представити як
Це означає, що криптоаналітик супротивника крім визначення ключа, має робити вибір щодо секретної системи, що значно ускладнює задачу дешифрування. Щоб це було насправді так, алгоритм вибору системи повинен також триматись в секреті.
2.4 Загальні відомості про блочні шифри.
При блочному шифруванні вихідний текст спочатку розбивається на однакові по довжині блоки, а потім для перетворення блока відкритого тексту в блок шифртексту застосовується функція шифрування, яка залежить від ключа.
Розподілення повідомлення на блоки пов’язане із технічними та алгоритмічними особливостями реалізації криптографічних систем.
Вибір довжини блоку визначає потужність вхідного алфавіту. Збільшення такої потужності викликає необхідність попереднього дослідження обраних способів криптографічних перетворень, які обираються до складу алгоритму шифрування. При цьому критерієм якості способу розподілення на блоки та архітектури створеного алгоритму обираються експлуатаційні характеристики криптографічної системи. У принципі, потужність вхідного алфавіту, в першу чергу залежить від довжини слова мікропроцесору, що використовується обчислювальною системою, яка є у розпорядженні власників інформаційних ресурсів і потенційних порушників.
Блочні шифри, на відміну від поточних, мають додаткові можливості підвищення їх криптографічної стійкості.
Під час шифрування текстів з малою ентропією мається можливість побудови для них статистичних способів дешифрування, подібних до тих, що використовуються під час аналізу шифрів простої заміни. Підвищення довжини вхідного слова викликає зростання “середньої ентропії на знак”, а це, у свою чергу, приводить до нелінійного зростання складності статистичного криптоаналізу зашифрованого тексту.
Зворотною стороною зростання складності криптоаналізу блочних шифрів є складність доказового обґрунтування їх криптографічної стійкості.
Щоб обійти цю проблему, довжина блоку обирається не дуже великою і операції шифрування, що входять до складу алгоритму шифрування повторюються кілька разів. У більшості криптографічних систем, які були запропоновані розробниками у якості державних стандартів протягом 70 – 80 років двадцятого сторіччя, довжина блоку дорівнює 64-м бітам. Якщо довжину блоку зробити меншої довжини, дешифрування криптограм легко виконується із застосуванням невеликих обчислювальних ресурсів. На відміну, збільшення цієї довжини приводить до зростання терміну шифрування та кількості необхідних обчислювальних ресурсів.
Усі блочні шифри мають ще два суттєвих недоліки, для усунення яких необхідно приймати спеціальні міри.
Перший полягає у тому, що довжина вхідного слова, передбаченого алгоритмом шифрування є фіксованою, а повідомлення, які підлягають шифруванню, в загальному випадку мають довжину, що не є кратною довжині вхідного слова. Це означає, що останній блок, як правило, буде мати меншу довжину. Якщо доповнити його будь-якими символами, наприклад нулями, то, у середньому, половина останнього блоку буде відома криптоаналітикові супротивника. А це, у свою чергу, значно зменшить криптографічну стійкість алгоритму шифрування. З ціллю подолання такого недоліку, розроблені як загальні, прийнятні для усіх блочних алгоритмів способи, так й індивідуальні, прийнятні для конкретних криптографічних систем.
Друга проблема полягає у тому, що однакові блоки будуть зашифровані однаково, а це дозволить супротивникові отримувати допоміжну інформацію, що значно підвищить його можливості у виконанні статистичного криптоаналізу. Для усунення цього недоліку також, у свій час, було запропоновано відповідні міри захисту, опис яких буде наведено далі.
В сучасних блочних шифрах блоки відкритого тексту і шифртексту уявляють собою двійкові послідовності довжиною звичайно 64 біта. Тобто кожний блок може приймати 264 значень. Тому підстановки виконуються в абетках дуже великого розміру (264 ≈ 1019 „символов”)
Під N – розрядним блоком будемо розуміти послідовність з одиниць і нулів довжини N3:
х = (х 0, х 1, …, хn -1)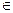 
Z2,N;
х в Z2,N можна тлумачити як вектор та як двійкове уявлення цілого числа
= 
.
Наприклад, якщо N = 4, то
(0,0,0,0) → 0 (0,1,0,0) → 4 (1,0,0,0) → 8 (1,1,0,0) → 12
(0,0,0,1) → 1 (0,1,0,1) → 5 (1,0,0,1) → 9 (1,1,0,1) → 13
(0,0,1,0) → 2 (0,1,1,0) → 6 (1,0,1,0) → 10 (1,1,1,0) → 14
(0,0,1,1) → 3 (0,1,1,1) → 7 (1,0,1,1) → 11 (1,1,1,1) → 15
Незважаючи на те, що блочні шифри є випадковою подією підстановок (тільки на абетках дуже великого розміру), їх треба розглядати окремо.
По-перше, більшість симетричних шифрів, які використовуються в системах передавання повідомлень, є блочними шифрами.
По-друге, блочні шифри зручніше описувати в алгоритмічному вигляді, а не як звичайні підстановки.
Блочним шифром будемо звати елемент p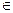 
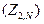, p: х→ у = p (x), де х = (х 0, х 1, …, хN -1), (у 0, у 1, …, уN -1)
Припустимо, що
p (xi) = уi, 0 ≤ i < m,
для деякого p 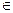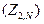, вихідного тексту Х = { xi: xi 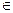Z2,N } та шифртексту Y = { уi }.
Якщо х 
{ xi },то p (xi) { уi }, так як p є перестановкою на Z2,N.
Коли відомо, що p належить невеликій підмножині П з 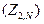, тоді можна зробити деякий висновок. Наприклад, коли
П = { pj: 0 ≤ j< 2N }, pj(i) =(i+j) (mod2N), 0 ≤ i < 2,
то значення p (x)при завданном значенні х однозначно визначає p. В цьому випадку Х є підмножиною підстановки Цезаря на Z2,N.
Криптографічне значення цієї властивості повинне бути явним: якщо вихідний текст шіфрується підстановкою p, яка вибрана з повної симетричеської групи, тоді злочинець, що буде шукати відповідність вихідного та шифрованного текстів
xi ↔ уi, 0 ≤ i < m,
не зможе визначити вихідний текст, який відповідав би у { уi }.
Якщо для шифрування вихідного тексту використовується підсистема
p з П 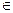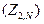,тоді систему, яка буде одержана після підстановок П будемо називати системою блочних шифрів чи системою блочних підстановок.
Ключевою системою блочних шифрів є підмножина П[К] симетричеської групи
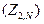
П[К] = { p {k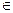}:k K},
яке індексується по параметру k 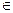K; де k – ключ, а К – простір ключей. При цьому треба, щоб різні ключи відповідали різним підстановкам Z2,N.
Ключева система блочних шифрів П[К] використовується наступним образом. Користувач i такористувач j деяким образомукладають згоду відносно ключа k зК, вибираючи, таким чином, елемент з П[К] та передають текст, який зашифровуваний з використанням обранної підстановки. Для того, щоб обозначити N – розрядний блок шифрованного тексту, який відповідає N – розрядному блоку вихідного тексту х з використанням підстановки p {k} за допомогою ключа k наведемо запис
y = p {k,х}.
Припустімо, що злочинцю
· Відомий простір ключей;
· Відомий алгоритм визначення підстановки p {k} по значенню ключа k;
· Невідомо, який саме ключ обрано користувачем.
Тоді злочинець може:
· Получити ключ внаслідок недбалості користувача i такористувача j;
· Перехопити (шляхом перехоплення телефонних та комп’ютерних повідомлень) шифрованний текст y, який передається від користувача i докористувача j, а потім „перебирати” усі ключи з ключевого простіру К доки не буде одержане повідомлення вихідного тексту, яке можна було б розуміти.
· Получити відповідні вихідний та шифрованний тексти (x ↔ у) та скористатися методом „перебирання” усіх ключів з ключевого простіру К.
· Зробити каталог N – розрядних блоків, де записувалась частість їх появи в вихідному та шифрованному текстах. Каталог дає змогу вишуковувати найвірогідніші слова, користуючись при цьому наступною інформацією:
- листинг на мові асемблеру характеризується дуже виявленним структурованним форматом;
- цифрове уявлення графічної та звукової інформації має невеликий набір знаків.
Припустімо, що N = 64та кожний елемент 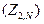може використовуватися як підстановка, так що К =
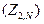
Тоді
· Існує 264 64-розрядних блоків; злочинець не може використовувати каталог з 264≈1.8·1019 рядками;
· Випробування на ключ при кількості ключів, які дорівнюють (264)!, практично є неможливими; відповідність вихідного та зашифровуванного текстів для деякіх N – розрядних блоків p {k,xi} = уi, 0 ≤ i < m, не дає злочинцю ніякої інформації відносно значення p {k,x} для x { x i }.
Системи шіфрування з блочними шифрами, абеткою Z2,64 та простіром ключів
К = 
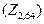є неподільними (тому, що виходить за межі можливості як, злочинця, так і того користувача, що створив вихідний текст).
Таким чином, вимоги до блочного шифру визначаються у наступному. Необхідно:
· Досить велике N ( 64 чи більше) для того, щоб ускладнити користування каталогом;
· Досить великий простір ключів для того, щоб виключити змогу підбору кдючів;
· Складні співвідношення p {k,x}: х→ у = p (k,x) поміж вихідним повідомленням та шифртекстом для того, щоб аналітичні та/чи статистичні методи визначення вихідного тексту та/чи ключа на базі відповідності вихідного повідомлення та шифртексту було не можна реалізувати.
2.5 Генерування блочних шифрів.
2.5.1 Використання нелінійних структур для побудови блочних шифрів.
Комбінація простих шифруючих перетворень у лінійний ланцюжок дозволяє створити цілком надійний складний шифр. Проблема полягає в тому, що для рішення цієї задачі потрібна занадто велика кількість перетворень.
З цієї причини в сучасних криптосистемах поширилась інша схема, відмінність якої складається у використанні нелінійних структур і операцій над шифруючими блоками даних.
Нелінійність структури шифруючого перетворення набагато ускладнює процедури криптоаналізу.
Застосування, на додаток до цього, в алгоритмі шифрування операцій функціонального перетворення, також істотно ускладнює процедуру перетворення шифруючого блоку (числа можливих варіантів).
Встановлено, що більш вигідно не перетворювати переданий блок відповідно до застосовуючого ключа, а спочатку скомбінувати цей блок зі значенням ключа, а вже потім, піддавати його деякому перетворенню.
Ті
Кі Варіант попередньої комбінації даних і ключа |
У сучасних криптографічних системах, застосовують, як правило, аддитивні і, значно рідше, мультиплікативні операції над шифруючими даними.
Варто мати на увазі, що, застосовуючи деяку операцію «°», необхідно
 Ti
Ki
Ti+1
|
подбати, щоб для неї існувала зворотна їй операція«·». Тобто вона повинна бути придатна для реалізації умов побудови симетричної криптосистеми.
(Т ° К) · К = Т
| Ti Ki Ti+1 |
Складність операції також може бути підвищена, якщо комбінувати з даними не сам ключ, а деякий скомбінований з нього код, що залежить від даних.
Тi+1 = Тi ° f (Тi, Кi).
У загальному виді, цю функцію можна записати так
Тi+1 = F(Тi, Кi).
Відмінність цих виразіву тому, що функція F повинна мати зворотну операцію, а функція f – не обов'язково.
Від функції f потрібна максимально можлива складність (число можливих варіантів перетворення) і нелінійність перетворень. Іншою вимогою до функції є виконання умови зворотності перетворень.
Складність проблеми в тім, що зворотність перетворень є особливістю лінійних систем. Рішення нелінійних рівнянь щодо одного з аргументів у загальному виді відсутнє.
Зворотність виразу означає, що повинна існувати ефективно обчислююча функція g (Тi+1, Кi) задовольняюча умові
F(Тi Кi) = g (Тi+1, Кi).
Зі сказаного випливає, що для побудови ефективного шифру варто визначити пари функцій, що були б нелінійні і, у той же час, зворотні одна одній.
Прикладом пари операцій такого типу, які широко застосовуються у сучасних симетричних криптосистемах, служать наступні перетворення.
2.5.2Використання мереж Фейстеля.
Самим розповсюдженим способом створення блочних шифрів є використання мереж Фейстеля (Рис.2.9).
Підвищення ефективності шифрування було можливим лише у разі відмови від лінійної структури алгоритму. Але, в цьому разі, дуже важко забезпечити зворотний характер криптографічних перетворень. Проблема була у тому, щоб побудувати алгоритм, який не містив би їх взагалі. І ця задача була вирішена співробітниками лабораторії фірми IBM Watson Research Lab нової оригінальної архітектури симетричного шифру на базі незворотних перетворень.
Як відомо, ідея використання зворотної операції ”додавання по модулю два”, виникла досить давно. Її запропонував ще Вернам у 1925 році для побудови шифру, що, як стало зрозуміло значно пізніше, був досконалим. Стійкість такого способу визначається властивостями шифрувальної гамми. Спосіб її формування є найскладнішою з проблем сучасної криптографії.
 |
Рисунок 2.9 Схема мережі Фейстеля
Якщо гамма побудована за допомогою будь-якого, реалізованого програмним методом генератору, вона обов’язково буде рекурентною, тобто, її зміст буде мати кінцеву довжину і буде циклічно повторюватись через певну кількість кроків. Визначивши період повторення такої гамми, знайти її зміст не так складно. В усякому разі, ця задача не є складною для криптоаналітика, що має
 |
досить великі обчислювальні ресурси. Якщо ж формувати гамму за допомогою складних апаратних засобів, які використовують не рекурентні, а реальні випадкові процеси, процедура розподілу ключової інформації стає занадто складною.
Хорст Фейстель підійшов до проблеми наступним чином. Він запропонував формувати шифрувальну гамму з самої інформації, яка підлягає шифруванню.
Спочатку масив інформації, який має бути зашифрованим розділяється на блоки фіксованої довжини. Кожен з таких блоків під час кожної ітерації шифрування розділяється на дві однакові частини: ліву Li і праву Ri . Потім з правої частини формується шифрувальна гамма, довжина якої дорівнює половині блоку. Принцип її формування визначається за допомогою складного нелінійного функціонального перетворення Fi (Ri, Кі), що залежить від ключа. Перша (ліва) половина нового (утвореного протягом однієї ітерації) блоку Li+1 утворюється з правої половини попереднього блоку Ri , тобто
Щодо другої (правої) половини нового блоку, то вона є результатом гаммування лівої половини попереднього блоку (складанням її ”по модулю два” зі створеною гаммою) за правилом
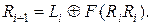
Як видно із цього виразу, перетворення правої частини блоку залежить від змісту ключа Кі. Це означає, що для кожної ітерації шифрування потрібен окремий ключ. Таким чином, як і у схемі, яку запропонував К. Шеннон, кожне перетворення блоку, який підлягає шифруванню має бути параметричним (тобто таким, що залежить від деякого параметру). Крім того, зважаючи на те, що протягом однієї ітерації буде зашифрованою лише половина блоку, загальне їх число має бути парним. І самі ключі Кі , і функції Fi (Ri, Кі), можуть мати свій власний вигляд для кожного етапу шифрування. Що стосується проміжних ключів, то вони можуть бути сформовані з головного ключа за допомогою якого-небудь алгоритму або окремо, таким чином, щоб вони були незалежні один від одного.
У разі якщо довжина лівої частини блоку дорівнює довжині його правої частини, має місце так звана збалансована схема Фейстеля. В другому разі – це розбалансована схема Фейстеля. Це, у свою чергу, вимагає формування різних по довжині шифрувальних гамм, і різних функцій для виконання відповідних нелінійних перетворень, в залежності від номеру ітерації.
Звичайно виникає питання про те, чи буде перетворення, яке виконано за допомогою схеми Фейстеля зворотним? Властивість схеми Фейстеля полягає в тому, що навіть коли у якості нелінійного перетворення використовується функція, яка сама не є зворотною, або до якої не існує зворотної функції, перетворення залишається зворотнім. Справа тут у тому, що для виконання зворотного перетворення не треба обчислювати функцію Fi-1(Ri, Кі). Єдине, про що слід пам’ятати – під час розшифровування даних проміжні ключі мають використовуватися у зворотному порядку. Більш того, схема Фейстеля є симетричною.
 |
Наявність у алгоритмі операції “додавання по модулю два”, дозволяє виконувати операції розшифрування даних за допомогою того самого алгоритму, яким вони були зашифровані.
Стійкість криптосистеми, що побудована на основі схеми Фейстеля, цілком залежить від вигляду нелінійної функції гаммування Fi (Ri, Кі), яке виконується протягом кількох ітерацій. Через це, для забезпечення надійного зашифрування загальне число етапів повинно бути досить великим. Чим більше їх кількість, тим краще виконується розсіювання та перемішування символів відкритого тексту і тим вище стійкість шифру до диференціального та лінійного криптоаналізу.
Практично всі відомі шифри побудовані на основі збалансованої схеми Фейстеля, а нелінійне функціональне перетворення, що використовується на кожному етапі шифрування одне і теж. Такі схеми називають гомогенними, а у протилежному випадку гетерогенними. Використання гетерогенної схеми Фейстеля забезпечує вищу стійкість шифрів, але їх побудова уявляє собою дуже складну задачу, через необхідність забезпечення зворотності алгоритму шифрування. Популярність гомогенної збалансованої схеми визначається тим, що їх реалізація значно дешевше, швидкість шифрування вище, а необхідна стійкість легко досягається ускладненням нелінійної функції шифрування та незначним збільшенням числа етапів перетворення відкритого тексту.
