Вариант – 1.
1. Записать комплексные числа в тригонометрической и в показательной формах:
а) 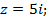
б) 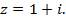
2. Представьте в алгебраической и показательной формах комплексные числа:
а) 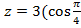 +i
+i 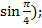
б) 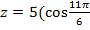 +i
+i 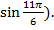
3. Даны комплексные числа 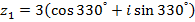 и
и 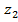
 (
(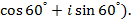
Найти: а) 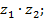 б)
б) 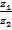 ; в)
; в)  .
.
Вариант – 2.
1. Записать комплексные числа в тригонометрической и в показательной формах:
а) 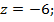
б) 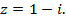
2. Представьте в алгебраической и показательной формах комплексные числа:
а) 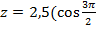 +i
+i 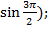
б) 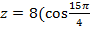 +i
+i 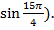
3. Даны комплексные числа 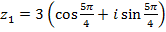 и
и 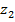
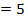 (
(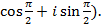
Найти: а) 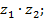 б)
б) 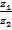 ; в)
; в)  .
.
Вариант – 3.
1. Записать комплексные числа в тригонометрической и в показательной формах:
а) 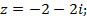
б) 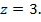
2. Представьте в алгебраической и показательной формах комплексные числа:
а) 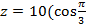 +i
+i 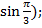
б) 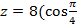 +i
+i 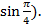
3. Даны комплексные числа 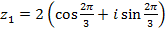 и
и 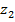
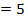 (
(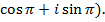
Найти: а) 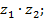 б)
б) 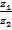 ; в)
; в)  .
.
Вариант – 4.
1. Записать комплексные числа в тригонометрической и в показательной формах:
а) 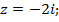
б) 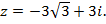
2. Представьте в алгебраической и показательной формах комплексные числа:
а) 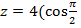 +i
+i 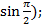
б) 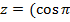 +i
+i 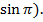
3. Даны комплексные числа 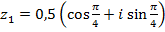 и
и 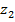
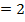 (
(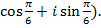
Найти: а) 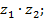 б)
б) 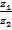 ; в)
; в)  .
.
Контрольные вопросы по теме.
- Как записывается комплексное число в тригонометрической форме?
Как записывается комплексное число в показательной форме? Формула Эйлера.
- Сформулируйте правило перехода от алгебраической формы комплексного числа к тригонометрической и обратно.
- Сформулируйте правило перехода от алгебраической формы комплексного числа к показательной и обратно.
- Как перейти от тригонометрической формы комплексного числа к показательной и обратно.
- Как умножаются комплексные числа, записанные в тригонометрической форме.
- Как умножаются комплексные числа, записанные в показательной форме?
- Сформулируйте правило деления комплексных чисел в тригонометрической форме.
- Сформулируйте правило деления комплексных чисел в показательной форме.
- Как возвести в степень комплексное число, записанное в тригонометрической форме.
- Как возвести в степень комплексное число, записанное в показательной форме?
- Сформулируйте правило извлечения корня n –й степени из комплексного числа, записанного в тригонометрической форме.
- Сформулируйте правило извлечения корня n –й степени из комплексного числа, записанного в показательной форме.
- Сколько значений имеет корень n-й степени из комплексного числа?
Практическое занятие №11
Тема: Действия с матрицами. Вычисление определителей матриц.
Цель: Приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по вычислению определителей 2-го и 3-го порядков, выполнения действий над матрицами, нахождению алгебраических дополнений. Повторить и систематизировать знания по данной теме.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Учебник:
Индивидуальные карточки с вариантом практической работы.




