Формула и схема Бернулли
Пусть многократно реализуются повторные испытания при неизменных условиях их проведения. В ходе испытания фиксируется появление некоторого случайного события А, вероятность появления которого – Р(А) не зависит от результатов предыдущих испытаний и остается неизменной (Р(А)=const) при
повторении опыта. Такие испытания называются независимыми, а схема проведения испытаний носит название схемы Бернулли.
Вероятность 
того, что событие А наступит ровно m раз в n независимых испытаниях, удовлетворяющих условиям схемы Бернулли равна:
,
где:p=P(A)–вероятность наступления события А; и q=1-p.
Пример 1. Вероятность выигрыша по лотерейному билету равна 0,05. Какова вероятность того, что среди купленных 10 билетов окажутся 2 выигрышных.
Решение. Данная задача описывается схемой Бернулли: проводится 10 испытаний, в ходе которых проверяется наличие выигрыша. Применяя формулу Бернулли, находим вероятность появления выигрыша в двух из десяти испытаний:
.
Пример 2. При проведении маркетинговых исследований выявлено, что 20% опрошенных предпочитают использовать продукцию данной фирмы. Найти вероятности возможного числа пользователей продукцией фирмы в произвольно выбранной группе из пяти человек.
Решение. Согласно условию задачи вероятность того, что человек использует продукцию данной фирмы равна 0,2 (т.е: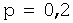 
и 
). Искомые вероятности находим по формуле Бернулли (где: n=5; и m=1,…,5) и помещаем их в таблицу.
| № п.п. | Число пользователей продукцией фирмы в группе из пяти человек | Вероятность рассматриваемого события ( )
|
| Пользователей нет | 
| |
| Один пользователь | 
| |
| Два пользователя | 
| |
| Три пользователя | 
| |
| Четыре пользователя | 
| |
| Все используют продукцию данной фирмы | 
|
Асимптотические приближения формулы Бернулли
Формула Бернулли дает точное значение вероятности того, что событие А наступит ровно m раз в n независимых испытаниях, определяемых схемой Бернулли. Однако, практическое применение этой формулы часто оказывается затруднительным, если числа m и n достаточно велики, а вероятность р – мала. Существуют некоторые асимптотические приближения формулы Бернулли.
Формула Пуассона
Теорема. Если вероятность p наступления некоторого события А в каждом испытании, определяемом схемой Бернулли, стремится к нулю ( 
) при неограниченном увеличении числа испытаний n (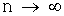 
), а произведение np стремится к некоторой константе 
( 
), то вероятность того, что событие А наступит
ровно m раз в n испытаниях удовлетворяет предельному равенству: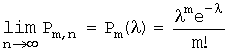 
.
С практической точки зрения, условия и выводы данной теоремы означают, что при выполнении следующих трех условий:
а)вероятность p наступления некоторого события А в каждом испытании, определяемом схемой Бернулли, достаточно мала;
б)число испытаний n – велико;
в)произведение np не превышает десяти (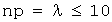 
),
то с достаточно высокой степенью точности формула Бернулли может быть аппроксимирована следующей формулой (Пуассона): 
, где: 
.
