Пусть из 
единственно возможных, несовместных и равновероятных событий 
, 
, …, 
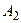событию А благоприятствует m событий, событию В – k событий, событию АВ – r событий (
, 
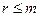). Если событий В произошло, то это означает, что наступило одно из событий 
, благоприятных событию В. При этом условии событию А благоприятствуют r и только r событий , благоприятных АВ. Таким образом 
. (1)
Аналогично, если 
, то 
. (1’)
Если В (соответственно, А) есть невозможное событие, то равенство (1) (соответственно (1’)) теряет смысл.
При 
каждое из равенств (1) и (1’) равносильно так называемой теореме умножения вероятностей.
Теорема умножения вероятностей. Вероятность произведения событий А и В равна произведению вероятности одного из этих событий на условную вероятность другого, при условии, что первое произошло: 
(2).
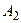Доказательство теоремы умножения вероятностей для классической схемы случаев. Пусть из единственно возможных, несовместных и равновероятных событий , , …, событию А благоприятствует m событий, событию В – k событий, событию АВ – r событий (, 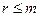). Тогда 
, 
, а 
(из общего решения задачи о нахождении условной вероятности). Подставляя полученные значения вероятностей в формулу (2), получим тождество. Теорема доказана.
Замечание. Теорема умножения справедлива и в том случае, когда одно из событий А или В есть невозможное событие, так как в этом случае вместе с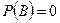 
имеют место равенства 
и 
.
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 3. В ящике находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в ящик. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный и при третьем – синий.
Решение. Пусть событие А – при первом испытании появится белый шар, событие В – при втором испытании появится черный шар; событие С – при третьем испытании появится синий шар. Вероятность появления белого шара при первом испытании 
. Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, то есть условная вероятность 
. Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором черный: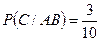 
. Так как события А, В и С совместны, то искомая вероятность
.
Определение 2. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет:
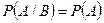(3)
(наступление события В не меняет вероятности события А).
Определение 3. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Замечание 1. Если событие А независимо от события В, то в силу (2) имеет место равенство 
Отсюда следует, что 
, (4)
Т.е. событие В также независимо от А. Таким образом, при сделанном предположении свойство независимости событий взаимно.
Замечание 2. Понятие независимости событий играет значительную роль в теории вероятностей и её приложениях. В практических вопросах для определения независимости событий редко обращаются к выполнению равенств (3) и (4). Обычно для этого пользуются интуитивными соображениями, основанными на опыте (пример с монетой и др.). Для независимых событий теорема умножения вероятностей имеет наиболее простой вид.
Теорема умножения вероятностей для независимых событий. Вероятность произведения двух независимых событий равна произведению их вероятностей:
.
Замечание 3. Если независимость событий определить посредством равенства , то это определение верно всегда, в том числе и тогда, когда и .
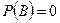Определение 4. События 
, 
, …, 
называются независимыми в совокупности, если для любого события 
из их числа и произвольных 
, 
, …, 
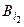взаимно независимы.
Замечание 4. В силу замечания 3 это определение эквивалентно следующему.
Определение 4’. При любых 
и 
.
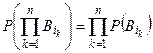Замечание 5. Для независимости в совокупности нескольких событий недостаточно их попарной независимости.
Пример. Грани тетраэдра окрашены: 1-я – в красный цвет, 2-я – в зелёный, 3-я – в синий, 4-я – во все эти 4 цвета (АВС). Легко видеть, что вероятность того, что грань, на которую упадёт тетраэдр при бросании, имеет красный цвет, равна 0,5: граней 4, 2 из них имеют в окраске красный цвет. Тогда 
. Аналогично можно подсчитать, что
.
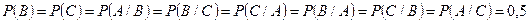Таким образом, события А, В, С попарно независимы. Однако, если осуществились события В и С вместе, то и осуществилось событие А, т.е. 
. Следовательно, события А, В и С в совокупности зависимы.
Обобщение теоремы умножения вероятностей на случай произвольного конечного числа независимых событий: 
.
Пример 4. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна 
. Стрелок произвел три выстрела. Найти вероятность того, что он попал три раза.
Решение. Пусть событие А – стрелок попал в мишень при первом выстреле, событие В – стрелок попал в мишень при втором выстреле; событие С – стрелок попал в мишень при третьем выстреле. Вероятности этих событий по условию равны между собой: 
. Так как вероятность попадания в цель при каждом из выстрелов не зависит от результата остальных выстрелов, то все три события независимы в совокупности, тогда 
.
Следствие. (Теорема о вероятности появления хотя бы одного из совокупности независимых событий). Вероятность появления хотя бы одного из совокупности независимых событий А 1, А 2, …, Аn равна разности между единицей и произведением вероятностей противоположных событий 
, 
, …, 
: 
.
Пример 5. Вероятности попадания в цель при стрельбе из трех орудий соответственно равны: 
; 
; 
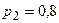. Найти вероятность попадания хотя бы одним из орудий при одном залпе из всех орудий.
Решение. Пусть событие А – попадание в цель хотя бы одним из орудий при одном залпе из всех орудий, событие А 1 – попадание в цель первым орудием, А 2 – попадание в цель вторым орудием, А 3 – попадание в цель третьим орудием. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому события А 1, А 2, А 3 независимы. Вероятности событий, противоположных событиям А 1, А 2, А 3 (то есть вероятности промахов), соответственно равны:
; 
; 
.
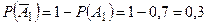Тогда искомая вероятность 
.
Замечание 6. Формула (1’), которая в случае классического определения вероятности выводится из определения условной вероятности, в случае аксиоматического определения вероятности будет взята в качестве определения. Таким образом, в общем случае при по определению полагаем (в случае условная вероятность 
остаётся неопределённой). Это определение позволяет перенести на общее понятие вероятности все определения и результаты настоящего параграфа.
