При проектировании инструментов приходится различать теоретические и технологические параметры установки инструмента относительно детали.

Рисунок 2.7 – Теоретические параметры установки дисковой фрезы относительно сверла: m – межосевое расстояние; ε – угол скрещивания осей винтовой поверхности и инструмента; ψ – угол поворота линии  межосевого расстояния относительно оси x
межосевого расстояния относительно оси x
Теоретические параметры определяют положение системы координат инструмента относительно системы координат детали и необходимы для ведения расчетов. Технологические параметры необходимы для непосредственной установки инструментов относительно детали на станке и определяются в каждом конкретном случае от базовых поверхностей инструмента с учетом конструктивного оформления инструмента и технологических удобств выполнения операции обработки детали. Между теоретическими и технологическими параметрами установки инструмента должны существовать аналитические зависимости, далее они будут рассмотрены. От того, какими будут приняты значения параметров установки фрезы (рисунок 2.7) зависят не только конструктивные, технологические и эксплуатационные показатели инструмента, но и сама возможность обработки винтовой поверхности.
При выборе положения оси фрезы относительно заготовки сверла нужно, с одной стороны, обеспечить возможность получения заданной формы канавки, а с другой - обеспечить наиболее рациональную форму фрезы.
Обычно при практически удобных значениях параметров m, ε и ψ установки оси фрезы невозможно получить канавку сверла без частичного подрезания ее профиля в районе точек С или В, так как подрезание возникает вследствие невыполнения второго или третьего условий формообразования винтовой поверхности (рисунок 2.11). Это нужно иметь в виду и выбирать положение оси фрезы так, чтобы наверняка исключить подрезание участка ВК, образующего главную режущую кромку сверла, а подрезание участка СК свести до минимума.
На участке ВК (рисунок 2.6) профиля канавки наиболее трудной для формообразования является зона, прилегающая к точке В, лежащей на наружном цилиндре. Поэтому, обычно, сначала рассчитывают параметры установки фрезы r в, δв, ξв, ρв для точки В профиля винтовой канавки сверла, чтобы проверить безусловное выполнение всех трех условий формообразования в этой точке.
Теоретический анализ по выполнению требований условий формообразования винтовых канавок сверл дисковыми инструментами [2, 3, 4] показал, что решение этой задачи зависит от соотношения следующих расчетных параметров: углов ε, ψ и межосевого расстояния m (рисунок 2.7); угла наклона винтовой линии ω; диаметров сверла: наружного D и сердцевины do. Оптимальные значения параметров установки фрезы зависят от величины различных параметров сверла, которые на практике изменяются в очень широких границах, и поэтому могут быть уточнены только в каждом конкретном случае обработки винтовой канавки. Наибольшее влияние на выполнение условий формообразования винтовых канавок у сверл оказывают диаметр сердцевины сверла do и угол наклона винтовой канавки ω:
● при увеличении угла ω возможность выполнения третьего условия формообразования в точке В снижается.
● при увеличении отношения do/D, что имеет место для сверл малого диаметра, резко снижается возможность выполнения второго и третьего условий формообразования участка СК профиля канавки, почему на практике очень часто у сверл малого диаметра канавка получается «разваленной».
Для наиболее распространенных диаметров сверл 10−40 мм некоторые установочные параметры фрезы относительно сверла рекомендуется определять следующим образом:
а) при увеличении межосевого расстояния m возможность выполнения всех трех условий формообразования винтовых канавок несколько уменьшается, причем влияние угла ε на условия формообразования возрастает, а угла ψ − убывает;
при m = ∞ параметр ψ на условия формообразования не влияет; Межосевое расстояние m (рисунок 2.7 и 2.8) на начальном этапе определяют по формуле
m ≈ (Df + do) / 2 (2.19)
где Df − предварительный диаметр фрезы (таблица 2.1);
б) при увеличении угла ψ возможность выполнения условий формообразования для точек участка ВК уменьшается, а для точек участка СК − увеличивается. Угол ψ можно принять на начальном этапе в пределах 14º − 27°.
в) при увеличении угла ε возможность выполнения второго условия формообразования для точек участка СК увеличивается, а для точек участка ВК − уменьшается. Значение угла ε при выбранных m и ψ должно быть принято таким, чтобы оно удовлетворяло всем трем условиям формообразования.
• Значение ε, удовлетворяющее первому условию формо- образования, находится из системы неравенств:
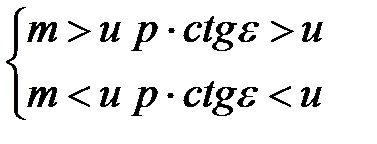 (2.20)
(2.20)
где  .
.

Рисунок 2.7.1 – Влияние угла ψ установки фрезы на ее профиль и определение границ угла ε для спирального сверла: 


В точке В профиля канавки значение параметра u всегда больше, чем в какой-либо другой точке этого профиля. Поэтому, если неравенство (2.20) будет выполнено для точки В, то оно будет выполнено для всех точек профиля канавки (рисунок 2.7).
Таким образом, расчет угла ε по формуле (2.20) следует вести по параметрам профиля канавки в его точке В. Как следует из системы неравенств (2.20), диапазон значений ε (а также - 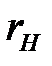 ,так как
,так как  ), удовлетворяющих первому условию формообразования, очень велик:
), удовлетворяющих первому условию формообразования, очень велик:  .
.
• На рисунке 2.7.1 показаны границы  и
и  значений
значений 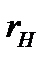 , допустимых для точек В, Е и С профиля канавки вторым условием формообразовани я. Расчет границ
, допустимых для точек В, Е и С профиля канавки вторым условием формообразовани я. Расчет границ  производился по зависимостям уравнений:
производился по зависимостям уравнений:
 (2.21)
(2.21)
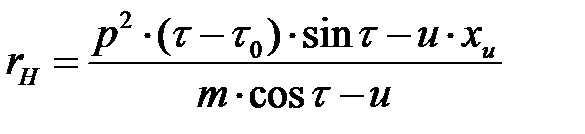 (2.22)
(2.22)
где  ;
;
 ;
;
 ;
;
 ;
;
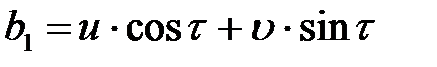 .
.
Для ряда значений угла τ по формулам уравнений (2.21) и (2.22) подсчитываются значения  . Зависимости
. Зависимости 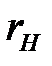 от τ изображаются графиками (рисунок 2.7.2), где точки
от τ изображаются графиками (рисунок 2.7.2), где точки  и
и  пересечения графиков, построенных по уравнениям (2.21) и (2.22) определяют искомые значения
пересечения графиков, построенных по уравнениям (2.21) и (2.22) определяют искомые значения  и
и  .Эти параметры показывают границы значений
.Эти параметры показывают границы значений  , удовлетворяющие первому и второму условиям формообразования винтовой поверхности. При расчете на обычных калькуляторах достаточно построить отрезки графиков по трем-четырем значениям параметра τ. При расчетах на ЭВМ значения
, удовлетворяющие первому и второму условиям формообразования винтовой поверхности. При расчете на обычных калькуляторах достаточно построить отрезки графиков по трем-четырем значениям параметра τ. При расчетах на ЭВМ значения 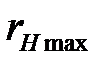 и
и  могут быть определены без построения графиков.
могут быть определены без построения графиков.
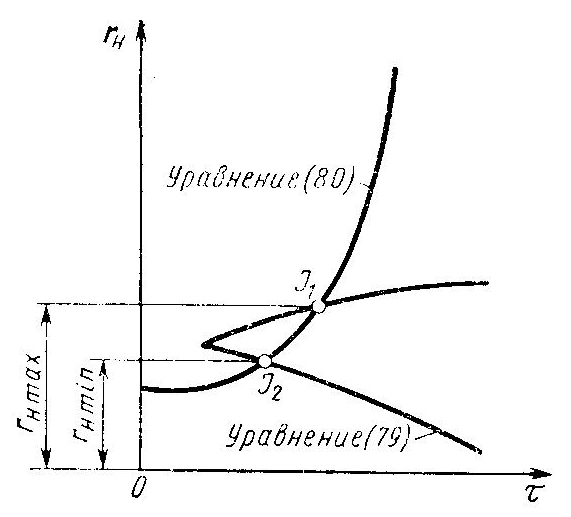
Рисунок 2.7.2 – Графическое решение уравнений (2.21) и (2.22)
Система уравнений (2.21) и (2.22) может давать два корня, один или ни одного. Два корня 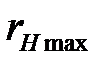 и
и  система дает для большинства участков винтовой поверхности. Для выполнения неравенства
система дает для большинства участков винтовой поверхности. Для выполнения неравенства 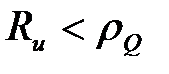 допустимое значение
допустимое значение 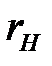 находится между значениями
находится между значениями 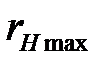 и
и  . Один корень (когда
. Один корень (когда  ) система уравнений (2.21) и (2.22) может давать в двух случаях: во-первых, для одной какой-либо предельной точки криволинейного участка профиля винтовой поверхности и, во-вторых, для точек излома, лежащих во впадине профиля. Отсутствие корней в системе уравнений (2.21) и (2.22) для выпуклых и прямолинейных участков профиля винтовой поверхности указывают на то, что эти участки, безусловно, не будут подрезаться при любых значениях
) система уравнений (2.21) и (2.22) может давать в двух случаях: во-первых, для одной какой-либо предельной точки криволинейного участка профиля винтовой поверхности и, во-вторых, для точек излома, лежащих во впадине профиля. Отсутствие корней в системе уравнений (2.21) и (2.22) для выпуклых и прямолинейных участков профиля винтовой поверхности указывают на то, что эти участки, безусловно, не будут подрезаться при любых значениях 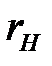 , удовлетворяющих первому условию формообразования. Отсутствие же этих корней для вогнутых участков указывает на то, что при любом значении
, удовлетворяющих первому условию формообразования. Отсутствие же этих корней для вогнутых участков указывает на то, что при любом значении 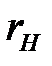 эти участки обработать нельзя.
эти участки обработать нельзя.
Графики этих зависимостей показывают, что для точки В (рисунок 2.7.1г) границы значений 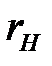 , допустимых вторым условием формообразования, довольно широкие; для точки Е (рисунок 2.7.1в) - они узкие, а для точки С - они отсутствуют, т.к. система уравнений (2.21) и (2.22) не дает действительных корней. Зона значений
, допустимых вторым условием формообразования, довольно широкие; для точки Е (рисунок 2.7.1в) - они узкие, а для точки С - они отсутствуют, т.к. система уравнений (2.21) и (2.22) не дает действительных корней. Зона значений 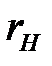 , при которых будет выполнено второе условие формообразования одновременно в точках В и E, определяется значением
, при которых будет выполнено второе условие формообразования одновременно в точках В и E, определяется значением  для точки В и
для точки В и 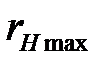 для точки Е (на рисунке она показана штриховыми линиями). Эта зона более узкая, чем зона значений
для точки Е (на рисунке она показана штриховыми линиями). Эта зона более узкая, чем зона значений 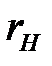 , допускаемых первым условием формообразования. Чем большим будет принято значение
, допускаемых первым условием формообразования. Чем большим будет принято значение 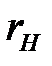 , тем для точек большего участка в зоне точки С не будет выполне но второе условие формообразования.
, тем для точек большего участка в зоне точки С не будет выполне но второе условие формообразования.
• Третье условие формообразования ограничивает выбор параметров m, ε и ψ только для винтовых поверхностей, имеющих на профиле выступы и поднутренные участки. Для остальных участков оно заведомо выполняется при любых значениях параметров m, ε и ψ удовлетворяющих первому условию формообразования. Поэтому фактически проверку значений параметров m, ε и ψ на выполнение третьего условия формообразования приходится проводить сравнительно редко.
• Учитывая сказанное, угол ε рекомендуется определять по формуле (2.20), имея в виду, что а) разность между правой и левой сторонами неравенства (2.20) должна быть больше нуля, чтобы округления при расчетах  и p не смогли нарушить это неравенство; б)
и p не смогли нарушить это неравенство; б)  , допустимый для точки В вторым условием формообразования, несколько больше
, допустимый для точки В вторым условием формообразования, несколько больше  , допустимого первым условием; в) при увеличении разности между правой и левой сторонами неравенства увеличиваются профильные углы в крайних точках профиля фрезы, облегчается выполнение третьего условия формообразования, уменьшается ширина фрезы и затрудняется выполнение второго условия формообразования.
, допустимого первым условием; в) при увеличении разности между правой и левой сторонами неравенства увеличиваются профильные углы в крайних точках профиля фрезы, облегчается выполнение третьего условия формообразования, уменьшается ширина фрезы и затрудняется выполнение второго условия формообразования.
Для практических расчетов рекомендуется угол ε принимать меньше на 2°−4° максимального значения подсчитанного по формуле (2.20).
2.3.4 Расчет параметров RИ, zИ, σ И для точек профиля фрезы
Все расчетные зависимости, необходимые для определения параметров  ,
,  ,
, 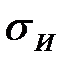 профиля производящей поверхности дискового инструмента, предназначенного для обработки заданной винтовой поверхности, приведены в таблице 2.2.
профиля производящей поверхности дискового инструмента, предназначенного для обработки заданной винтовой поверхности, приведены в таблице 2.2.
Таблица 2.2 – Зависимости для определения параметров  , ,  , , 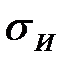 профиля дискового инструмента, предназначенного для обработки винтовой поверхности профиля дискового инструмента, предназначенного для обработки винтовой поверхности
| |
 
| |
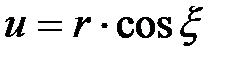
| 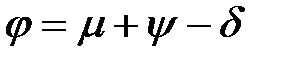
|

| 
|

| 
|
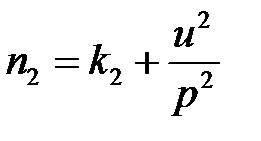
| 
|

| 
|

| 
|

| 
|
При использовании аналитического метода наиболее сложной задачей в решении приведенной системы уравнений является нахождение корней трансцендентного уравнения:
 (2.23)
(2.23)
Данное уравнение позволяет для каждой расчетной точки профиля винтовой поверхности, имеющей параметры r, δ и ξ, определить значение угла τ, соответствующее моменту касания винтовой и производящей поверхностей.
Угол τ (рисунок 2.8) лежит в торцовой плоскости сверла и измеряется между проекциями на эту плоскость оси и касательной к профилю винтовой поверхности, построенной в точке касания последней с производящей поверхностью инструмента.
Примем, что на проекции торцового сечения сверла (рисунок 2.8) положительным будет значение угла τ по часовой стрелке относительно направления оси  .
.

Рисунок 2.8 – Торцовое сечение сверла.
Теоретически винтовая поверхность имеет две стороны: открытую (для контакта с другими деталями машин) и закрытую (обращенную к материалу детали).
Производящая поверхность инструмента должна касаться только с открытой стороны винтовой поверхности. Поэтому при решении уравнения (2.23) знак угла τ для каждой расчетной точки должен быть назначен таким, какой соответствует схеме контакта производящей поверхности с открытой стороной винтовой поверхности. Например, на рисунке 2.7 для всех точек участка BK профиля винтовой поверхности знак параметра τ должен быть минус, а для участка CK – плюс. Положительное значение угла τ может находиться в пределах от 0 до ( ), а отрицательное –
), а отрицательное –
от 0 до ( ).
).
Уравнение (2.23) можно решить методом последовательных приближений, известном в математике под названием метода касательных (метод Ньютона) или методом половинного деления (итерационный метод), решаемым на ЭВМ.
Обозначим левую часть уравнения (2.23) через θ(τ):
 (2.24)
(2.24)
Корнем полученного уравнения будет значение параметра τ, при котором справедливо равенство θ(τ) = 0.
Предлагаемый для решения уравнения (2.23) метод касательныхдает возможность при сравнительно небольшом количестве вычислений отыскать значение искомого корня с желаемой степенью точности. По методу касательных значений  корня в (n+1)-ом приближении подсчитывается по уравнению
корня в (n+1)-ом приближении подсчитывается по уравнению
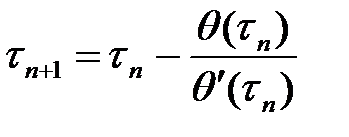 , (2.25)
, (2.25)
где θ(τ) - это значение первой производной функции θ(τ).
 (2.26)
(2.26)
Тогда
 (2.27)
(2.27)
Прежде чем пользоваться формулой (2.23), необходимо выбрать значение τn, с которого можно вести приближение к корню τ. Однако условия приближения к корню зависят от соотношения величин n1, n2, n3 и поэтому вопрос о выборе можно решить только после анализа функции (2.24).
В общем случае (если m ≠ ∞ и ε ≠ 0) график функции θ(τ) изображается отдельными ветвями, причем каждая ветвь (за исключением случая, когда n1 = n2) занимает диапазон значений τ, равный | π |. При значениях τ = - π; 0; + π; функция θ(τ) имеет разрывы (рисунок 2.9). Каждое пересечение оси τ ветвью функции θ(τ) соответствует корню уравнения (2.23). В зависимости от значений параметров r, δ, ξ, p, m, ε, ψ, по которым подсчитываются величины n1, n2, n3, входящие в уравнение (2.23), данная ветвь может пересекать ось или не пересекать ее.
При n2 > n1 график функции θ(τ) имеет вид, показанный на рисунке 2.9 а. Каждая ветвь имеет один корень. Как показывает анализ, корень τ в этом случае будет лежать между величиной arccos n1/n2 и величиной n3.

а) б) в)
Рисунок 2.9 – График функции θ(τ) при: а – n1 > n2;
б – n1 < n2; в – n1 = n2
При n2 < n1 график функции θ(τ) (рисунок 2.9 б) имеет точку максимума (или минимума), и в зависимости от величины n3 уравнение (2.23) имеет два корня (ветвь 1), один корень (два совпавших) (ветвь 2) или ни одного (ветвь 3).
При n2 = n1 график функции θ(τ) имеет одну ветвь
(рисунок 2.9 в), распространяющуюся от τ = - π до τ = + π.
В этом случае уравнение (2.23) имеет только один корень. При n3 < 0 корень τ имеет знак плюс (ветвь 1); при n3 = 0 корень τ = 0 (ветвь 2); при n3 > 0 корень τ имеет знак минус.
2.3.5 Определение параметров ρ, q, t дуг окружностей, очерчивающих профиль фрезы для винтовых канавок сверла
Профиль фрезы для канавки сверла, построенный по рассчитанным координатам Rи и zи,на практике обычно заменяют тремя (реже двумя) дугами окружностей (рисунок 2.10). Поэтому положение и количество расчетных точек на профиле канавки сверла нужно выбирать так, чтобы потом удобнее было построить указанные дуги окружностей. Для случая, когда профиль фрезы заменяется тремя дугами, в качестве расчетных рекомендуется (рисунок 2.6) на формообразующем участке ВК брать три точки: В (r = 0,5 D), F (r = 0,25 D ÷ 0,3 D), К (r = 0,5 d0), а на участке СК одну точку Е (sinα = ρ / L, где α- это некоторый вспомогательный угол). Порядок расчета координат Rи и zи профиля фрезы устанавливается зависимостями таблицы 2.2
Замену теоретического профиля фрезы дугами окружностей удобнее производить по способу, когда каждая дуга окружности строится по двум расчетным точкам и положению касательной к профилю фрезы в одной из них. Как показала практика, точность замены получается выше, если положение этой касательной принять в точке  профиля фрезы. В таблице 2.3 приведены зависимости для расчета радиусов
профиля фрезы. В таблице 2.3 приведены зависимости для расчета радиусов  указанных дуг и координат q и t их центров. Зависимости получены по рисунку 2.10 и предусматривают замену теоретического профиля фрезы дугами окружностей от точки
указанных дуг и координат q и t их центров. Зависимости получены по рисунку 2.10 и предусматривают замену теоретического профиля фрезы дугами окружностей от точки  до точки
до точки  .
.
| Таблица 2.3 – Зависимости для определения параметров ρ, q, t дуг окружностей, очерчивающих профиль фрезы для винтовых канавок сверла | |
| σuF | 
|
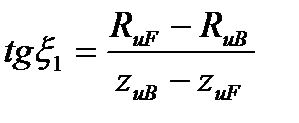
| 
|
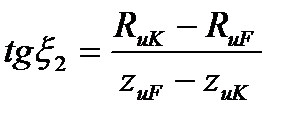
| 
|

| 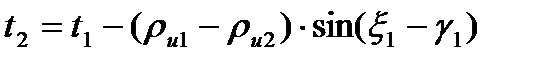
|

| 
|

| 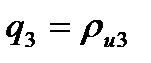
|
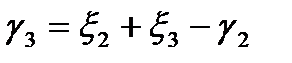
| 
|

| 
|
Неформообразующая часть по обе стороны профиля фрезы определяется профилями поверхностей  . За точкой
. За точкой  профиль поверхности
профиль поверхности 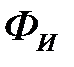 обычно не определяют, а назначают величину перекрытия i, которая устанавливается практически. Перекрытие оформляется отрезком касательной, проведенной в точке
обычно не определяют, а назначают величину перекрытия i, которая устанавливается практически. Перекрытие оформляется отрезком касательной, проведенной в точке  к дуге радиуса
к дуге радиуса  . Угол
. Угол 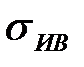 наклона этого отрезка определяется по рисунку 2.10:
наклона этого отрезка определяется по рисунку 2.10:
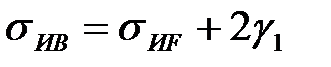 (2.25)
(2.25)
Однако для специальных сверл (с большим значением утла наклона винтовой канавки ω и с очень малыми углами  при вершине режущей части), а также при значениях параметров m, ε, ψ, отличных от рекомендованных, в зоне точки
при вершине режущей части), а также при значениях параметров m, ε, ψ, отличных от рекомендованных, в зоне точки  профиль фрезы надо оформить в зависимости от формы и положения профиля
профиль фрезы надо оформить в зависимости от формы и положения профиля  поверхности
поверхности  , построенной для этой точки. Для определения профиля фрезы за точкой
, построенной для этой точки. Для определения профиля фрезы за точкой  надо знать профиль
надо знать профиль  поверхности
поверхности  на этом участке, построенный для крайней точки С профиля канавки.
на этом участке, построенный для крайней точки С профиля канавки.
Координаты  и
и  профиля поверхности
профиля поверхности  для данной точки (r, δ) профиля винтовой поверхности определяются по зависимостям таблицы 2.2. Для того чтобы воспользоваться этими зависимостями, надо задаться рядом значений координаты z в зоне от
для данной точки (r, δ) профиля винтовой поверхности определяются по зависимостям таблицы 2.2. Для того чтобы воспользоваться этими зависимостями, надо задаться рядом значений координаты z в зоне от  до
до 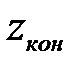 с некоторым шагом
с некоторым шагом  . Для построения профиля поверхности
. Для построения профиля поверхности 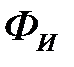 для точки
для точки  эта зона должна располагаться в районе значений координаты
эта зона должна располагаться в районе значений координаты  (угол
(угол  будет известен при расчете координат
будет известен при расчете координат 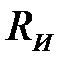 и
и  профиля фрезы для точки В по формулам таблицы 2.2), а для построения профиля поверхности
профиля фрезы для точки В по формулам таблицы 2.2), а для построения профиля поверхности  для точки
для точки  эта зона должна располагаться в районе значений координаты
эта зона должна располагаться в районе значений координаты 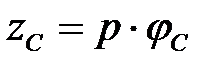 (угол
(угол  будет известен при расчете координат
будет известен при расчете координат  и
и  профиля фрезы для точки С по формулам, приведенным в таблице 2.3.
профиля фрезы для точки С по формулам, приведенным в таблице 2.3.
Участок за точкой  профиля фрезы (рисунок 2.10) должен быть оформлен так, чтобы он не пересекал профиль поверх –
профиля фрезы (рисунок 2.10) должен быть оформлен так, чтобы он не пересекал профиль поверх –
ности  . В этом случае гарантируется выполнение третьего условия формообразования канавки для точки С, и следовательно гарантируется отсутствие подреза профиля канавки в районе
. В этом случае гарантируется выполнение третьего условия формообразования канавки для точки С, и следовательно гарантируется отсутствие подреза профиля канавки в районе
точки С. Участок профиля фрезы за точкой  оформляется прямолинейным отрезком, касательным к дуге радиуса
оформляется прямолинейным отрезком, касательным к дуге радиуса 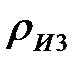 и проводится таким образом, чтобы он не пересекал профиля
и проводится таким образом, чтобы он не пересекал профиля 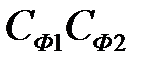 поверхности
поверхности 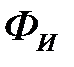 .
.
Однако при некоторых значениях параметров сверла и установки фрезы профиль поверхности  может пересекать дугу радиуса
может пересекать дугу радиуса  и, следовательно, при этом оформленный указанным способом профиль фрезы будет подрезать профиль канавки.
и, следовательно, при этом оформленный указанным способом профиль фрезы будет подрезать профиль канавки.
Если величина подрезания ожидается большой (об этом можно судить по положению профиля  относительно профиля фрезы), то при окончательном оформлении профиля фрезы надо радиус
относительно профиля фрезы), то при окончательном оформлении профиля фрезы надо радиус  заменить радиусом
заменить радиусом  , величину которого назначить такой, чтобы профиль фрезы касался профиля
, величину которого назначить такой, чтобы профиль фрезы касался профиля 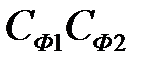 или пересекал его на небольшую величину.
или пересекал его на небольшую величину.
Оформление рабочего профиля фрезы ведется так (рисунок 2.11а): от точки  до точки
до точки  сохраняется профиль, образованный дугами
сохраняется профиль, образованный дугами  и
и  ; от точки
; от точки  очерчивается вершина профиля дугой некоторого радиуса
очерчивается вершина профиля дугой некоторого радиуса  . Выше точки
. Выше точки  профиль оформляется прямой линией, которая проходит по касательной в точке
профиль оформляется прямой линией, которая проходит по касательной в точке  относительно дуги радиуса
относительно дуги радиуса  . Величина радиуса
. Величина радиуса  выбирается такой, чтобы профиль фрезы проходил примерно посредине между дугой радиуса
выбирается такой, чтобы профиль фрезы проходил примерно посредине между дугой радиуса  и профилем
и профилем 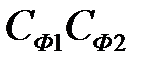 . В этом случае подрез профиля в зоне точки С канавки сверла и «недорез» профиля в зоне точки Е будет иметь вид, показанный на рисунке 2.11б. Граница режущей части профиля фрезы перекрывается величиной прямолинейного отрезка i, которая назначается на основании практических рекомендаций в зависимости от диаметра сверла. Обычно i = 2…4 мм.
. В этом случае подрез профиля в зоне точки С канавки сверла и «недорез» профиля в зоне точки Е будет иметь вид, показанный на рисунке 2.11б. Граница режущей части профиля фрезы перекрывается величиной прямолинейного отрезка i, которая назначается на основании практических рекомендаций в зависимости от диаметра сверла. Обычно i = 2…4 мм.

Рисунок 2.10 – Оформление профиля дискового инструмента для обработки стружечных канавок у спиральных сверл при невыполнении третьего условия формообразования.






